B. Code For 1 分治

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Jon fought bravely to rescue the wildlings who were attacked by the white-walkers at Hardhome. On his arrival, Sam tells him that he wants to go to Oldtown to train at the Citadel to become a maester, so he can return and take the deceased Aemon's place as maester of Castle Black. Jon agrees to Sam's proposal and Sam sets off his journey to the Citadel. However becoming a trainee at the Citadel is not a cakewalk and hence the maesters at the Citadel gave Sam a problem to test his eligibility.

Initially Sam has a list with a single element n. Then he has to perform certain operations on this list. In each operation Sam must remove any element x, such that x > 1, from the list and insert at the same position , , 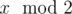 sequentially. He must continue with these operations until all the elements in the list are either 0 or 1.

Now the masters want the total number of 1s in the range l to r (1-indexed). Sam wants to become a maester but unfortunately he cannot solve this problem. Can you help Sam to pass the eligibility test?

Input

The first line contains three integers n, l, r (0 ≤ n < 250, 0 ≤ r - l ≤ 105, r ≥ 1, l ≥ 1) – initial element and the range l to r.

It is guaranteed that r is not greater than the length of the final list.

Output

Output the total number of 1s in the range l to r in the final sequence.

Examples

input

7 2 5

output

4

input

10 3 10

output

5

Note

Consider first example:

这个题目做的挺漂亮嘛!哈哈！

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<vector>
#include<iostream>
#define MAXN 200009
#define eps 1e-11 + 1e-12/2
typedef long long LL;

using namespace std;
/*
显然！分治！
*/
LL n, l ,r;
LL solve(LL x, LL beg,LL end)
{
    LL mid = (beg + end) / 2;
    if (beg == mid) return 1;
    if (r < mid)
        return solve(x / 2, beg, mid - 1);
    else if (l > mid)
        return solve(x / 2, mid + 1, end);
    else
    {
        LL ret = x % 2;
        if (l < mid) ret += solve(x / 2, beg, mid - 1);
        if (r > mid) ret += solve(x / 2, mid + 1, end);
        return ret;
    }
    return 0;
}
int main()
{
    
        cin >> n >> l >> r;
        if (n == 0)
        {
            cout << 0 << endl;
            return 0;
        }
        LL len = pow(2, floor(log2(n)) + 1) - 1;
        cout << solve(n, 1, len) << endl;
}