算法导论--散列表的数学分析(精解)链表法
散列表的具体实现就不多做介绍了,就是一个数组,每个下标存储的是碰撞的元素的链表头指针,如下图所示::

下面直接研究对用链接法散列的分析:
给定一个能存放n个元素的、具有m个槽位的散列表T,定义T的装载因子α为n/m,即一个链中平均存储的元素数。
用链接法散列的最坏情况性能很差:所有的n个关键字都散列到同一个槽中,从而产生出一个长度为n的链表。这时,最坏情况下查找的时间为O(n),再加上计算散列函数的时间,这么一来就和用一个链表来链接所有的元素差不多了。显然我们并不是因为散列表的最坏情况性能差才用它的。
散列方法的平均性态依赖于所选取的散列函数h在一般情况下,将所有的关键字分布在m个槽位上的均匀程度。这会儿我们先假定任何元素散列到m个槽中每一个的可能性是相同的,且与其他元素已被散列到什么位置上是独立无关的。称这个假设为简单一致散列。
对于j=0,1,...,m-1,列表T[j](每个槽位对应的链表)的长度用nj表示,这样有:

nj的平均值为E[nj]=α=n/m。
假定可以在O(1)时间内计算出散列值h(k)(数组下标),从而查找具有关键字为k的元素的时间线性地依赖于表T[h(k)]的长度nh(k)。先不考虑计算散列函数和寻址槽h(k)的O(1)时间,我们来看看查找算法期望查找的元素数,即为比较元素的关键字是否为k而检查的表T[h(k)]中的元素数。分两种情况来考虑。在第一种情况中,查找不成功:表中没有一个元素的关键字为k。在第二种情况中,查找成功地找到关键字为k的元素。
定理11.1 对一个用链接技术来解决碰撞的散列表,在简单一致散列的假设下,一次不成功查找的期望时间为O(1+α)。
证明:在简单一致散列的假设下,任何尚未被存储在表中的关键字k都是等可能地被散列到m个槽的任一个之中。因而,当查找一个关键字k时,在不成功的情况下,查找的期望时间就是查找至链表T[h(k)]末尾的期望时间,这一时间的期望长度为E[nh(k)]=α。于是,一次不成功的查找平均要检查α个元素,所需的总时间(包括计算h(k)的时间)为O(1+α)。
对于成功的查找来说,情况略有不同,这是因为每个链表并不是等可能地被查找到的。某个链表被查找到的概率与它所包含的元素数成正比。然而,期望的查找时间仍然是O(1+α)。
定理11.2 在简单一致散列的假设下,对于用链接技术解决碰撞的散列表,平均情况下一次成功的查找需要O(1+α)时间。
证明:假设要查找的关键字是表中存放的n个关键字中任何一个的可能性是相同的。在对元素x的一次成功的查找中,所检查的元素数比x所在的链表中,出现在x前面的元素数多1。在该链表中,出现在x之前的元素都是在x之后插入的,这是因为新的元素都是在表头插入的。为了确定所查找元素的期望数目,对x所在的链表中,在x之后插入到表中的期望元素数加1,再对表中的n个元素x取平均。设xi 表示插入到表中的第i 个元素,i=1,2,...,n,并设ki=key[xi]。对关键字ki和kj,定义指示器随机变量Xij=I{h(ki)=h(kj)}。在简单一致散列的假设下,有Pr{h(ki)=h(kj)}=1/m,从而根据引理5.1,有E[Xij]=1/m。于是,在一次成功的查找中,所检查元素的期望数目为
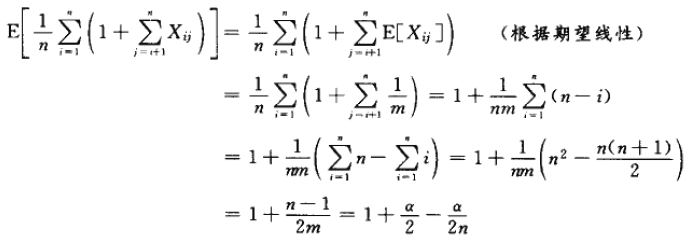
这里有几点注意:
1.根据离散数学,计算一个算法在平均状态下的计算复杂性,可以转变成计算一个随机变量的期望值。设一个实验的样本空间是可能输入aj(j=1,2,...,n)的集合,且令随机变量X对aj 赋值是aj 作为输入时该算法用到的操作次数。基于我们对输入的了解,对每个可能的输入aj 赋给一个概率p(aj)。那么该算法在平均状态下的复杂性是
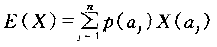
2.根据证明的第一句可知每个可能的输入的概率为1/n。也就是说x等于表中第i 个元素的概率是1/n。
3.指示器随机变量Xij=I{h(ki)=h(kj)}的含义是如果i 和j 散列在同一个槽位当中,也就是在同一个链表中时,加1次。
因此,综上所述,在x之后插入到表中的所检查元素的总数目为:
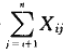
算法在平均状态下的所检查元素的总数目为:
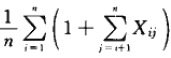
最后再计算这个式子的期望值就能得出所检查元素的期望数目。于是,一次成功的查找所需的全部时间(包括计算散列函数的时间)为O(2+α/2-α/2n)=O(1+α)。



