算法导论--快速排序的离散数学分析
下面是伪代码,这里为了效率更高效,把切分值改成随机化,算法原码请参考 算法-5.快速排序
QUICKSORT(A,p,r) 1 if p<r 2 then q = PARTITION(A,p,r) 3 QUICKSORT(A,p,q-1) 4 QUICKSORT(A,q+1,r) RANDOMIZED-PARTITION(A,p,r) 1 i=RANDOM(p,r) 2 exchange A[r]<->A[i] 3 return PARTITION(A,p,r) PARTITION(A,p,r) 1 x=A[r] 2 i=p-1 3 for j=p to r-1 4 do if A[j]<=x 5 then i=i+1 6 exchange A[i]<->A[j] 7 exchange A[i+1]<->A[r] 8 return i+1
1.最坏情况分析
如果快速排序中每一层递归上所做的都是最坏情况划分,则运行时间为Θ(n2)。从直觉上看,这就是最坏情况运行时间。下面来证明。
利用代换法,可以证明快速排序的运行时间为O(n2)。设T(n)是过程QUICKSORT作用于规模为n的输入上的最坏情况时间,则有:
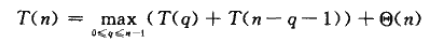 (递归式1)
(递归式1)
其中参数q由0变到n-1,这是因为过程PARTITION产生两个子问题,总的大小为n-1.我们猜测T(n)<=cn2成立,c为某个常数。将此式代入递归式1,得:
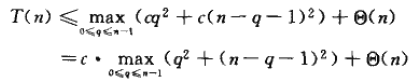
表达式q2+(n-q-1)2在参数的取值区间0<=q<=n-1的某个端点上取得最大值,因为该式关于q的二阶导数是正的(所以原表达式是凹函数,并且当q=(n-1)/2时为最小值)。这样,就有界(取q=0或n-1)


对T(n)就有:
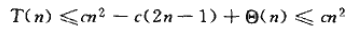
因为我们可以选择足够大的常数c,使得项c(2n-1)能支配Θ(n)。于是,快速排序的(最坏情况)运行时间为Θ(n2)。
2.期望的运行时间(即平均运行时间)
设当QUICKSORT在一个包含n个元素的数组上运行时,PARTITION在第4行中所做比较的总次数为X。那么,QUICKSORT的运行时间为O(n+X)。证明:
根据对PARTITION的调用共有n次。每一次调用都需做固定量的工作,再执行若干次for循环。在for循环的每一轮迭代中,都要执行第4行。
我们的目标是计算出X,即在对PARTITION的所有调用中,所执行的总的比较次数。我们并不打算分析在每一次PARTITION调用中做了多少次比较,而是希望导出关于总的比较次数的一个界。为了达到这一目的,我们必须了解算法在何时要对数组中的两个元素进行比较,何时不进行比较。为了便于分析,我们将数组A的各个元素重新命名为z1,z2,...,zn,其中zi 是数组A中第i个最小的元素。此外,我们还定义Zij={zi, zi+1, ... ,zj}为zi 与zj 之间(包含这两个元素)的元素集合。
那么,算法何时会比较zi 与zj 呢?为了回答这个问题,我们首先观察到每一对元素至多比较一次。这是为什么呢?因为各个元素仅与主元元素进行比较,并且,在某一次PARTITION调用结束之后,该次调用中所用到的主元元素就再也不会与任何其他元素进行比较了。
我们的分析要用到指示器随机变量,我们定义

我们要考虑的是在算法的执行过程中,是否有任何的比较发生,而不是在循环的一次迭代或对PARTITION的一次调用中是否有比较发生。因为每一对元素至多被比较一次,因而,我们可以很容易地刻划算法所执行的总的比较次数:

对上式两边取期望值,再利用期望值的线性特性和引理1,可以得到:


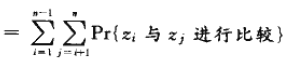
在上式中,Pr{zi 与zj 进行比较}还有待于进一步计算。
一般而言,一旦一个满足zi<x<zj 的主元x被选择后,我们知道,zi 与zj 以后是再也不可能进行比较了。另一方面,如果zi 在Zij 中的所有其他元素之前被选为主元,那么zi 就将与Zij 中的除了它自己以外的所有元素进行比较。类似地,如果zi 在Zij 中其他元素之前被选为主元,那么zj 将与Zij 中除自身以外的每项进行比较。由此我们知道,zi 会与zj 进行比较,当且仅当Zij中将被选作主元的第一个元素是zi 或zj。
我们现在来计算这一事件发生的概率。在Zij中的某一元素被选为主元之前,集合Zij 整个都是在同一划分中的。于是,Zij中的任何元素都会等可能地被首先选为主元。因为集合Zij中共有j-i+1个元素,所以,任何元素被首先选为主元的概率是1/(j-i+1)。于是,我们有:
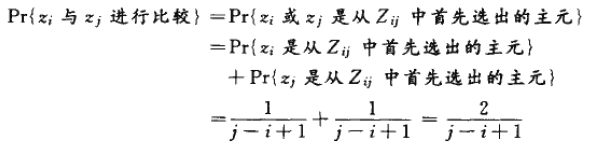
上式中的第二行成立是因为其中涉及的两个事件是互斥的。将等式综合起来,有:

在求这个和式时,可以将变量作个变换(k=j-i),并利用等式1中给出的有关调和级数的界:


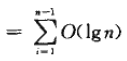

于是,我们可以得出结论,即利用RANDOMIZED-PARTITION,快速排序算法期望的运行时间为O(nlgn)。
引理1:给定样本空间S和S中的事件A,令XA=I{A},则E[XA]=Pr{A}
等式1:




