算法—4.归并排序（自顶向下）

1.基本思想

将两个有序的数组归并成一个更大的有序数组，很快人们就根据这个操作发明了一种简单的递归排序算法：归并排序。要将一个数组排序，可以先(递归地)将它分成两半分别排序，然后将结果归并起来。你将会看到，归并排序最吸引人的性质是它能够保证将任意长度为N的数组排序所需时间和NlogN成正比；它的主要缺点则是它所需的额外空间和N成正比。简单的归并排序如下图所示：

原地归并的抽象方法：

实现归并的一种直截了当的办法是将两个不同的有序数组归并到第三个数组中，实现的方法很简单，创建一个适当大小的数组然后将两个输入数组中的元素一个个从小到大放入这个数组中。

public void merge(Comparable[] a, int lo, int mid, int hi){
		int i = lo, j = mid+1;
		//将a[lo..hi]复制到aux[lo..hi]
		for (int k = lo; k <= hi; k++) {
			aux[k] = a[k];
		}
		//归并回到a[lo..hi]
		for (int k = lo; k <= hi; k++) {
			if(i > mid){
				a[k] = aux[j++];
			}
			else if(j > hi){
				a[k] = aux[i++];
			}
			else if(less(aux[j], aux[i])){
				a[k] = aux[j++];
			}
			else{
				a[k] = aux[i++];
			}
		}
	}

以上方法会将子数组a[lo..mid]和a[mid+1..hi]归并成一个有序的数组并将结果存放在a[lo..hi]中。在归并时（第二个for循环）进行了4个条件判断：左半边用尽（取右半边的元素）、右半边用尽（取左半边的元素）、右半边的当前元素小于左半边的当前元素（取右半边的元素）以及右半边的当前元素大于等于左半边的当前元素（取左半边的元素）。

2.具体算法

/**
 * 自顶向下的归并排序
 * @author huazhou
 *
 */
public class Merge extends Model{
	private Comparable[] aux;	//归并所需的辅助数组

	public void sort(Comparable[] a){
		System.out.println("Merge");
		aux = new Comparable[a.length];	//一次性分配空间
		sort(a, 0, a.length - 1);
	}

	//将数组a[lo..hi]排序
	private void sort(Comparable[] a, int lo, int hi){
		if(hi <= lo){
			return;
		}
		int mid = lo + (hi - lo)/2;
		sort(a, lo, mid);	//将左半边排序
		sort(a, mid+1, hi);	//将右半边排序
		merge(a, lo, mid, hi);	//归并结果
	}
}

　　此算法基于原地归并的抽象实现了另一种递归归并，这也是应用高效算法设计中分治思想的最典型的一个例子。这段递归代码是归纳证明算法能够正确地将数组排序的基础：如果它能将两个子数组排序，它就能够通过归并两个子数组来将整个数组排序。

要对子数组a[lo..hi]进行排序，先将它分为a[lo..mid]和a[mid+1..hi]两部分，分别通过递归调用将它们单独排序，最后将有序的子数组归并为最终的排序结果。

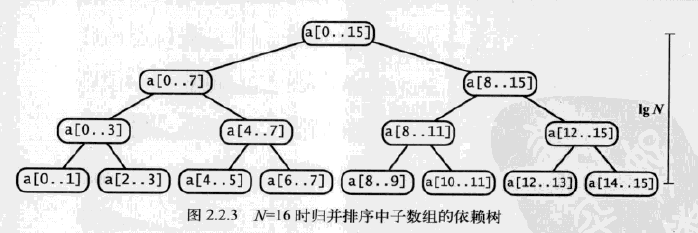
要理解归并排序就要仔细研究该方法调用的动态情况，如下图中的轨迹所示。要将a[0..15]排序，sort()方法会调用自己将a[0..7]排序，再在其中调用自己将a[0..3]和a[0..1]排序。在将a[0]和a[1]分别排序之后，终于才会开始将a[0]和a[1]归并（简单起见，我们在轨迹中把对单个元素的数组进行排序的调用省略了）。第二次归并是a[2]和a[3]，然后是a[0..1]和a[2..3]，以此类推。从这段轨迹可以看到，sort()方法的作用其实在于安排多次merge()方法调用的正确顺序。

3.算法分析

这段代码也是我们分析归并排序的运行时间的基础。我们也可以通过下图所示的树状图来理解命题。每个结点都表示一个sort()方法通过merge()方法归并而成的子数组。这棵树正好有n层（n=4，n为lgN，lg是以2为底）。对于0到n-1之间的任意k，自顶向下的第k层有2^k个子数组，每个数组的长度为2^n-k，归并最多需要2^n-k次比较。因此每层的比较次数为2^kx2^n-k=2ⁿ，n层总共为n2ⁿ=NlgN。

命题：对于长度为N的任意数组，自顶向下的归并排序需要1/2NlgN至NlgN次比较。

证明：令C(N)表示将一个长度为N的数组排序时所需要的比较次数。我们有C(0)=C(1)=0，对于N>0，通过递归的sort()方法我们可以由相应的归纳关系得到比较次数的上限：

C(N)<=C(_└N/2_┘)+C(^┌N/2^┐)+N

右边的第一项是将数组的左半部分排序所用的比较次数，第二项是将数组的右半部分排序所用的比较次数，第三项是归并所用的比较次数。因为归并所需的比较次数最少为_└N/2_┘，比较次数的下限是：

C(N)>=C(_└N/2_┘)+C(^┌N/2^┐)+_└N/2_┘

当N为2的幂（即N=2ⁿ）且等号成立时我们能够得到一个解。首先，因为_└N/2_┘=^┌N/2^┐=2^n-1，可以得到：

C(2ⁿ)=2C(2^n-1)+2ⁿ

将两边同时除以2ⁿ可得：

C(2ⁿ)/2ⁿ=C(2^n-1)/2^n-1+1

用这个公式替换右边的第一项，可得：

C(2ⁿ)/2ⁿ=C(2^n-2)/2^n-2+1+1

将上一步重复n-1遍可得：

C(2ⁿ)/2ⁿ=C(2⁰)/2⁰+n

将两边同时乘以2ⁿ就可以解得：

C(N)=C(2ⁿ)=n2ⁿ=NlgN

对于一般的N，得到的准确值要更复杂一些。但对比较次数的上下界不等式使用相同的方法不难证明前面所述的对于任意N的结论。这个结论对于任意输入值和顺序都成立。

 

命题：对于长度为N的任意数组，自顶向下的归并排序最多需要访问数组6NlgN次。

证明：每次归并最多需要访问数组6N次（2N次用来复制，2N次用来将排好序的元素移动回去，另外最多比较2N次），根据上面的命题即可得到这个命题的结果。

4.总结

两个命题告诉我们归并排序所需的时间和NlgN成正比。这和之前所述的初级排序方法不可同日而语，它表明我们只需要比遍历整个数组多个对数因子的时间就能将一个庞大的数组排序。可以用归并排序处理数百万甚至更大规模的数组，这是插入排序或者选择排序做不到的。归并排序的主要缺点是辅助数组所使用的额外空间和N的大小成正比。

再来看看乱序和部分有序的情况：

public static void main(String[] args) {
		// TODO Auto-generated method stub
		int[] model = {6,4,1,5,2,3,9,7,8};
		int size = 1000000;
		int[] array = new int[size];
		for (int i = 0; i < array.length; i++) {
			array[i] = model[i%model.length];
			if(size <= 1000){
				System.out.print(array[i]);
			}
		}
		System.out.println("");
		double start_random = System.currentTimeMillis();
		merge_sort(array);
		double end_random = System.currentTimeMillis();
		for (int i = 0; i < size; i++) {
			if(size <= 1000){
				System.out.print(array[i]);
			}
		}
		System.out.println("size is " + size);
		System.out.println("\nrandom sort spend times:" + (end_random - start_random)/1000 + "s");
		array[size/2] = 0;
		double start_partsortted = System.currentTimeMillis();
		merge_sort(array);
		double end_partsortted = System.currentTimeMillis();
		for (int i = 0; i < size; i++) {
			if(size <= 1000){
				System.out.print(array[i]);
			}
		}
		System.out.println("\npartsortted sort spend times:" + (end_partsortted - start_partsortted)/1000 + "s");
	}

百万级

千万级

归并排序是一种稳定的排序，但不是就地排序，如果用单链表作存储结构，很容易给出就地的归并排序。

【源码下载】