算法—比较两种排序算法:选择排序和插入排序(详细)
现在我们已经实现了两种排序算法,我们很自然地想知道选择排序和插入排序哪种更快。这里我们第一次用实践说明我们解决这个问题的办法。
性质:对于随机排序的无重复主键的数组,插入排序和选择排序的运行时间是平方级别的,两者之比应该是一个较小的常数。
例证:这个结论在过去的半个世纪中已经在许多不同类型的计算机上经过了验证。在1980年本书第一版完成之时插入排序就比选择排序快一倍,现在仍然是这样,尽管那时这些算法将10万条数据排序需要几个小时而现在只需要几秒钟。在你的计算机上插入排序也比选择排序快一些吗?可以通过SortCompare类来检测。它会使用由命令行参数指定的排序算法名称所对应的sort()方法进行指定次数的实验(将指定大小的数组排序),并打印出所观察到的各种算法的运行时间的比例。
我们使用Stopwatch来计时。
随机数组的输入模型由SortCompare类中的timeRandom-Input()方法实现。这个方法会生成随机的Double值,将它们排序,并返回指定次测试的总时间。
用命令行参数指定重复次数的好处是能够运行大量的测试(测试次数越多,每遍测试所需的平均时间就越接近于真实的平均数据)并且能够减小系统本身的影响。
/**
* 比较两种排序算法
* @author huazhou
*
*/
public class SortCompare {
public static double time(String alg, Comparable[] a){
Selection selection = new Selection();
Insertion insertion = new Insertion();
Stopwatch timer = new Stopwatch();
if(alg.equals("Selection")){
selection.sort(a);
}
if(alg.equals("Insertion")){
insertion.sort(a);
}
return timer.elapsedTime();
}
public static double timeRandomInput(String alg, int N, int T){
//使用算法1将T个长度为N的数组排序
double total = 0.0;
Double[] a = new Double[N];
for (int t = 0; t < T; t++) {
//进行一次测试(生成一个数组并排序)
for (int i = 0; i < N; i++) {
a[i] = StdRandom.uniform();
}
total += time(alg, a);
}
return total;
}
public static void main(String[] args){
String alg1 = args[0];
String alg2 = args[1];
int N = Integer.parseInt(args[2]);
int T = Integer.parseInt(args[3]);
double t1 = timeRandomInput(alg1, N, T);//算法1的总时间
double t2 = timeRandomInput(alg2, N, T);//算法2的总时间
StdOut.printf("For %d random Doubles\n %s is", N, alg1);
StdOut.printf(" %.1f times faster than %s\n", t2/t1, alg2);
}
}
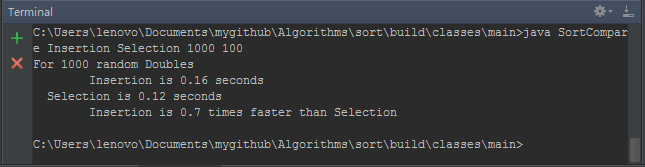
这个用例会运行由前两个命令行参数指定的排序算法,对长度为N(由第三个参数指定)的Double型随机数组进行排序,元素值均在0.0到1.0之间,重复T次(由第四个参数指定),然后输出总运行时间的比例。如Insertion is 0.16 seconds,0.16为重复100次的总运行时间。
下面是对大部分有序的比较(源码没提供下载):
public static void main(String[] args) {
// TODO Auto-generated method stub
int[] model = {6,4,1,5,2,3,9,7,8};
int size = 10;
int[] array = new int[size];
for (int i = 0; i < array.length; i++) {
array[i] = model[i % model.length];
if(size <= 1000){
System.out.print(array[i]);
}
}
System.out.println("");
double start_random = System.currentTimeMillis();
insertion_sort(array);
double end_random = System.currentTimeMillis();
for (int i = 0; i < size; i++) {
if(size <= 1000){
System.out.print(array[i]);
}
}
System.out.println("\nrandom sort spend times:" + (end_random - start_random)/1000 + "s");
array[size/2] = 0;
double start_partsortted = System.currentTimeMillis();
insertion_sort(array);
double end_partsortted = System.currentTimeMillis();
for (int i = 0; i < size; i++) {
if(size <= 1000){
System.out.print(array[i]);
}
}
System.out.println("\npartsortted sort spend times:" + (end_partsortted - start_partsortted)/1000 + "s");
}
/**
* size=十万
* random sort spend times:3.681s
partsortted sort spend times:3.567s
* size=百万
* random sort spend times:463.469s
partsortted sort spend times:395.474s
*/
private static void select_sort(int[] a) {
int N = a.length;
for (int i = 0; i < N; i++) {
int min = i;
for (int j = i+1; j < N; j++) {
if(less(a[j], a[min])){
min = j;
}
}
exch(a, i, min);
}
}
/**
* size=十万
* random sort spend times:4.532s
partsortted sort spend times:0.001s
size=百万
random sort spend times:507.206s
partsortted sort spend times:0.002s
*/
private static void insertion_sort(int[] a){
int N = a.length;
for (int i = 1; i < N; i++) {
for (int j = i; j > 0&&less(a[j], a[j-1]); j--) {
exch(a, j, j-1);
}
}
}
///////////////////
private static boolean less(int x, int y){
if(x < y){
return true;
}
return false;
}
private static void exch(int[] a, int i, int j){
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
关键代码在于
array[size/2] = 0;
将已经排序好的数组正中间的数字改成乱序。从运行结果可以看出,当size为100万时,选择排序对乱序和部分有序的时间差别不大,分别是463秒和395秒;而插入排序对部分有序的排序时间为0.002秒。这也就是前文所说为什么在大部分有序的情况下插入排序是效率最高的算法。
【源码下载】





