动态规划(DP)笔记(三)：常见普通题型

目录

• 坐标型&双序列型
• 划分型
• 状态压缩型

---

坐标型&双序列型

• 特点： 两者都是给的二维输入

  • 双序列型给两个序列

    • 如给定两个字符串序列进行字符匹配：“abc” 与 “abcdefg”，每一个序列对应一个坐标轴：

      

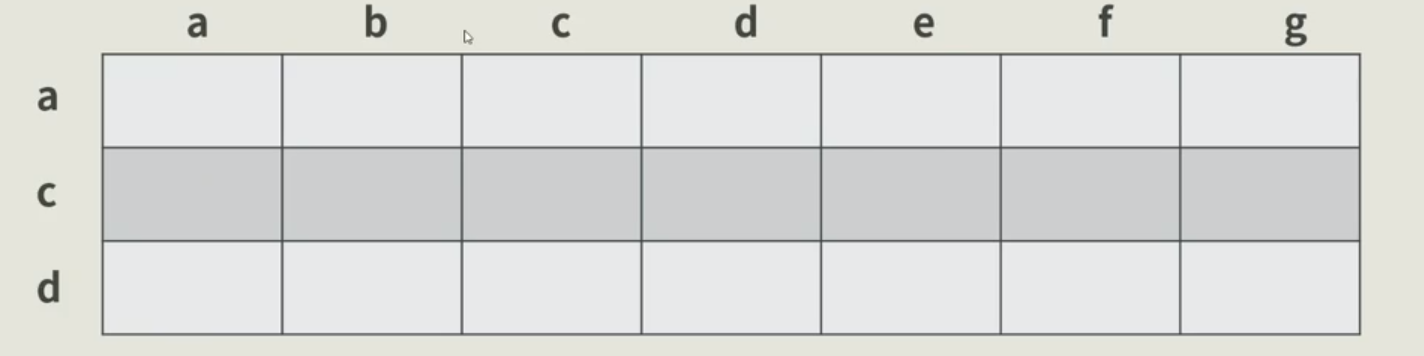
  • 坐标型给坐标：状态转移对应着表格中坐标的移动

• 例题

  leetcode 62. 不同路径

  

  1. 分析

     • 状态表示：使用二维变量 dp[i][j] 表示机器人走到当前位置的路径数
     • 状态转移：机器人自能往右或往下移动，采用被动表示，当前位置的可能路径数为从左侧和上侧的路径数的和 dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
     • 边界：考虑到第一行 dp[0][j] 和第一列 dp[i][0] 只能来自左 / 上侧，故其路径数为 1，即 dp[0][j] = dp[i][0] = 1

  2. 实现

     class Solution {
     public:
         int uniquePaths(int m, int n) {
             int dp[n + 1][m + 1];
             memset(dp, -1, sizeof(dp));
     
             for(int i = 0; i < n; ++i)      //初始化 dp[i][0]
                 dp[i][0] = 1;
     
             for(int j = 1; j < m; ++j)      //初始化 dp[0][j]
                 dp[0][j] = 1;
             
             for(int i = 1; i < n; ++i) {
                 for(int j = 1; j < m; ++j) {
                     dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                 }
             }
     
             return dp[n - 1][m - 1];
         }
     };
     

  leetcode 1143. 最长公共子序列

  

  1. 分析

     • 状态表示：dp[i][j] 表示 text1 的前 i 位 和 text2 的前 j 位的最大字串长度。

     • 状态转移： 当 text1 的第 i+1 位与 text2 的第 j+1 位相同时，最大子序列长度为前 i、j 的最大子序列长度加1；若不等时，最大子序列长度为前 i+1、j 和前 i、j+1 最大子序列长度的最大值，即：

       \[dp[i + 1] [j+1]= \begin{cases} dp[i] [j] + 1& \text{text1[i + 1] = text2[j + 1]} \\ max(dp[i] [j + 1], dp[i + 1] [j])& \text{text1[i + 1] $\neq$ text2[j + 1]} \end{cases} \]

     • 边界：dp[i][0] 和 dp[0][j] 均为 0，表示仅有一个序列时，公共子长度为 0

  2. 实现

     class Solution {
     public:
         int longestCommonSubsequence(string text1, string text2) {
             int row = text1.size(), col = text2.size();
             int dp[row + 1][col + 1];
             memset(dp, 0, sizeof(dp));
     
             for(int i = 1; i <= row; ++i) {
                 for(int j = 1; j <= col; ++j) {
                     if(text1[i - 1] == text2[j - 1])
                         dp[i][j] = dp[i - 1][j - 1] + 1;
                     else
                         dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                 }
             }
             return dp[row][col];
         }
     };
     

---

划分型

• 特点： 将序列不重不漏划分为若干段

• 思路：

  • 状态：dp[i] 表示考虑了序列前 i 个元素的答案
  • 状态转移：先枚举 dp[i]，然后考虑将序列 [i + 1, j] 接在后面自成一段，使其满足条件，然后转移到状态 dp[j]

• 例题

  [leetcode 132. 分割回文串 II]

  

  1. 分析： 要求最少的分割次数，相当于分割为最小段数 - 1

     • 状态表示： dp[i] 表示字符串 s 的前 i 个字符分割的最小段数
     • 状态转移：dp[i] = min( dp[j] ) + 1 且 s[j + 1, i] 也是回文段，(j < i)
     • 边界： dp[0] = 0，当前串长为 0，分割的最小段数为 0

  2. 实现

     class Solution {
     public:
         bool checkPalindrome(int l, int r, string s) {     //[l ... r]
             for(int i = l; i <= r; ++i)
                 if(s[i - 1] != s[r + l - i - 1]) return false;
     
             return true;
         }
         
         int minCut(string s) {
             int len = s.size();
             int dp[len + 1];
             memset(dp, -1, sizeof(dp));
             dp[0] = 0;
     
             for(int i = 1; i <= len; ++i) {
                 for(int j = 0; j < i; ++j) {
                     if(dp[j] == -1 || !checkPalindrome(j + 1, i, s))
                         continue;
                     if(dp[i] == -1 || dp[i] > dp[j] + 1)
                         dp[i] = dp[j] + 1;
                 }
             }
             
             return dp[len] - 1;
         }
     };
     

---

状态压缩

• 特点： 使用一个数的二进制形式保存状态，把二进制转化为十进制从而达到状态压缩

• 位运算的常用操作：

  • 判断 j 为是否为1：(bits >> j)&1
  • 将第 j 位变为1：bits | (1 << j)
  • 将第 j 位变为0：bits & ~(1 << j)

• 例题

  leetcode 1349. 参加考试的最大学生数

  1. 分析&实现

     这题我也不会 ——> B站看这，16:43处

---

参考

动态规划 · 二 - 坐标、双序列、划分 & 状态压缩