KMP算法个人感悟
既然来到了这，那也一定是被KMP困惑了一阵的小伙伴。虽然这篇文章也不一定让你能看懂，但是这算是我自己个人对于KMP的最直接的理解，也许不好，也许有误，望大佬指出。
对于串的模式匹配的算法很多，当然最简单就是暴力破解法（也即是BF算法），由此我们从这开始引入
BF算法原理就是将主串和模式串依次进行比较，若遇到不同的时候，主串和模式串都会回溯（也许开始这会有点迷，但是没影响，后面自然会理解）
如
我们将模式串和主串开始依次比较，第一个都不相同，很简单的就是直接用模式串和第一个和主串的第二个开始比较，如下
就这样依次比较，我们会发现前四个都是不行的（包括其中的一个括号），因此我们就直接从第五个开始比较
我们会发现从模式串的A到B都是相同的，所以直接跳过到不同的位置比较时吧
这是主串和模式串已经出现了不同，于是我们要开始考虑下一步怎么做。
很容易就会想到我们再拿模式串的第一个和主串刚才最开始比较的地方的下一个重新开始比较，如下
这一步的这个过程就叫做回溯
但是我们会发现一个问题因为我们开始匹配成功时已经就确定了前面的位置的字母了，我们将主串回溯和模式串的开头重新比较肯定会失败，这就会浪费很多的时间。那我们仔细的观察就会发现，当我们匹配失败后可以直接将模式串的第三个和主串失配的位置重新开始比较，这样就不用回溯主串的指针了，也不用将模式串的指针回溯到头了，可以节约不少时间。这也就是KMP算法的思路。
但是为什么要从模式串的第三个位置开始比较呢？
我们想想这幅图
当我们匹配到这个地步了，发现不匹配，相当于我们前面的匹配成功的主串是和模式串相同的，也就是说我们是知道了这一部分主串的样子的，我们确切的知道它们每个位置的字符，因此肯定不会去拿一个不一样的字符去比较，这就是浪费时间的作为。所以我们就会寻找其中相同的子串，并根据这个将模式串指针回溯到合适的位置进行比较。
如上面这中情况，我们肯定就会从模式串的第三个位置开始比较，因为我们会发现前面的部分其中有前缀AB和后缀AB是相同，因此如下图
KMP算法
到了这里，我们就可以认真的分析KMP算法的步骤了
首先，我们会将模式串和主串依次比较
然后，若我们遇到了匹配失败的时候，就保持主串的指针不动，尽可能的将模式串向右滑动（即回溯模式串的指针i），回溯到哪里呢就要看后面的next数组，即回溯到对应的next数组的值那里
最后，直到匹配成功或者主串长度不够匹配失败
那么就还有最后一个也是最重要的一个问题了：匹配失败的时候到底将i回溯到哪个位置，怎么计算，计算机肯定不会像我们大脑那么去思考，所以需要我们告诉它
注意：本文接下来的数组相关的是由严老的为准，即数组的第一个位置不存放元素（应该很多人也都是用的这个教材）
我们解决这个回到哪里的问题，我们发现我们思考的时候是找到了前后缀的最长公共元素长度，那我们就来思考如何寻找这个，然后告诉计算机不就行了吗
注：这里的前后缀表示是小于串本身长度的
举例：
对于一个串ABABC
开始寻找
A--0
AB--0
ABA--1
ABAB--2
ABABC--0
就会得到这么一个公共最长前后缀的表
但是这也会有一些不对，例如我们匹配到了C这一步失配，这个表会让我们再次从0开始比较，但这显然不对，因为前面都是AB，因此我们应当从第三个开始比较，所以KMP算法基于这个表做了操作，也就形成了大家所知的next数组
next数组
对于next数组，我们第一个元素肯定是为0，第二个元素是为1（先别疑惑，听我慢慢道来）（当然再提醒一下这里的数组是从1号位置开始存放数据的）
大家想想，若当前的主串比较的位置和模式串的第一个位置都不匹配怎么办？当然BF是直接将主串指针j后移，然后比较。但KMP算法的描述里失配时j时保持不动的，模式串指针i回溯。因此由于第一个元素里面值为0，所以i会等于0，但是0号位置并没有元素，因此当i=0时我们就将j和i都后移一位，是不是就相当于j直接向后移一位了呢。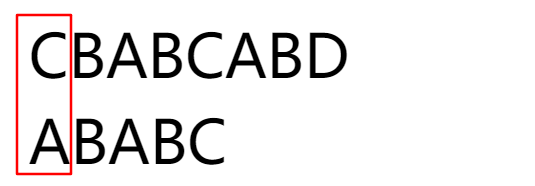 
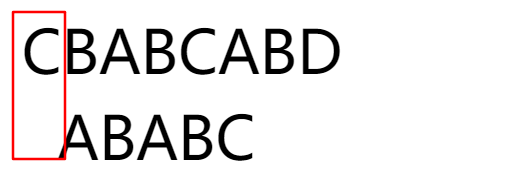
那么第二位为什么一定为1呢？
不妨我们再来假设一下，如果第二位时匹配失败我们应该怎么做呢？其实也就很简单了，我们就保持主串不动，将模式串再从1开始比较起走，因此第二位肯定为1
那么整个next数组怎么求呢？
其实到了这里就很简单了，我们已经明确了第一位和第二位是0和1，那么从第三位开始，值就是前面的最长公共前后缀长度+1
例如
好了，大致的KMP算法内容也就讲到这里了，感谢您看到了这里，如果你觉得还是云里雾里，请你不要质疑你自己，这肯定是我的错。
蟹蟹
