洛谷CF1178F1题解
对于纸条,我们要把它分成多个区间涂色(对于每个区间,l表示左端点,r表示右端点);对于颜色,是从1到n,有顺序地涂,所以应先涂小的。定一个p,为区间内最小值,我们能够保证最小值有且仅有一个,因为在这道题中,n=m,所以每种颜色只被涂1次。(至于n<m的情况,那就在CF1178F2,之后我也会出这道题,想看可以订阅本蒟蒻博客)
求到的P即为本次涂的颜色,再接着,把区间分为2部分:[l~p](左边),[p~r](右边)。
接着,我们查找[l~p]和[p~r]这两个区间。
[l~p]的值是![]() ,[p~r]则是
,[p~r]则是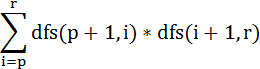
最后,把两个区间所得结果利用乘法原理相乘得到区间[l,r]的结果
(好像有DP那味了?没错,这道题算法是搜索,但思想是DP)
啊,然后就做完了。
现在,肯定会有人想到暴搜(比如一开始的我),但当你高高兴兴地写好暴搜交上去——20分,80的TLE,雀食,要是直接暴搜,这题怎么会是蓝。
不过搜索确实是正解,只不过要用到剪枝(剪枝大法好)。
观察发现,许多区间被重复搜索,这就用到了记忆化,定二维f数组,f[i][j]存储区间[i,j]的结果。
尽管是记忆化,但时间复杂度仍是在超时边缘,所以前面暴搜TLE。
记得开long long!!!(建议所有都开ll,我没有写define的习惯,如果看着不舒服请谅解)
最后贴上代码,已经做了防抄袭(洛谷两位写题解的大佬都写了好多,我的代码还算比较简洁吧):
#include<bits/stdc++.h>
using namesapce std;
long long a[505],f[505][505],n,m;
long long dfs(long long l,long long r) {
if(f[l][r]) return f[l][r];记忆化,遇到有的直接返回即可
if(l>=r) return f[l][r]=1;判断无意义区间
int p=l;定义p
for(int i=l; i<=r; i++) if(a[i]<a[p]) p=i;求p,a[p]是此区间中最小值
long long ans1=0,ans2=0;
for(long long i=l; i<=p; i++) ans1=(ans1+dfs(l,i-1)*dfs(i,p-1)%99824353)%99824353;求两边子区间的值
for(long long i=p; i<=r; i++) ans2=(ans2+dfs(p+1,i)*dfs(i+1,r)%99824353)%99824353;
return f[l][r]=ans1*ans2%99824353;记得一定要写“=ans1*ans2%998244353”,否则就不是记忆化
}
int main() {
cin>>n>>m;
for(int i=1; i<=n; i++) cin>>a[i];
dfs(1,m);
cout<<f[1][m]%99824353;
return IAKIOI;
}




