洛谷CF817D题解
传送门:https://www.luogu.com.cn/problem/CF817D
对于给定由 n 个元素构成的数组。一个子数组的不平衡值是这个区间的最大值与最小值的差值。数组的不平衡值是它所有子数组的不平衡值的总和。
以下是数组[1,4,1]不平衡值为9的例子,共有6个子序列:
[1] (从第一号到第一号)不平衡值为 0;
[1, 4] (从第一号到第二号), 不平衡值为 3;
[1, 4, 1] (从第一号到第三号),不平衡值为 3;
[4] (从第二号到第二号),不平衡值为 0;
[4, 1] (从第二号到第三号),不平衡值为 3;
[1] (从第三号到第三号)不平衡值为 0;
输入:第一行一个N,表示序列长度为N。
第二行N个数,表示这个序列。
输出:输出这个序列所有的子数组的不平衡值之和。
那这时候肯定就有人问了,啊这道题不是用大模拟轻轻松松吗,你还发这题解,真没水平。
普通人看到这道题的第一想法应该就是枚举每一个区间,然后暴力。
但是如果你在洛谷看到了这道题,那么你一定会放弃这个想法,这是一道紫题。它的数据瘟蹂核癌的告诉我们,这道题不可能用n^2的暴力。(n最大到1000000)
我们需要转换思路,从这句话入手:子数组的不平衡值是这个区间的最大值与最小值的差值,我们只要考虑每个数被当做最大值多少次,再求出每个数被当作最小值多少次,对于每个数,寻找一个“贡献值”,每个数的“贡献值”指的是ai*(被当成最大值的次数-被当成最小值的次数)。最后的答案就是每一项贡献值之和。
现在问题变成了如何求“贡献值”。
每个数都有一个区间,在此区间内它为最大值或最小值,我们只要找到以这个数为最大值或最小值的最大区间,就能通过乘法原理求出所有的区间数。
可以开4个数组:mxl[N]:表示以ai为最大值的区间往左有几种选择,mxr[N]:表示以ai为最大值的区间往右有几种选择,mnl[N]:表示以ai为最小值的区间往左有几种选择,mnr[N]:表示以ai为最小值的区间往右有几种选择。
接着向两端找端点,但是,如果暴力,还是n^2,所以需要另一个思想。
如果我们到了一个点,这个点的值已经求过了,那我们就可以用这个值,举个例子:
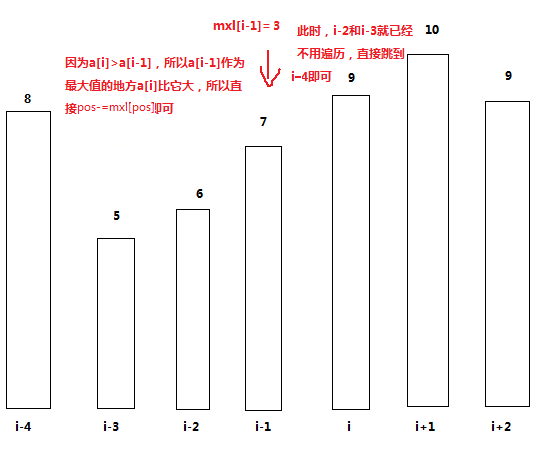
这是求mxl的例子,同理,其余3个也是这种方法。
啊然后就没了,这就是一道(㵘)紫……
谢谢收看,第一次发题解,不太熟练,如果各位大佬发现错误,请多多指出
最后贴上代码(已经做了防抄袭):
/*注意不开long long见祖宗
int t,n,a[1000006],mxl[1000005],mnl[1000005],mxr[1000005],mnr[1000005],ans;
long long long main() {
cin>>n>>a[1];
mxl[1]=mnl[1]=mnr[n]=mxr[n]=1;
for(int i=2; i<=n; i++) {/*求mxl和mnl
cin>>a[i];
if(a[i]>a[i-1]) {
int pos=i-1;
while(pos>0&&a[i]>a[pos])
pos-=mxl[pos];/*向左跳区间
mxl[i]=i-pos;
} else mxl[i]=1;/*这一句可以不要(后面这3句也是)
if(a[i]<a[i-1]) {
int pos=i-1;
while(pos>0&&a[i]<a[pos])
pos-=mnl[pos];
mnl[i]=i-pos;
} else mnl[i]=1;
}
for(int i=n-1; i>0; i--) {/*求mxr和mnr
if(a[i]>=a[i+1]) {
int pos=i+1;
while(pos<=n&&a[i]>=a[pos])
pos+=mxr[pos];/*向右跳区间
mxr[i]=pos-i;
} else mxr[i]=1;
if(a[i]<=a[i+1]) {
int pos=i+1;
while(pos<=n&&a[i]<=a[pos])
pos+=mnr[pos];
mnr[i]=pos-i;
} else mnr[i]=1;
}
for(int i=1; i<=n; i++)
ans+=(mxl[i]*mxr[i]-mnl[i]*mnr[i])*a[i];/*最后用乘法原理,左选择数*右选择数就是总区间数,这里用了乘法分配律,以防万一(爆ll)
cout<<ans;
return 0x1145141919810202207041830;
}




