首先我先介绍一下关于BST树,BST树又称搜索二叉树,即任意节点的左节点肯定比该节点小,右节点比该节点大。所以当中序遍历的时候,你会惊奇的发现遍历的val竟然是从小到大排序的。
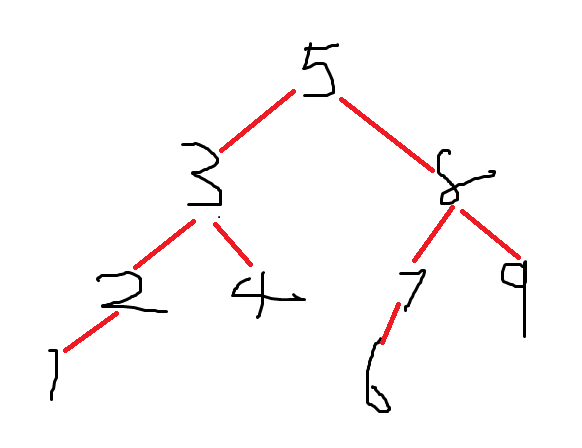
如图就是BST树,先序是5 3 2 1 4 8 7 6 9,中序是1 2 3 4 5 6 7 8 9。知道先序序列后,其实进行对先序sort一下其实就可以得到中序了。所以如果已知是BST树,在知道一个先序或者后序我们便可以构建出唯一的一颗树了。其实我们可以对先序的理解就是每次对树的插入,所以我们可以用以下代码进行某一节点的插入:
Node* Insert(Node* node,int val) { if(node==NULL) { node = new Node(); node->val = val; return node; } if(val < node->val) node->left = Insert(node->left,val); else if(val > node->val) node->right = Insert(node->right,val); return node; }
知道BST的先序序列构树后,如何已知后序如何构树呢,是的还是用以上代码,但是两者不同之处用下面的伪代码进行说明:
pre[n]是先序,post[n]是后序 已知先序构树 Node* root = NULL; for(int i=0;i<n;++i) root = Insert(root,pre[i]); //已知后序构树 for(int i=n-1;i>=0;--i) root = Inert(root,post[i]);
是不是很神奇,两者只需要反一下就行了。为什么呢?我们从上图的3 5 8节点来讲,先序是5 3 8,这是我们知道5是父节点,由于3节点比5小,所以3是左节点,8则是右节点。由于先序是 根 左 右的结构,如果改成根右左的结构呢,此时序列就变成了5 8 3,父节点还是5,左节点还是3,右节点还是8。所以只要保证根节点肯定在左右节点前面就行了。所以如果你把后序序列反转后,你会发现它就是根右左的结构,此时其实对构树还是无影响的。因为构树的左右节点是由中序控制的。
接下来我们要做得是如何把这个算法用到普通二叉树中呢。这时候我们需要知道如何把普通二叉树转换成搜索二叉树。
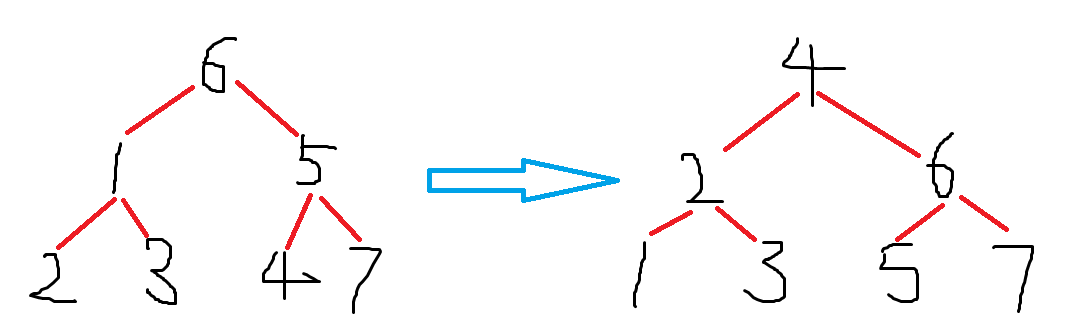
如何把作图转换成右图呢,此时就要用到map来映射了。刚开始我们知道中序排序 2 1 3 6 4 5 7,右边的中序是1 2 3 4 5 6 7,此时我们可以做一个映射,map[左边] = 右边编号。即map[2] = 1,map[1]=2,map[3] = 3,map[6]=4....当这个映射做完后,我们可以在遍历先序或者后序时,把val从根节点开始插入时,如果map[val]比当前节点的对应编号map[node->val]小,说明在左边,不然就在右边。
以下就是关于 二叉树已知先序或者后序,与中序构树的代码:
#include<iostream> #include<cstring> #include<cstdio> #include<map> #include<vector> #include<algorithm> using namespace std; struct Node { int val; Node* left; Node* right; Node(){left = right=NULL;} }; map<int,int> valtoid; Node* Insert(Node* node,int val) { if(node==NULL) { node = new Node(); node->val = val; } else if(valtoid[val]<valtoid[node->val]) node->left = Insert(node->left,val); else node->right = Insert(node->right,val); return node; } void pre_travel(Node* node) { if(NULL==node) return; printf("%d ",node->val); pre_travel(node->left); pre_travel(node->right); } void post_travel(Node* node) { if(NULL==node) return; post_travel(node->left); post_travel(node->right); printf("%d ",node->val); } int main() { int n; scanf("%d",&n); //输入个数 vector<int> vn; //先序或者后序 for(int i=0;i<n;++i) { int val; scanf("%d",&val); vn.push_back(val); } //reverse(vn.begin(),vn.end()); //如果是后序,就反转 for(int i=0;i<n;++i) //输入中序 { int a; scanf("%d",&a); valtoid[a] = i; } Node* root = NULL; cout<<"先序:"; for(int i=0;i<n;++i) root = Insert(root,vn[i]); pre_travel(root); puts(""); cout<<"后序:"; post_travel(root); puts(""); } /* //后序,中序 11 7 6 3 5 20 4 24 21 10 1 9 7 6 5 3 9 4 20 1 10 24 21 //先序,中序 11 9 5 6 7 3 1 4 20 10 21 24 7 6 5 3 9 4 20 1 10 24 21 */


