8-28练习报告
又是颓废的一天! (๑¯◡¯๑)
同机房dalao出了题的比赛,怎能不打?但也只写了两题,第一题都不会写。。
把写了的题的报告就发一发吧。
T3.Ancestor 先辈
题目大意:给出一个长度为\(n\)的序列和\(m\)次操作:\((n,m\le10^5)\)
-
操作一:将区间\(\begin{bmatrix}l\sim r\end{bmatrix}\)加上\(x\)
-
操作二:查询区间\(\begin{bmatrix}l\sim r\end{bmatrix}\)是否为单调不下降序列
还是比较水的,一眼看出可以用线段树维护一段区间是否为单调不下降序列,如果相邻的两个序列都为单调不下降序列,则比较相接处的两个数是否满足\(a_i\le a_j\&\&j=i+1\)。
然后这题就讲完了,但作为一道码农题,还是要注意以下细节。。
提示:因为线段树遍历是从左往右遍历,所以后一个遍历到的一定和前一个遍历到的相连,所以保存前一个序列的最后一位,直接比较即可(虽然我并没有用这一种办法
手起,码落,把这题咔嚓了:
#include<bits/stdc++.h>
#define re register
using namespace std;
inline int read()
{
re int x=0,f=1;
re char ch=getchar();
for(;ch>'9'||ch<'0';ch=getchar())if(ch=='-')f*=-1;
for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<1)+(x<<3)+(ch^48);
return x*f;
}
const int N=500005;
int n,m;
long long a[N],lazy[N<<2],ll[N<<2],rr[N<<2];
bool yor[N<<2];
void build(int l,int r,int x)
{
if(l==r){yor[x]=1,ll[x]=rr[x]=a[l];return ;}
re int mid=(l+r)>>1;
build(l,mid,x<<1),build(mid+1,r,x<<1|1);
ll[x]=ll[x<<1],rr[x]=rr[x<<1|1];
yor[x]=(yor[x<<1]&yor[x<<1|1]&(rr[x<<1]<=ll[x<<1|1]));
}
inline void Down(int x)
{
if(lazy[x])
{
ll[x<<1]+=lazy[x],rr[x<<1]+=lazy[x],ll[x<<1|1]+=lazy[x],rr[x<<1|1]+=lazy[x];
lazy[x<<1]+=lazy[x],lazy[x<<1|1]+=lazy[x];
lazy[x]=0;
}
}
void add(int l,int r,int x,int z,int L,int R)
{
if(L<=l&&r<=R){ll[x]+=z,rr[x]+=z,lazy[x]+=z;return ;}
Down(x);
re int mid=(l+r)>>1;
if(mid>=L)add(l,mid,x<<1,z,L,R);
if(mid<R)add(mid+1,r,x<<1|1,z,L,R);
ll[x]=ll[x<<1],rr[x]=rr[x<<1|1];
yor[x]=(yor[x<<1]&yor[x<<1|1]&(rr[x<<1]<=ll[x<<1|1]));
}
bool ask(int l,int r,int x,int L,int R)
{
if(L<=l&&r<=R)return yor[x];
Down(x);
re int mid=(l+r)>>1;
re bool ans=true;
if(mid>=L)ans&=ask(l,mid,x<<1,L,R);
if(mid<R)ans&=ask(mid+1,r,x<<1|1,L,R);
if(mid>=L&&mid<R)ans&=(rr[x<<1]<=ll[x<<1|1]);
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for(re int i=1;i<=n;i++)scanf("%lld",&a[i]);
build(1,n,1);
for(re int i=1,x,y;i<=m;i++)
{
if(read()==1)
{
x=read(),y=read();
add(1,n,1,read(),x,y);
}
else
{
x=read(),y=read();
ask(1,n,1,x,y)?puts("Yes"):puts("No");
}
}
return 0;
}
最水的一题,竟然放在T3。。
T4.Glass 玻璃
一句话题意:给出一棵树,每个点有点权,边有边权,求树上任意两点之间共\(n(n-1)\)条路径的边权和与点权和之积。\((n\le2\times10^6)\)
这题稍微有点意思,但也还是比较水的。
这题的方法是算每条边的贡献,即枚举每一条边,算出这条边对整个答案的贡献即可。
如下图
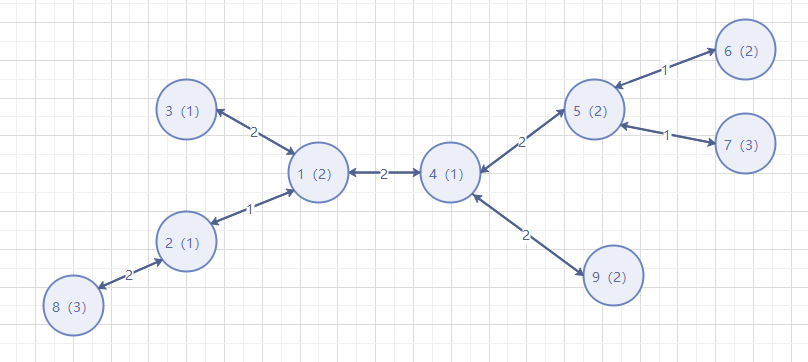
其中中间一条边权为\(2\)的边为我们枚举的边,而观察可以发现,每个点都要经过这条边和对面的点配对,其实我们可以只算一对,然后输出答案时乘以一个二就好了。
比如\(1\)号点(括号内为点权),要与右边每个点都匹配一次,而会发现\(4\)号点的点权要添加\(5\)次,其实添加的次数就是以它为根节点的子树的大小。我们就可以把它整个子树添加的权值加到根节点,然后每次枚举边只需要加上边两边的节点的权值和乘以这条边的权值就是这条边的贡献了,细节比较多,两遍DFS预处理,再一遍DFS枚举所有的边。
手起,码落,把这题咔嚓了:
#include<bits/stdc++.h>
#define re register
#define mod 998244353
using namespace std;
inline int read()
{
re int x=0,f=1;
re char ch=getchar();
for(;ch>'9'||ch<'0';ch=getchar())if(ch=='-')f*=-1;
for(;ch>='0'&&ch<='9';ch=getchar())x=(x<<1)+(x<<3)+(ch^48);
return x*f;
}
const int N=2000005;
struct edge{int v,net,val;}e[N<<1];
int n,a[N],cnt,hd[N];
long long ans,sum1[N],num[N],sum2[N];
inline void add(int val,int v,int u)
{
e[++cnt].v=v,e[cnt].net=hd[u],e[cnt].val=val,hd[u]=cnt;
e[++cnt].v=u,e[cnt].net=hd[v],e[cnt].val=val,hd[v]=cnt;
}
void dfs_first(int u,int fa)
{
num[u]=1;
for(re int i=hd[u],v;i;i=e[i].net)
{
v=e[i].v;
if(v==fa)continue;
dfs_first(v,u);
(num[u]+=num[v])%=mod;
(sum1[u]+=sum1[v])%=mod;
}
(sum1[u]+=num[u]*a[u]%mod)%=mod;
}
void dfs_second(int u,int fa)
{
for(re int i=hd[u],v;i;i=e[i].net)
{
v=e[i].v;
if(v==fa)continue;
(sum2[v]+=((sum2[u]-num[v]*a[u]%mod+mod)%mod+(num[1]-num[v])*a[v]%mod)%mod)%=mod;
dfs_second(v,u);
}
}
void getans(int u,int fa)
{
for(re int i=hd[u],v,mid;i;i=e[i].net)
{
v=e[i].v;
if(v==fa)continue;
(mid=((sum2[u]-num[v]*a[u]%mod+mod)%mod-sum1[v]+mod)%mod)%=mod;
(ans+=e[i].val*((mid*num[v]%mod+(sum2[v]-(num[1]-num[v])*a[v]%mod-mid+mod)%mod*(num[1]-num[v])%mod)%mod)%mod)%=mod;
getans(v,u);
}
}
int main()
{
scanf("%d",&n);
for(re int i=1;i<=n;i++)a[i]=read();
for(re int i=1;i<n;i++)add(read(),read(),read());
dfs_first(1,0);
sum2[1]=sum1[1],dfs_second(1,0);
getans(1,0);
printf("%lld",(ans<<1)%mod);
return 0;
}
除了这场比赛,还写了一道题,稍微讲一点吧。
P6042 「ACOI2020」学园祭
题目大意:定义:
\[\Gamma(0)=1,\Gamma(n)=n!
\]
\[A_i^j=\frac{\Gamma(i)}{\Gamma(j)}
\]
求:
\[\sum_{i=1}^n\sum_{j=1}^i\sum_{k=1}^j~\gcd(A_{i-j}^j\times\Gamma(j),A_{j-k}^k\times\Gamma(k))
\]
通过推一遍小学生都会的柿子,题目变成了求:
\[ans=\sum_{i=1}^n\sum_{j=1}^i\sum_{k=1}^j ~\min(i-j,j-k)~!
\]
然后?然后我就不会了。。还是借鉴借鉴题解吧:
因为\(k\le j\le i\le n\),所以\(\min(i-j,j-k)\le \lfloor\frac{n-1}{2}\rfloor\),所以柿子就可以变成\(ans=\sum_{a=0}^{\lfloor\frac{n-1}{2}\rfloor}a!\times num_a\),其中\(num_a\)为\(a!\)的出现次数。
我们设\(x=i-j,y=j-k\),然后我们假设\(x,y\)已知,就可以用含\(k\)的柿子表示\(i\)了:\(i=k+x+y\),又因为\(k\ge 1,i\le n\),所以\(1\le k\le n-x-y\)。而当\(k\)确定时,因为\(x,y\)确定,\(i,j\)也会被相应确定,所以总\(i,j,k\)共有\(n-x-y\)种取值。
然后接来算\(x,y\)有哪些情况了,因为\(\min(x,y)=a\),所以总共有两种情况:\(x=a,y\in \begin{bmatrix}a\sim n-a-1\end{bmatrix}\)和\(y=a,x\in \begin{bmatrix}a\sim n-a-1\end{bmatrix}\),还要注意的是,根据容斥,还要减去\(x=a,y=a\)的情况。
第一种情况根据\(i,j,k\)共有\(n-x-y\)种取值,推出方案数\(sum=\sum_{b=a}^{n-a-1}n-a-b\Rightarrow sum=\sum_{b=1}^{n-2a}b\Rightarrow sum=\frac{(n-2a+1)(n-2a)}{2}\)
第二种情况也是如此所以\(num_a=2\times \frac{(n-2a+1)(n-2a)}{2}-(n-2a)\Rightarrow num_a=(n-2a)^2\)
综上所述\(ans=\sum_{a=0}^{\lfloor\frac{n-1}{2}\rfloor}a!\times (n-2a)^2\Rightarrow ans=\sum_{a=0}^{\lfloor\frac{n-1}{2}\rfloor}a!\times n^2-a!\times4a+a!\times 4a^2\)
然后用前缀和维护\(a!,a!\times4a,a!\times4a\)就好了。
手起,码落,把这题咔嚓了:
#include<bits/stdc++.h>
#define re register
#define mod 10086001
using namespace std;
const int N=1000005;
int T;
long long sum1[N],sum2[N],sum3[N],jc,n,mid;
int main()
{
scanf("%d",&T);
sum1[0]=jc=1,sum2[0]=sum3[0]=0;
for(re long long i=1;i<=1000000;i++)
{
jc=(jc*i)%mod;
sum1[i]=(sum1[i-1]+jc)%mod;
sum2[i]=(sum2[i-1]+jc*(i<<2)%mod)%mod;
sum3[i]=(sum3[i-1]+jc*(i*i%mod<<2)%mod)%mod;
}
for(;T--;)
{
scanf("%lld",&n);
mid=(n-1)>>1;
printf("%lld\n",((sum1[mid]*n%mod*n%mod-sum2[mid]*n%mod+sum3[mid]+mod)%mod+mod)%mod);
}
return 0;
}

