[hdu5323]复杂度计算，dfs
题意：求最小的线段树的右端点（根节点表示区间[0,n]），使得给定的区间[L,R]是线段树的某个节点。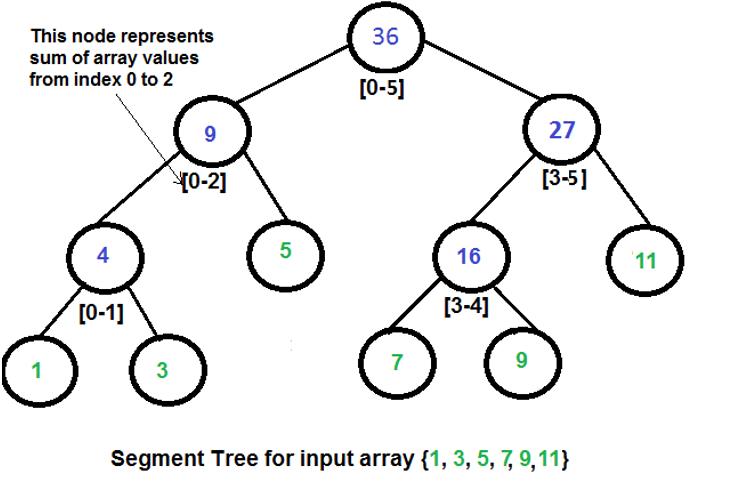
数据范围：L,R<=1e9,L/(R-L+1)<=2015
思路：首先从答案出发来判断是否出现给定区间是行不通的，于是只能从[L,R]出发来寻找答案。如果一个子节点表示区间[L,R]，那么它的父节点可能是四种表示方式之一，分别是[L,2R-L],[L,2R-L+1],[2L-R-1,R],[2L-R-2,R]，其中父节点为[L,2R-L]时要求R>L，否则它的右儿子就为空了，这是不允许的。接下来看无解的条件，如果L<(R-L+1)了，那么就是无解的，因为左儿子不可能比右儿子表示的区间长度小，也就是说L/(R-L+1)小于1时就可以判定为无解了。注意到由儿子节点到父亲节点，(R-L+1)变为了原来的两倍左右，而L是非增的，所以L/(R-L+1)每经过一层，值变为原来的1/2左右，有题目给定的数据，L/(R-L+1)<=2015，所以层数最多只有log22015=11，这不难想到dfs暴力扩展了，dfs总共只会扩展出4^11=4000000个节点，可以承受。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 | /* ******************************************************************************** */#include <iostream> //#include <cstdio> //#include <cmath> //#include <cstdlib> //#include <cstring> //#include <vector> //#include <ctime> //#include <deque> //#include <queue> //#include <algorithm> //using namespace std; // //#define pb push_back //#define mp make_pair //#define X first //#define Y second //#define all(a) (a).begin(), (a).end() //#define foreach(i, a) for (typeof(a.begin()) it = a.begin(); it != a.end(); it ++) // //void RI(vector<int>&a,int n){a.resize(n);for(int i=0;i<n;i++)scanf("%d",&a[i]);} //void RI(){}void RI(int&X){scanf("%d",&X);}template<typename...R> //void RI(int&f,R&...r){RI(f);RI(r...);}void RI(int*p,int*q){int d=p<q?1:-1; //while(p!=q){scanf("%d",p);p+=d;}}void print(){cout<<endl;}template<typename T> //void print(const T t){cout<<t<<endl;}template<typename F,typename...R> //void print(const F f,const R...r){cout<<f<<", ";print(r...);}template<typename T> //void print(T*p, T*q){int d=p<q?1:-1;while(p!=q){cout<<*p<<", ";p+=d;}cout<<endl;} // //typedef pair<int, int> pii; //typedef long long ll; //typedef unsigned long long ull; // ///* -------------------------------------------------------------------------------- */ //template<typename T>bool umax(T &a, const T &b) { return a >= b? false : (a = b, true);}ll ans, L, R;void dfs(ll L, ll R) { if (L == 0) { if (ans == -1 || ans > R) ans = R; return ; } ll s = L, t = R - L + 1; if (s < t) return ; if (L < R) dfs(L, 2 * R - L); dfs(L, 2 * R - L + 1); dfs(2 * L - R - 1, R); dfs(2 * L - R - 2, R);}int main() {#ifndef ONLINE_JUDGE freopen("in.txt", "r", stdin);#endif // ONLINE_JUDGE while (cin >> L >> R) { ans = -1; dfs(L, R); cout << ans << endl; } return 0; //} // // // ///* ******************************************************************************** */ |
