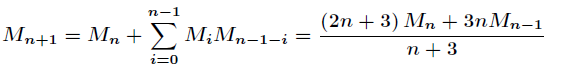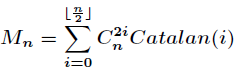转自 https://blog.csdn.net/ZCY19990813/article/details/81181505
一:环排列
把一个m个元素的环在m个不同的位置拆开记得到m个不同的线排列。由于n个不同元素中任取m个元素的排列方法为P(n,m)种,所以n个不同元素中任取m个元素的环排列方法有P(n,m)/m种。(p是排列组合中的A)
特别的,n个不同元素的环排列方法有P(n,n)/n=(n-1)!种。
二:母函数(用来解决:有N种重量的物品,每种物品有M个(1-无穷),求可以组合出来的重量的个数和该重量的方案数。)
#include<cstdio>
#include<iostream>
using namespace std;
const int MAXN = 300 + 10;
int a[MAXN];
int b[MAXN];
int main()
{
int n;
while(cin >> n && n)
{
for(int i = 0; i <= 300; i++) // 初始化
{
a[i] = 1; // 模拟第一个括号,各项的系数为1
b[i] = 0; // 中间数组
}
for(int i = 2; i <= 17; ++i) // 外层括号数
{
for(int j = 0; j <= n; ++j) // 因为没有限制硬币的数量,每步新形成的括号,
{
for(int k = 0; k + j <= n; k += i * i) 增量。
{
b[k + j] += a[j];
}
}
for(int j = 0; j <= n; ++j) // 因为
{
a[j] = b[j];
b[j] = 0;
}
}
cout << a[n] << endl;
}
return 0;
}
三:唯一分解定理
<1>容斥原理
容斥原理中经常用到的有如下两个公式:
1.两集合的容斥关系公式:A∪B=A+B-A∩B。
2.三个集合的容斥关系公式:A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C。
需要注意的是,以上两个公式分别主要针对两种情况:第一个公式是针对涉及到计算两类事物的个数,第二个公式是针对涉及到三类事物的个数。
<2>抽屉原理
桌上有十个苹果,要把这十个苹果放到九个抽屉里,无论怎样放,我们会发现至少会有一个抽屉里面至少放两个苹果。这一现象就是我们所说的“抽屉原理”。 抽屉原理的一般含义为:“如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有n+1个元素放到n个集合中去,其中必定有一个集合里至少有两个元素。” 抽屉原理有时也被称为鸽巢原理。它是组合数学中一个重要的原理。
四:卡特兰数
实际上就是出栈序列的种数,记得有一年蓝桥杯考的卡特兰数,当时还不知道,所以写了32个for循环
令h(0)=1,h(1)=1,catalan数满足递推式:
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)
例如:h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2
h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5
另类递推式:
h(n)=h(n-1)*(4*n-2)/(n+1);
递推关系的解为:
h(n)=C(2n,n)/(n+1) (n=0,1,2,...)
递推关系的另类解为:
h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,...)
相关题目链接:小兔的棋盘
http://acm.hdu.edu.cn/showproblem.php?pid=2067
#include<stdio.h>
int main()
{
__int64 a[36];
int i,j;
a[1]=1;
for(i=2; i<=35; i++)
a[i]=a[i-1]*1.0/(i+1)*(4*i-2);
int n;
int x=1;
while(scanf("%d",&n))
{
if(n==-1)
break;
printf("%d %d %I64d\n",x,n,2*a[n]);
x++;
}
return 0;
}
五:默慈金数 默慈金数是在数学中,一个给定的数n的默慈金数是“在一个圆上的n个点间,画出彼此不相交的弦的全部方法的总数”。
六 贝尔数
Bell数,又称为贝尔数。
B(n)是包含n个元素的集合的划分方法的数目。
B(0) = 1, B(1) = 1, B(2) = 2, B(3) = 5,
B(4) = 15, B(5) = 52, B(6) = 203,..
递推公式为,
B(0) = 1,
B(n+1) = Sum(0,n) C(n,k)B(k). n = 1,2,...
其中,Sum(0,n)表示对k从0到n求和,C(n,k) = n!/[k!(n-k)!]
七 那罗延数
N(n,k) = 1/n * C(n,k) * C(n,k-1)