7_6 带宽（UVa140）<回溯法：最优性剪枝>

给定一个图(V,E)，其中V为顶点的集合，E为边的集合，属于VxV。给定V中元素的一种排序，那么顶点v的带宽定义如下：在当前给定的排序中，与v距离最远的且与v有边相连的顶点与v的距离。给定排序的带宽定义为各顶点带宽的最大值。例如考虑如下图：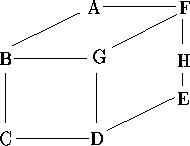

此图可以给出多种排序，其中两个排序图示如下：

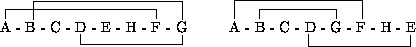
对于给出的这两个排序，它们各结点的带宽分别是（按排序顺序）：6, 6, 1, 4, 1, 1, 6, 6，排序带宽为6，以及5, 3, 1, 4, 3, 5, 1, 4，排序带宽为5。

写一个程序，找出该图的一种排序使其带宽最小。

Input
输入

输入由一系列的图构成。每个图独占一行。一个仅包含“#”字符的一行输入标志整个输入文件结束。对于每个图的输入，都包含一系列由“;”隔开的记录。每个记录包含一个结点名（一个大写字母，范围是“A”到“Z”），接着是一个“:”，然后是一些该结点的邻居结点。图中不会包含超过8个结点。

 

Output
输出

每个图对应一行输出，列出排序的结点，然后是一个箭头（->）以及该排序的带宽值。所有项都应由一个空格与它相邻的项隔开。如果同一个带宽有多种排序方法，取字母序最小的一种排序，也就是取字母表排在前面的一种排序。

Sample input

A:FB;B:GC;D:GC;F:AGH;E:HD
#

 

Sample output

 A B C F G D H E -> 3