彩色图像处理

彩色基础

什么是彩色
彩色是物体的一种属性，就像纹理、形状、重量一样． 通常， 它依赖于3个方面的因素：

• 光源一一照射光的谱性质或谱能量分布．
• 物体－一被照射物体的反射性质．
• 成像接收器（眼睛或成像传感器）一一光谱能量吸收性质

其中，光特性是颜色科学的核心。假如光没有颜色（捎色的，如观察者看到的黑白电视的光），那么它的属性仅仅是亮度或者数值。可以用灰度值来描述亮度， 光的范围从黑到灰．最后到白。
而对于彩色光，我们通常用3个基本量来描述其光源的质量： 辐射率、光强和亮度。
(1）辐射率是从光源流出能量的总量， 通常用瓦特(W）度量；
(2）光强用流明度量，它给出了观察者从光源接收的能量总和的度量：
(3）亮度是彩色强度概念的具体化。它实际上是一个难以度量的主关描绘子．
同样作为能量的度盘，辐射率与光强却往往没有必然的联系．例如，在进行X光检查时，光从X射线源中发出，它是具有实际意义上的能量的。但由于其处于可见光范围以外，观察者很难感觉到。因此对我们来说，它的光强几乎为o.

我们眼中的彩色
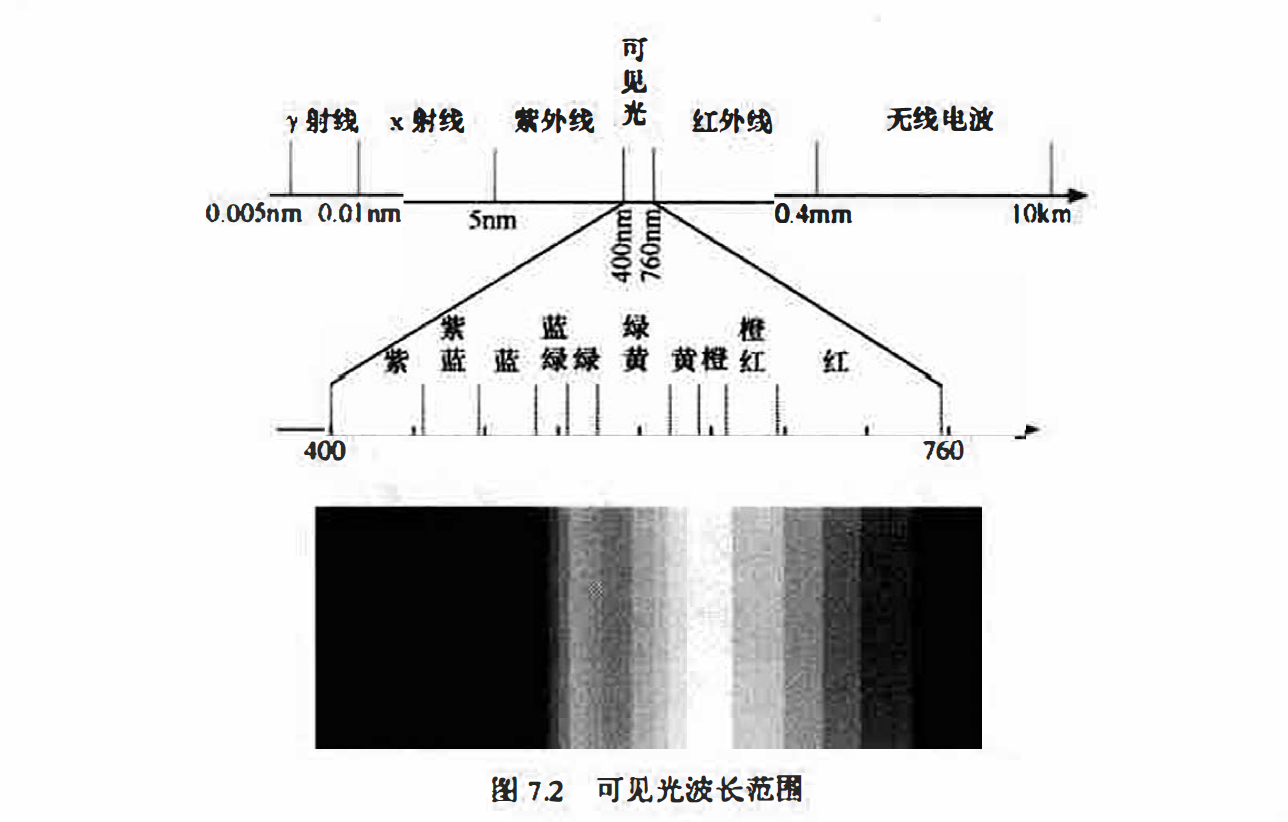
人类能够感受到的物体的颜色是由物体反射光的性质决定的，． 如图7.2所示，可见光是由电磁波谱中较窄的液段组成。如果物体反射的光在所有可见光披长范围内是平衡的， 则站在观察者的角度它就是白色的：如果物体仅对有限的可见光谱范围反射，则物体表现为某种特定颜色。例如，反射披长范围在450～500nm 之间的物体呈现蓝色， 它吸收了其他被长光的多数能量： 而如果物体吸收了所有的入射光，则将呈现为黑色。

三原色
据详细的实验结果可知，人眼中负责彩色感知的细胞中约有65%对红光敏感， 33%对绿光敏感，而只有2%对蓝光敏感。正是人眼的这些极收特性决定了被看到的彩色是通常所谓的原色红(R ）、绿(G ）、蓝(B）的各种组合。国际照明委员会（CIE ）规定以蓝=435.8nm、绿＝546.lnm、红＝700nm 作为主原色， 红CR ）、绿（G ）、蓝（ B ）也因此被称为3 原色。
在图7.3所示的CIE色度图中，最外围的轮廓对应所有的可见光谱色，在其边缘上标出了对应的波长值（以m为单位〉，该轮廓之内的区域包含了所有的可见颜色．如果将色度圈中的三色点两两连接成一个三角形， 则该三角形内的任何颜色都可以自这3种原色的不同混合产生。

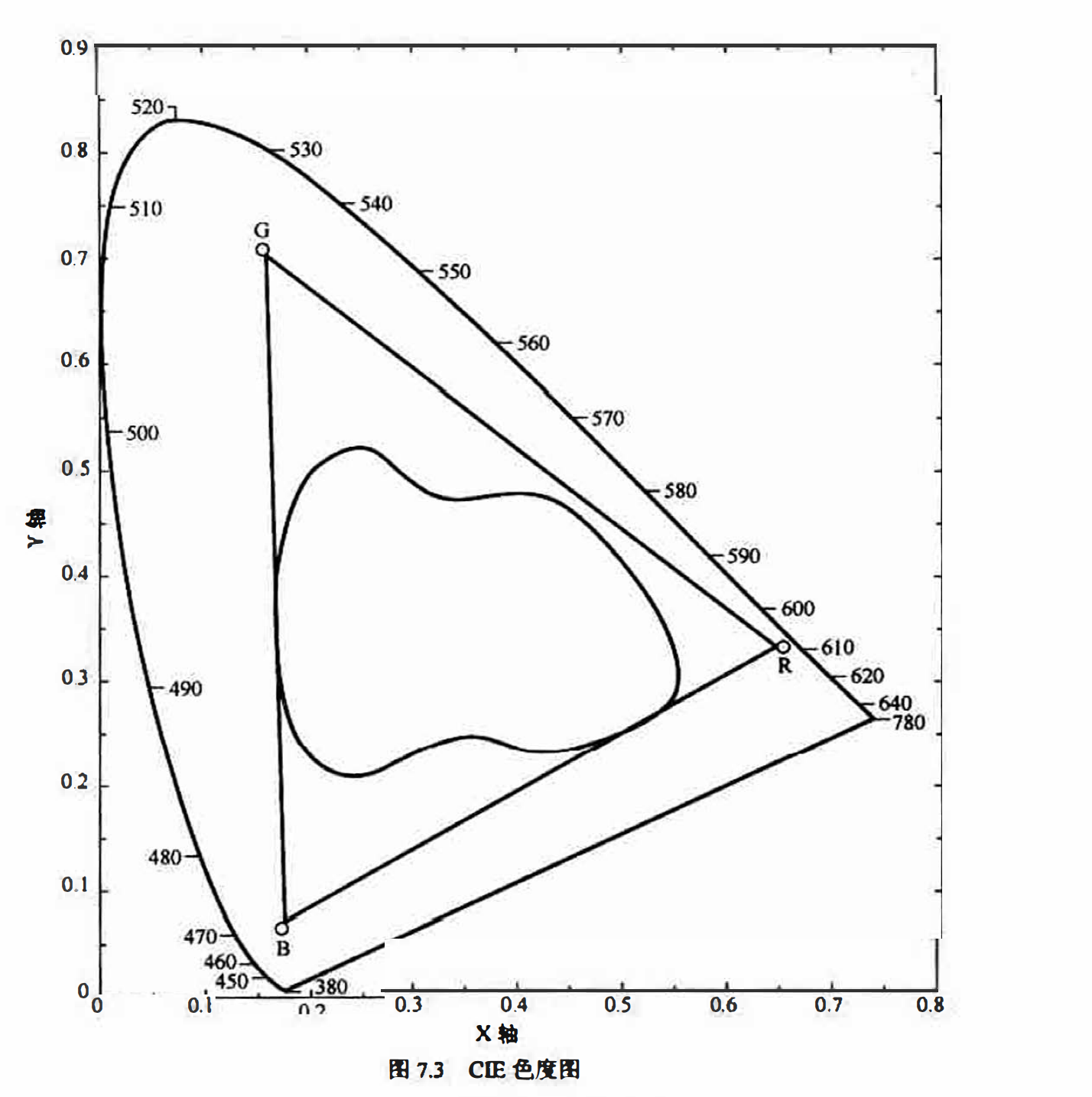
我们看到， 图7.3中由R、G、B三种标准原色所连成的三角形并不能涵盖整个可见颜色区域， 这说明仅使用三原色并不能得到所有的可见颜色。事实上， 图7.3中的三角形区域对应着典型的RGB监视器所能够产生的颜色范围， 称为彩色全域：而在三角形内不规则的区域表示高质量的彩色打印设备的彩色域．

计算机中的颜色表示
在计算机中，显示器的任何颜色〈色彩全域〉都可以自红、绿、蓝3种颜色组成，称为三基色．每种基色的取值范围是0～255.任何颜色都可以用这3种颜色按不同的比例混合而成， 这就是三原色原理． 在计算机中， 三原色的原理可以这样解释:

• 计算机中的任何颜色都可以由3种颜色按不同比例混合而成；而每种颜色也都可以分解成三种基本颜色．
• 三原色之间相互独立，任何一种颜色都不能由其余两种颜色组成．
• 混合色的饱和度由3种颜色的比例来决定 混合色的亮度为3种颜色的亮度之和．
  

彩色模型

彩色模型也称彩色空间或彩色系统， 是用来精确标定和生成各种颜色的一套规则和定义， 它的用途是在某些标准下用通常可接受的方式简化彩色规范． 彩色模型通常可以采用坐标系统来描述， 而位于系统中的每种颜色都由坐标空间中的单个点来表示。
如今使用的大部分彩色模型都是面向应用或是面向硬件， 比如众所周知的针对彩色电视器的RGB（ 红、绿、蓝〉模型， 以及面向彩色打印机的CMY（青、深红、黄〉和CMYK(青、深红、黄、黑〉模型。而HSI(色调、饱和度、亮度〉模型非常符合人眼描述和解释颜色的
方式。此外， 目前广泛使用的彩色模型还有如：HSV模型、YUV 模型、YIQ模型、Lab模型等。下面将分别介绍这些彩色模型并给出它们与最为常用的RGB模型之间的转换方式。

RGB模型

RGB模型是工业界的一种颜色标准． 是通过对红（Red）、绿（Green）、蓝(Blue)3种颜色亮度的变化以及它们相互之间的叠加来得到各种各样的颜色的。该标准儿乎包括了人类视觉所能感知的所有颜色，是目前运用最广的颜色模型之一。
理论基础
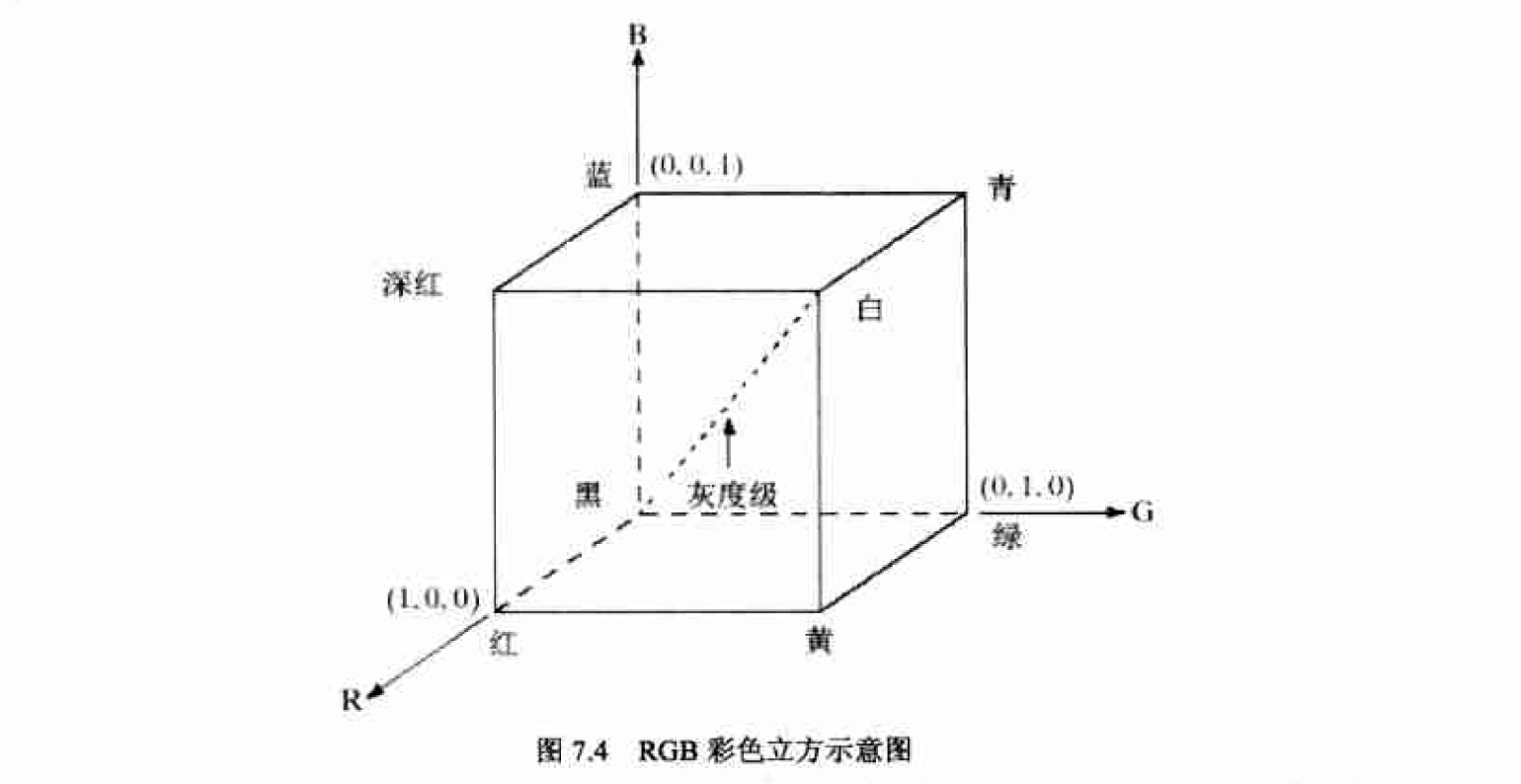
RGB彩色空间对应的坐标系统是如图7.4所示的立方体． 红、绿和蓝位手立方体的3个顶点上：青、深红和黄位于另外3个顶点上：黑色在原点处， 而白色位于距离原点最远的顶点处， 灰度等级就沿这两点连线分布： 不同的颜色处于立方体外部和内部， 因此可以用一个3维向量来表示。例如，在所有颜色均己归一化到（O, 1）的情况下，蓝色可表示为（O, 0, 1),而灰色可由向量（0.5, 0.5, 0.5）来表示。
在RGB模型中，3个图像分量组成了所要表示的图像，而每一个分量图像都是其原色图像，如图7.5所示。当送入RGB监视器时，这3个分量图像便在屏上混合产生一幅合成彩色图像：　

在RGB空间中，用以表示每一像素的比特数叫做像素深度。RGB图像的3个红、绿、 蓝分量图像都是一幅8比特图像，每一个彩色像素有24比特深度。因此，全彩色图像常用来定义24比特的彩色图像，颜色总数是(28)3=16777216

matlab实现

CMY、CMYK模型

CMY模型（Cyan、Magenta、Yellow）是采用青、品红、黄色3种基本原色按一定比例合成颜色的方法。由于色彩的显示不是直接来自于光线的色彩，而是由光线被物体吸收掉一部分之后反射回来的剩余光线产生，因此CMY模型又称为减色法混色模型。当光线都被吸收时成为黑色，都被反射时成为白色．

像CMY 模型这样的减色混合模型正好适用于彩色打印机和复印机这类需要在纸上沉积彩色颜料的设备， 因为颜料不是像显示器那样发出颜色， 而是反射颜色。例如，当青色颜料涂覆的表面用。白光照射时， 从该表面反射的不是红光， 而是从反射的白光中减去红色得到的青色（白光本身是等量的红、绿、蓝光的组合）. CMY模型的颜料混合效果如图7.6所示， 注意这里的混合是原色的相减， 与
RGB模型的混合正好相反。

CMYK模型
由图7.6可见， 等量的颜料原色（青、品红和黄）可以混合产生黑色。然而在实际运用
中， 通过这些颜色混合产生的黑色是不纯的。因此， 为产生真正的黑色〈黑色在打印中起主
要作用〉， 专门在CMY模型中加入了第4种颜色一一黑色， 从而得到CMYK影色模型． 这
样当出版商说到“ 四色打印” 时， 即指CMY彩色模型的3种原色再加上黑色。

HSI模型

HSI模型是从人的视觉系统出发，直接使用颜色三要素色调（Hue）、饱和度（Saturation) 和亮度(intensity，有时也翻译作密度或灰度〉来描述颜色.

• 亮度是指人眼感觉光的明暗程度．光的能量越大，亮度越大．
• 色调是彩色最重要的属性，决定颜色的本质，由物体反射光线中占优势的波长来决定． 不同的波长产生不同的颜色感觉，我们叫来一种颜色为红、橙、黄，这就是说我们在规定一种色调．
• 饱和度是指颜色的深浅和浓淡程度，饱和度越高，颜色越深．饱和度的深浅和白色的 比例有关，白色所占比例越高，饱和度越低．

HSI彩色空间可以用一个圆锥空间模型来描述， 如图7.8所示。我们通常把色调和饱和度统称为色度， 用来表示颜色的类别与深浅程度。在图中
四锥中间的横截面圆就是色度圆， 而圆锥向上或向下延伸的便是亮度分量的表示．
由于人的视觉对亮度的敏感程度远强于对颜色浓淡的敏感程度， 为了便于颜色处理和识别， 人的视觉系统经常采用HSI彩色空间， 它比RGB彩色空间更符合人的视觉特性。此外， 由于HSl空间中亮度和色度具有可分离特性， 使得图像处理和机器视觉中大量灰度处理算法都可在
HSI彩色空间中方便地使用。
HSI彩色空间和RGB 彩色空间只是同一物理量的不同表示法， 它们之间存在着转换关系． 下面将介绍RGB到到HSI的彩色转换和HSI到RGB的彩色转换

从RGB到HSI的彩色转换及其实现
给定一幅RGB格式的图像， 每一个RGB像素和H分量可用下面的公式得到：

matlab实现

function hsi = rgb2hsi(rgb)
% hsi = rgb2hsi(rgb)把一幅RGB图像转换为HSI图像，
% 输入图像是一个彩色像素的M×N×3的数组，
% 其中每一个彩色像素都在特定空间位置的彩色图像中对应红、绿、蓝三个分量。
% 假如所有的RGB分量是均衡的，那么HSI转换就是未定义的。
% 输入图像可能是double（取值范围是[0, 1]），uint8或 uint16。
%
% 输出HSI图像是double，
% 其中hsi(:, :, 1)是色度分量，它的范围是除以2*pi后的[0, 1]；
% hsi(:, :, 2)是饱和度分量，范围是[0, 1]；
% hsi(:, :, 3)是亮度分量，范围是[0, 1]。

% 抽取图像分量
rgb = im2double(rgb);
r = rgb(:, :, 1);
g = rgb(:, :, 2);
b = rgb(:, :, 3);

% 执行转换方程
num = 0.5*((r - g) + (r - b));
den = sqrt((r - g).^2 + (r - b).*(g - b));
theta = acos(num./(den + eps)); %防止除数为0

H = theta;
H(b > g) = 2*pi - H(b > g);
H = H/(2*pi);

num = min(min(r, g), b);
den = r + g + b;
den(den == 0) = eps; %防止除数为0
S = 1 - 3.* num./den;

H(S == 0) = 0;

I = (r + g + b)/3;

% 将3个分量联合成为一个HSI图像
hsi = cat(3, H, S, I);

从HSI到RGB的彩色转换及其实现
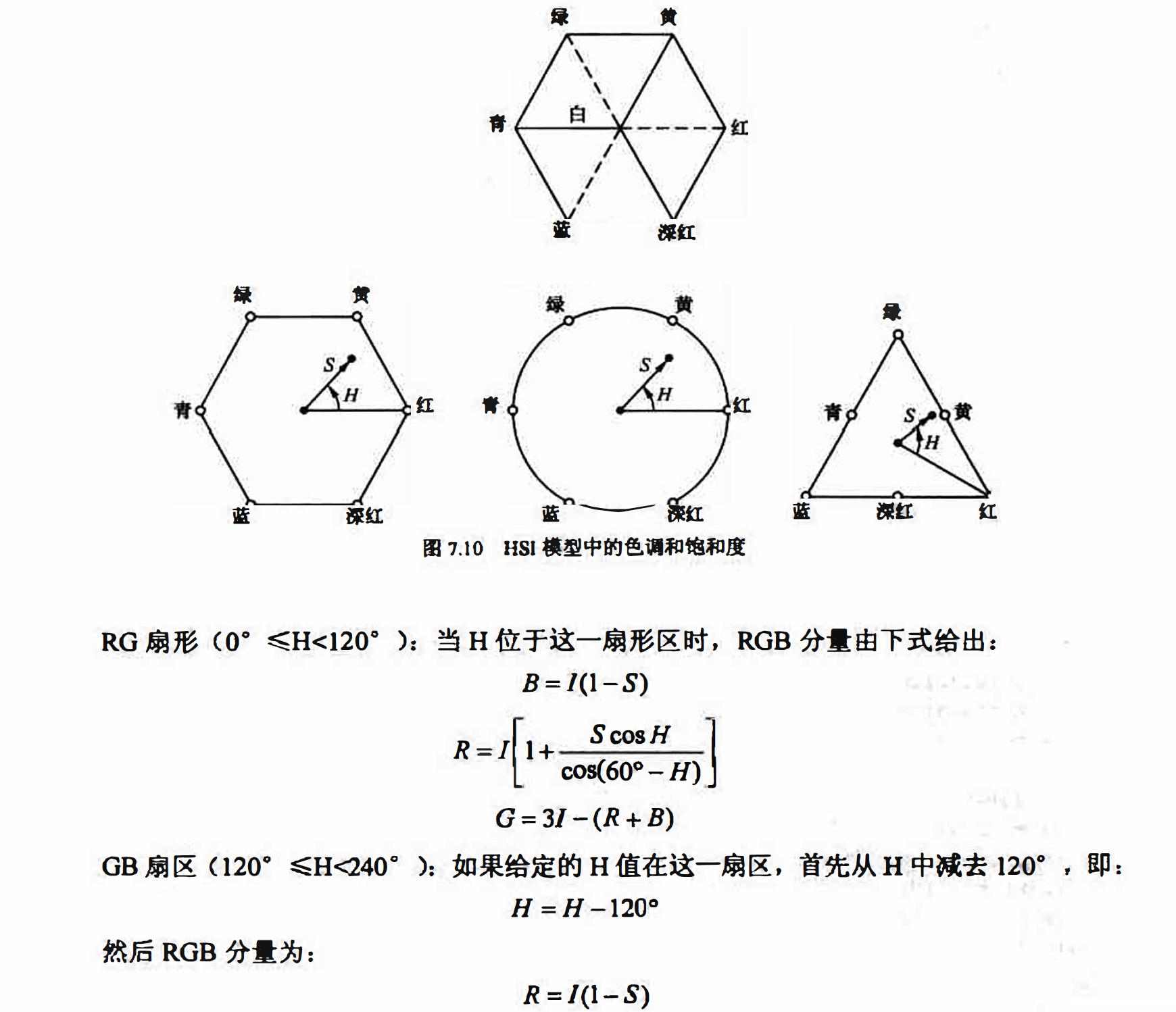
在［O, 1]内给出HSI值， 现在要在相同的值域找到RGB值， 可利用H值公式。在原始色分割中有3个相隔120· 的扇形， 如图7.10所示。从H乘以360＂ 开始， 这时色调值返回原来的[0,360]的范围．

matlab实现

function rgb = hsi2rgb(hsi)
% rgb = hsi2rgb(hsi)把一幅HSI图像转换为RGB图像，
% 其中hsi(:, :, 1)是色度分量，它的范围是除以2*pi后的[0, 1]；
% hsi(:, :, 2)是饱和度分量，范围是[0, 1]；
% hsi(:, :, 3)是亮度分量，范围是[0, 1]。
%
% 输出图像分量：
% rgb(:, :, 1)为红；
% rgb(:, :, 2)为绿；
% rgb(:, :, 3)为蓝。

% 抽取图像分量
hsi = im2double(hsi);
H = hsi(:, :, 1) * 2 * pi;
S = hsi(:, :, 2);
I = hsi(:, :, 3);

% 执行转换方程
R = zeros(size(hsi, 1), size(hsi, 2));
G = zeros(size(hsi, 1), size(hsi, 2));
B = zeros(size(hsi, 1), size(hsi, 2));

% RG扇形(0 <= H < 2*pi/3)
idx = find( (0 <= H) & (H < 2*pi/3));
B(idx) = I(idx) .* (1 - S(idx));
R(idx) = I(idx) .* (1 + S(idx) .* cos(H(idx)) ./ ...
cos(pi/3 - H(idx)));
G(idx) = 3*I(idx) - (R(idx) + B(idx));

% BG扇形(2*pi/3 <= H < 4*pi/3)
idx = find( (2*pi/3 <= H) & (H < 4*pi/3) );
R(idx) = I(idx) .* (1 - S(idx));
G(idx) = I(idx) .* (1 + S(idx) .* cos(H(idx) - 2*pi/3) ./ ...
cos(pi - H(idx)));
B(idx) = 3*I(idx) - (R(idx) + G(idx));

% BR扇形
idx = find( (4*pi/3 <= H) & (H <= 2*pi));
G(idx) = I(idx) .* (1 - S(idx));
B(idx) = I(idx) .* (1 + S(idx) .* cos(H(idx) - 4*pi/3) ./ ...
cos(5*pi/3 - H(idx)));
R(idx) = 3*I(idx) - (G(idx) + B(idx));

% 将3个分量联合成为一个RGB图像
rgb = cat(3, R, G, B);
rgb = max(min(rgb, 1), 0);

全彩色图像处理基础

本节主要介绍全彩色图像处理技术，以及面对不同的图像处理任务怎样处理全彩色图像．通常，全彩色图像处理技术总的可以分为以下两大类。
(1）对3个平面分量单独处理，然后将分别处理过的3个分量合成彩色图像。对每个分量的处理技术可以应用到对灰度图像处理的技术上。但是这种通道式的独立处理技术忽略了通道间的相互影响。
(2）直接对彩色像素进行处理。因为全彩色图像至少有3个分量，彩色像素实际上是一个向量。直接处理就是同时对所有分量进行无差别的处理．这时彩色图像的 3个分量用向量形式表示，即对彩色图像上任一点的像素 c(x,y)，有：
c(x,y)= [R(x,y);G(x,y);B(x,y)]
那么对像素点(x,y）处理的操作实际上是同时对 R、G、 B这3个分量操作．不过通常大多数图像处理技术都是指对每个分量的单独处理。接下来将讲述全彩色图像处理的两个常用技术：彩色补偿和彩色平衡。

彩色补偿及其Matlab实现

有些图像处理任务的目标是根据颜色分离出不同类型的物体。但由于常用的彩色成像设备具有较宽且相互覆盖的光谱敏感区，加之待拍摄图像的染色是变化的，所以很难在3 个分量图中将物体分离出来，这种现象称为颜色扩散。彩色补偿的作用就是通过不同的颜色通道提取不同的目标物。

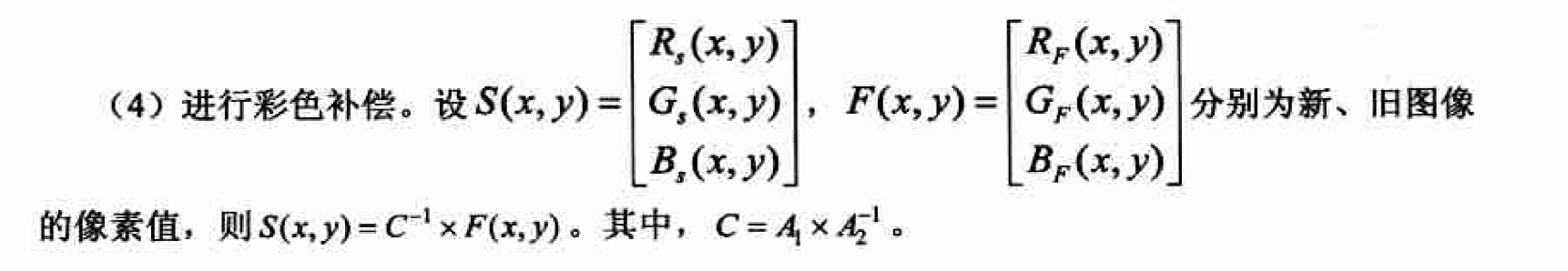
matlab实现

% compensate.m
% 彩色补偿
im=double(imread('plane.bmp'));
subplot(1,2,1);
imshow(uint8(im));
title('原始图');
[m,n,p]=size(im);
[h1,k1]=min(255-im(:,:,1)+im(:,:,2)+im(:,:,3));
[j1,minx]=min(h1);
 i1=k1(j1);%提取图像中最接近红色的点，其在im中的坐标为i1,j1
 r1=im(i1,j1,1);
 g1=im(i1,j1,2);
 b1=im(i1,j1,3);
R=0.30*r1+0.59*g1+0.11*b1;

[h2,k2]=min(255-im(:,:,2)+im(:,:,1)+im(:,:,3));
[j2,minx]=min(h2);
 i2=k2(j2);%提取图像中最接近绿色的点，其在im中的坐标为i2,j2
 r2=im(i2,j2,1);
 g2=im(i2,j2,2);
 b2=im(i2,j2,3);
G=0.30*r2+0.59*g2+0.11*b2;

[h3,k3]=min(255-im(:,:,3)+im(:,:,1)+im(:,:,2));
[j3,minx]=min(h3);
 i3=k3(j3);%提取图像中最接近蓝色的点，其在im中的坐标为i3,j3
 r3=im(i3,j3,1);
 g3=im(i3,j3,2);
 b3=im(i3,j3,3);
B=0.30*r3+0.59*g3+0.11*b3;

A1=[r1 r2 r3
    g1 g2 g3
    b1 b2 b3];
A2=[R 0 0
    0 G 0
    0 0 B];
C=A1*inv(A2);

for i=1:m
    for j=1:n

          imR=im(i,j,1);
          imG=im(i,j,2);
          imB=im(i,j,3);
          temp=inv(C)*[imR;imG;imB];
          S(i,j,1)=temp(1);
          S(i,j,2)=temp(2);
          S(i,j,3)=temp(3);
    end
end
S=uint8(S);
subplot(1,2,2);
imshow(S);
title('补偿后');

彩色平衡及其Matlab实现

一幅彩色图像数字化后， 在显示时颜色经常看起来有些不正常。 这是色通道的不同敏感度、增光因子和偏移量等原因导致的，称其为三基色不平衡。将之校正的过程就是彩色平衡

matlab实现

% balance.m
% 彩色平衡

im=double(imread('plane.bmp'));
[m,n,p]=size(im);
F1=im(1,1,:);
F2=im(1,2,:);
F1_(1,1,1)=F1(:,:,2);
F1_(1,1,2)=F1(:,:,2);
F1_(1,1,3)=F1(:,:,2);
F2_(1,1,1)=F2(:,:,2);
F2_(1,1,2)=F2(:,:,2);
F2_(1,1,3)=F2(:,:,2);
K1=(F1_(1,1,1)-F2_(1,1,1))/(F1(1,1,1)-F2(1,1,1));
K2=F1_(1,1,1)-K1*F1(1,1,1);
L1=(F1_(1,1,3)-F2_(1,1,3))/(F1(1,1,3)-F2(1,1,3));
L2=F1_(1,1,3)-L1*F1(1,1,3);
for i=1:m
    for j=1:n
          new(i,j,1)=K1*im(i,j,1)+K2;
          new(i,j,2)=im(i,j,2);
          new(i,j,3)=L1*im(i,j,3)+L2;
    end
end
im=uint8(im);
new=uint8(new);
subplot(1,2,1);
imshow(im);
title('原始图');
subplot(1,2,2);
imshow(new);
title('平衡后');