数字图像处理入门

图像是指能在人的视觉系统中产生视觉印象的客观对象，包括自然景物、拍摄到的图片、用数学方法描述的图形.图像的要素有儿何要素〈刻画对象的轮廓、 形状等〉和非几何要素（刻画对象的颜色、 材质等〉。

什么是数字图像
简单地说， 数字图像就是能够在计算机上显示和处理的图像， 根据其特性可分为两大类一一位图和矢量圈。 位图通常使用数字阵列来表示， 常见格式有BMP、 1町、 GlF等：矢量图由矢量数据库表示， 我们接触最多的就是PNG图形。

我们可以将一幅图像视为一个二维函数f(x，y)外， 其中x和y是空间坐标， 而在x-y 平面
中的任意一对空间坐标（x,y ） 上的幅值f称为该点图像的灰度、亮度或强度。此时， 如果f，
X, y均为非负有限离散， 则称该图像为数字图像〈位图〉。

一个大小为M×N的数字图像是由M行N列的有限元素组成的， 每个元素都有特定的
位置和幅值， 代表了其所在行列位置上的图像物理信息， 如灰度和色彩等。这些元素称为图
像元素或像素．

坐标约定
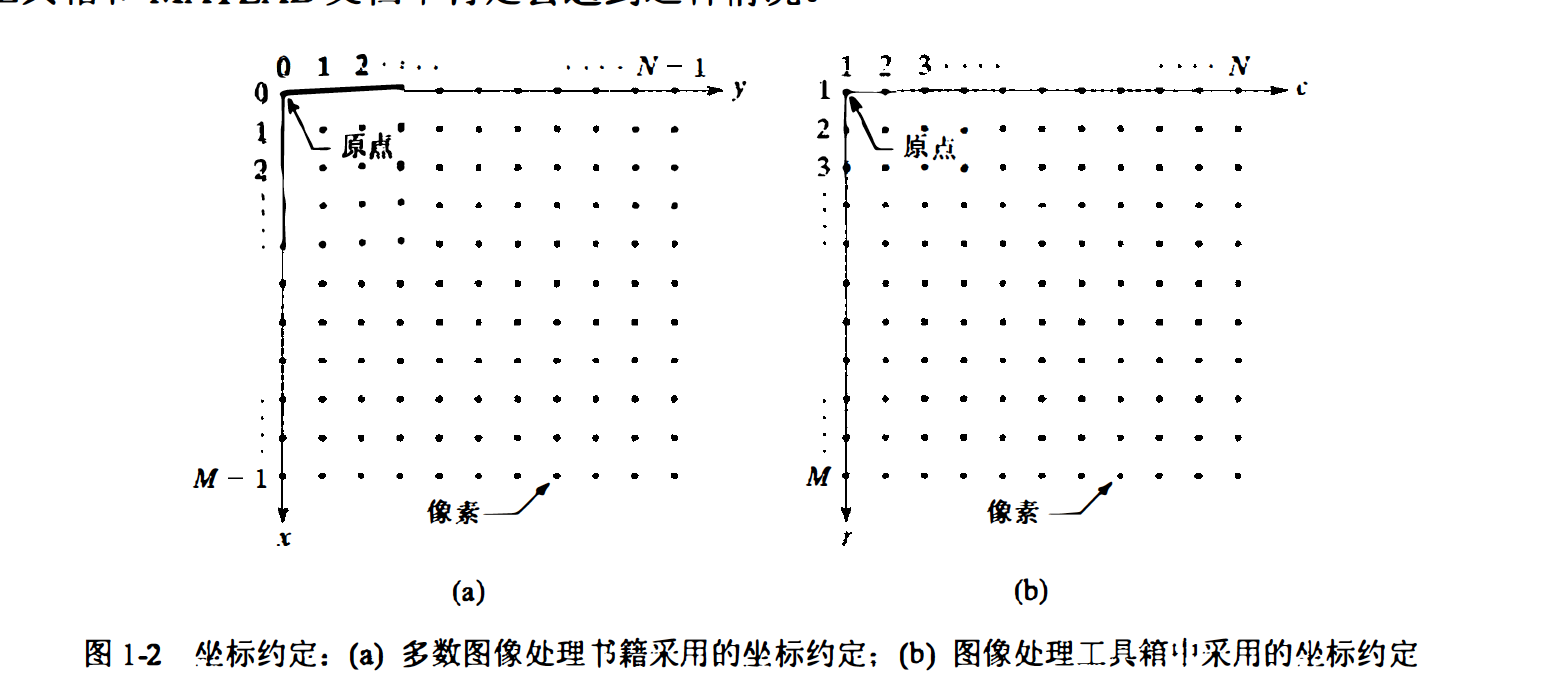
取样和量化的结果是实数矩阵。 本书采用两种主要方法来表示数字图像。 假设对一幅图像 f(x,y）进行采样后，可得到一幅M行、 N 列的图像，我们称这幅图像的大小是M×N。 相应的 值是离散的。 为使符号清晰和方便起见，这些离散的些标都取整数。 在很多图像处理书籍中， 图像的原点被定义为（x,y)=(O，0)的。图像中沿着第 1 行的下一坐标点为(x, y)=(O,1）。 符号（0,1）用来表示沿着第 1 行的第 2 个取样。当图像被取样时，并不意味着在物理坐标中存在实际值。图 1-2（时 显示了这一坐标约定。 注意x是从 0 到 M一I 的整数，y是从 0 到 N-I 的整数。

图像处理工具箱中表示数组使用的坐标约定与前面描述的坐标约定有两处不同。 首先，工 具箱用（r,c） 而不是（x,y）来表示行与列。然而，坐标顺序与前面讨论的是一样的。 在这种情况下， 坐标对（a,b）的第 1 个元素表示行，第 2 个元素表示列。其次，这个坐标系统的原点在（r,c)=(l,1) 处。 因此，r 是从 1 到M的整数，c 是从 1 到N的整数。 图 1-2(b）说明了这一坐标约定。
图像处理工具箱文档引用图 1-2(b）中的坐标作为像素坐标。

其中， 行列 （M行N列〉 必须为正整数， 离散灰度级数目L 一般为2的k次幂,k 为整数〈因为使用二进制整数值表示灰度值〉， 图像的动态范围为［O, L-1］， 那么图像存储所需的比特数为 b = M×N×k。 需要注意的是在矩阵f(y,x）中， 一般采用先行下标、 后列下标的表示方法， 因此这里先是纵坐标y（对应行〉， 然后才是横坐标 x（对应列〉。

而有些图像矩阵中， 很多像素的值都是相同的． 例如一个在纯黑背景上使用不同灰度勾勒的图像， 其多数像素的值都会是0。 这种矩阵称为稀疏矩阵（Sparse地面川， 可以通过简单描述非零元素的值和位置来代替大量地写入0元素。 这时存储图像需要的比特数可能大大减少。

图像的矩阵表示

图像的输入输出和显示
可以使用函数imread将图像读入MATLAB环境，imread的基本语法是：
imread （’filename’｝
此处，filename是含有图像文件全名的字符串（包括任何可用的扩展名）。例如语句

f = imread('Fig0101.tif');

将图像fig0101读取到图像数组f中。注意，单引号（’）是用来界定filename文件名字符串的，而命令行结尾处的分号在MATLAB中用于禁止输出。假如命令行中未包括分号，MATLAB将显示这一命令行指定的运算结果。当在MATLAB命令行窗口中出现提示符（》）时，表明命令行的开始

使用imshow函数在MATLAB桌面显示图像，imshow的基本语法是：imshow(f)
其中f是图像数组

图1-1显示了在屏幕上的输出。注意，图窗编号出现在最终得到的图窗的左上部。如果另一
幅图像q随后用imshow来显示，MATLAB就用新图像取代

》figure,imshow(g) 
使用imwrite函数将图像写入当前日录，imwrite的基本语法如下：   
imwrite(f，’filename') 

类和图像类型
虽然使用的是整数坐标， 但 MATLAB 中的像素值（亮度）并未限制为整数。 表 1-1 列出了 MATLAB 和图像处理工具箱为描述像素值而支持的各种类。 表中的前 8 项是数值型的数据类，第 9 项称为字符类， 最后一项称为逻辑类。
uint8 和 logical 类广泛用于图像处理， 当以 TIFF 或 JPEG 图像文件格式读取图像时，会用到这两个类。 这两个类用1个字节表示每个像素。某些科研数据源， 比如医学成像， 要求提供超出 uint8 的动态范围：针对此类数据， 会采用 uint16 和 int16 类。 这两个类为每个矩阵元素使用2 个字节。针对计算灰度的操作， 比如傅立叶变换（见第 3 章）， 使用 double 和single 浮点类。 双精度浮点数每个数组元素使用8 个宇节， 而单精度浮点数使用 4 个字节。尽管工具箱支持 int8 、 uint32 和 int32 类， 但在图像处理中并不常用

工具箱支持4种图像类型

• 灰度图像
• 二值图像
• 索引图像
• rgb图像

1.二值图像
每个像素只有黑、 自两种颜色的图像称为二值图像。 在二值图像中，像素只有 0和1两种取值， 一般用0来表示黑色， 用1表示白色．

2.灰度图像
在二值图像中进一步·加入许多介于黑色与白色之间的颜色探度，就构成了灰度图像。这类图像通常显示为从最暗黑色到最亮的白色的灰度，每种灰度〈颜色深度〉称为一个灰度级， 通常用L表示.在灰度图像中，像素可以取 O～L-1之间的整数值， 根据保存灰度数值所使用的数据类型的不同， 可能有256种取值或者 2k种取值， 当k=1时即退化为二值图像．

3.RGB图像
众所周知， 自然界中几乎所有颜色都可以自红（Red,R）、 绿（Green,G）、蓝（Blue,B) 3种颜色组合而戚，通常称它们为RGB三原色． 计算机显示彩色图像时采用最多的就是RGB模型。 对于每个像素，通过控制R、G、B三原色的合成比例则可决定该像素的 最终显示颜色．

对于三原色RGB中的每一种颜色． 可以像灰度图那样使用L个等级来表示含有这种颜
色成份的多少。 例如对于含有256个等级的红色， 0表示不含红色成份， 255表示含有10仍也
的红色成份． 同样， 绿色和蓝色也可以划分为256个等级。 这样每种原色可以用8位二进制
数据表示，于是3原色总共需要24位二进制数，这样能够表示出的颜色种类数目为256× 256×256==224，大约有1600万种， 己经远远超过普通人所能分辨出的颜色数目．
RGB颜色代码可以使用十六进制数以减少书写长度， 按照两位一组的方式依次书写R、 G、B三种颜色的级别.

未经压缩的原始BMP文件就是使用RGB标准给出的3个数值来存储图像数据的，称为
RGB图像。在RGB图像中每个像素都是用24位二进制数表示，故也称为24位真彩色图像。

4.索引图像
如果对每个像素都直接使用24 位二进制数表示， 图像文件的体积将变得十分庞大。举个
伊序． 对一个长、宽各为200像素， 颜色数为16的彩色图像， 每个像素都用RGB3个分量表
示，这样每个像素由3个字节表示，整个图像就是200×200×3=120园。这种完全未经压缩的
表示方式， 浪费了大量的存储空间， 下面简单介绍另一种更节省空间的存储方式:索引图像.

同样还是200像素×200像素的16色图像． 由于这张图片中最多只有16种颜色， 那么
可以用一张颜色表（16×3的二维数组〉保存这16种颜色对应的RGB值， 在表示图像的矩
阵中使用这16种颜色在颜色表中的索引〈偏移量〉作为数据写入相应的行列位置。例如，颜
色表中第3个元素为0XAA1111， 那么在图像中所有颜色为0XAA1111 的像索均可以由3-1=2
表示〈颜色表索引下标从0开始〉． 如此，每一个像素需要使用的二进制数就仅仅为4位（0.5
字节〉，整个图像只需要200×200× 0.5=20kB就可以存储， 而不会影响显示质量。

上文所指的颜色表就是常说的调色板（Palete），另一种说法叫做颜色查找表（LUT, Look
Up Table）。Wmdows位图中就应用调色板技术．其实不仅是Windows位图，许多其他的图像
文件格式比如PCX, TIF, GJF都应用了这种技术。

在实际应用中， 调色板中通常不足256种颜色． 在使用许多图像编辑工具生成图像或者
编辑GIF文件时，系统常常会提示用户选择文件包含的颜色数目。当选择较低的颜色数目时，
会有效地降低图像文件的体积， 在一定程度上也会降低图像的质量。
使用调色板技术喊小图像文件体积的条件是图像的像素数目相对较多，而颜色种类相对
较少．如果一个图像中用到了全部的24位真彩色，则对其使用颜色查找表技术完全没有意义，单纯从颜色角度对其进行压缩是不可能的。

数字图像的实质
f(x,y)的定义只适用于最一般的情况，即静态的灰度图像，严格来说，数字图像可以是2个变量（对于静止图像）或者3个变量（对于动态画面）
的离散函数。在静态图像的情况下是f(x,y)，但在动态画面下，则还需要时间参数t，即f(x, y, t）：函数值可能是个数值（对于灰度图像〉，也可能是个
向量（对于彩色图像)

图像的空间和灰度级分辨率

图像的空间分辩率（Spatial Resolution〉
图像的空间分辨率是指图像中每单位长度所包含的像素或点的数目，常以像素／英寸( pixels per inch,ppi)。为单位来表示。 如72ppi表示图像中每英寸包含72个像素或点． 分辨率越高， 图像越清晰， 图像文件所需的磁盘空间也越大， 编辑和处理所需的时间也越长。

像素越小， 单位长度所包含的像素数据就越多， 分辨率也就越高， 但同样物理大小范围内所对应图像的尺寸也会越大， 存储图像所需要的字节数也越多。 因而， 在图像的放大缩小算法中，放大是对图像的过采样，缩小则是对图像的欠采样，这些内容会在“4.5节图像缩放” 中进一步介绍．

通常在没有必要对涉及像素的物理分辨率进行实际度量时， 通常会称一幅大小为 M×N的数字图像的空间分辨率为M×N像素。

图0.3给出了同一幅图像在不同的空间分辨率下呈现出的不同效果． 当高分辨率下的图像以低分辨率表示时， 在同等的显示或打印输出条件下， 图像的尺寸会变小， 细节变得不明显： 当将低分辨率下的图像放大时， 则会导致图像的细节仍然模糊， 只是尺寸变大。 这是因为缩小的图像已经丢失了大量的信息， 在放大图像时只能通过复制行列的插值方法来确定新增像素的取值。

图像的灰度级／辐射计量分辩率
在数字图像处理中，灰度级分辨率又称色阶，是指图像中可分辨的灰度级数目，即前文提到的灰度级数目L，它与存储灰度级别所使用的数据类型有关。由于灰度级度量的是投射 到传感器上光辐射值的强度，所以灰度级分辨率也叫辐射计量分辨率．
随着图像灰度级分辨率的逐渐降低，图像中包含的颜色数目变少，从而在颜色的角度造成图像信息受损，同样使图像细节表达受到一定影响，如图0.4所示．

数字图像处理与识别

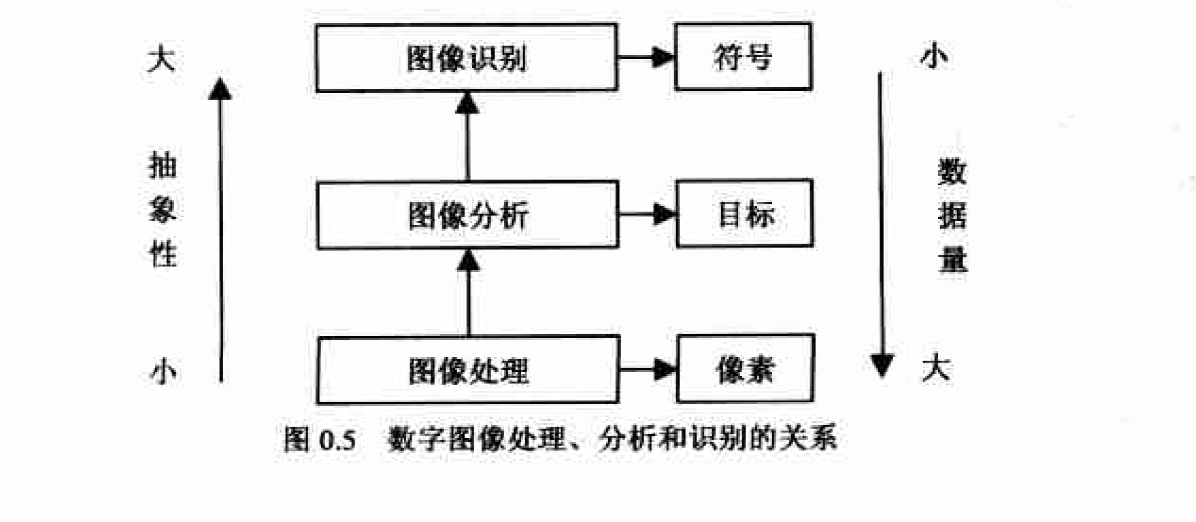
从信息论的角度而言， 图像应当是物体所含信息的 个概括， 而数字图像处理侧重于将这些概括的信息进行变换， 例如升高或降低娟值， 数字圈像分析则是将这些信息抽取出来以供其他过程调用． 当然， 在不太严格时， 数字图像处理也可以兼指图像处理和分析.
读者或许听过另一个概念，计算机图形学，此概念与数字图形分析大致相反，它是一个对由概念或数学表述的物体图像进行处理和显示的过程。

数字图像处理的预备知识

数字图像是由一组具有一定空间位置关系的像素组成， 因而具有一些度量和拓扑性质．
理解像素间的关系是学习图像处理的必要准备， 主要包括相邻像素， 邻接性、连通性，区域、
边界等概念，以及今后要用到的一些常见距离度量方法．另外0.3.3 小节还将简单介绍几种基
本的图像操作．

邻接性、连通性、区域和边界
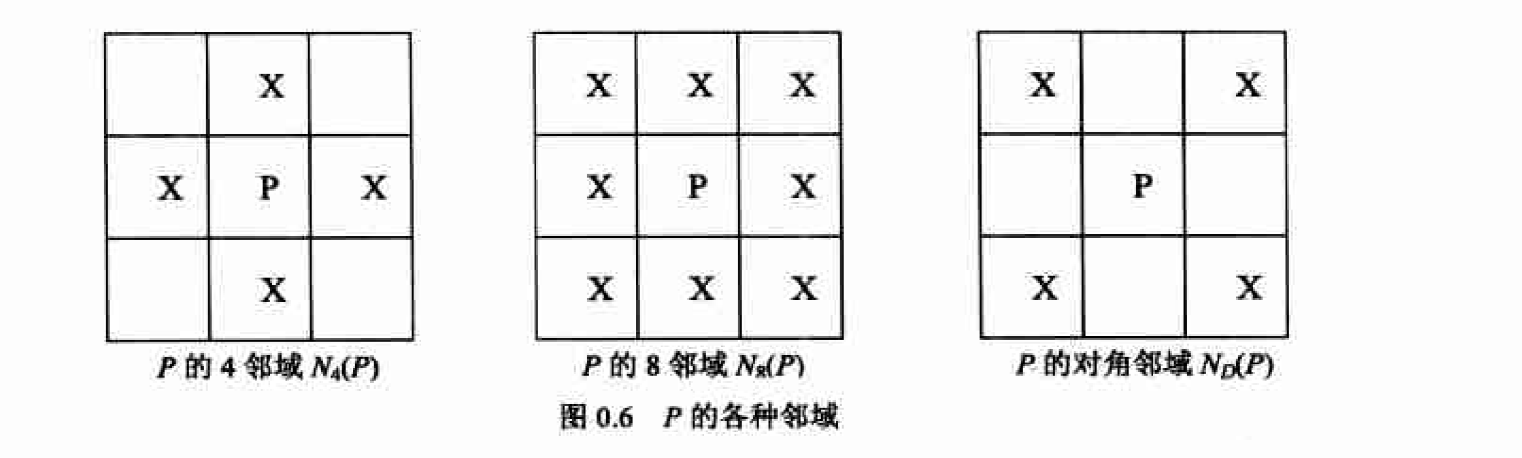
为理解上述这些概念， 需要首先了解相邻像素的概念。依据标准的不同， 我们可以关注
像素P的4邻域和8邻域， 如图0.6所示。

邻接性
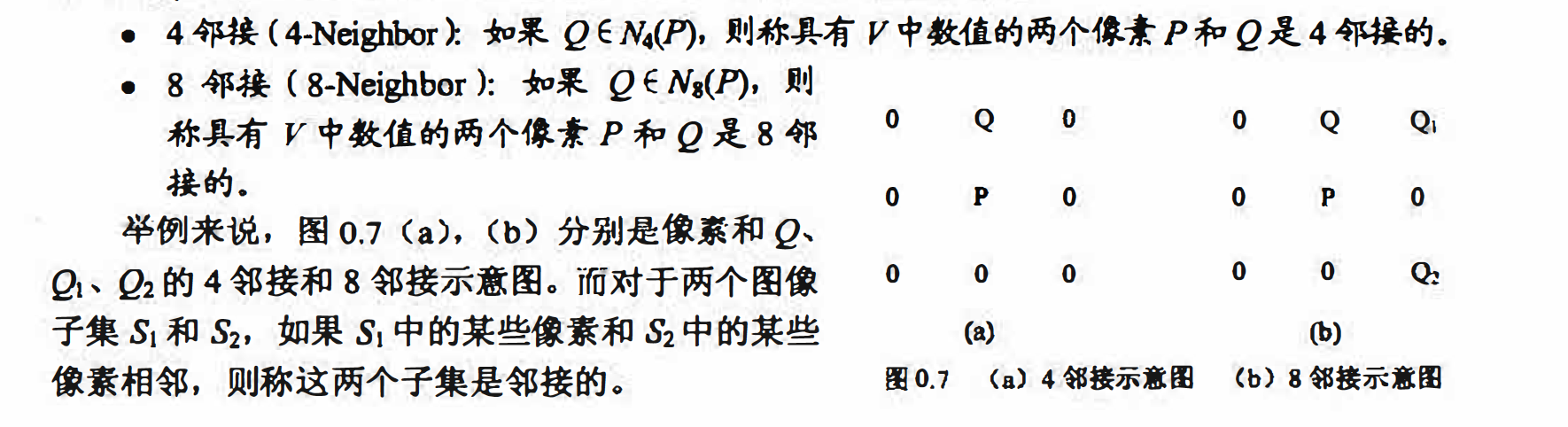
定义Y是用于决定邻接性的灰度值集合， 它是一种相似性的度量， 用于确定所需判断邻 接性的像素之间的相似程度。 比如在二值图像中， 如果我们认为只有灰度值为1的像素是相似的， 则V={l｝， 当然相似性的规定具有主观标准， 因此也可以认为扣｛O, l｝，此时邻接性 完全由位置决定：而对于灰度图像， 这个集合中则很可能包含更多的元素。 此外， 定义对角 邻域 $N_d(P）为8－邻域中不属于4－邻域的部分,那么

连通性

区域和边界
区域的定义建立在连通集的基础上的．令R是图像中的一个像素子集，如果R同时是连通集，则称R是一个区域.
边界的概念。是相对于区域而言的。一个区域的边界〈或边缘、轮廓〉是区域中所有包含一个或多个不在区域R中的邻接像素的像素所组成的集合．显然，如果区域R 是整幅图像，那么边界就由图像的首行、首列、末行和末列定义。因而，通常情况下，区域指一幅图像的子集，并·包括区域的边缘．而区域的边缘（Edge）则由具有某些导数值的像素组成，是一个像素及其直接邻域的局部性质，是一个有大小和方向属性的矢量。
边界和边缘是不同的。边界是和区域有关的全局概念，而边缘表示图像函数的局部性质

距离度量的几种方法

基本的图像操作

在后续章节中，将涉及各种各样的图像操作，这里以几种最为典型和常用的图像操作为例着重说明。按照处理图像的数量分类，可以分为对单幅图像操作〈如滤波〉和对多幅图像操作〈如求和、求差和逻辑运算等〉：按照参与操作的像素范围的不同，可以分为点运算和邻域运算：而根据操作的数学性质，又可以分为线性操作和非线性操作．

点运算和邻域运算

点运算指的是对图像中的每一个像素逐个进行同样的灰度变换运算．设r和s分别是输入图像f(x,y）和输出图像g(x,y）在任一点。(x，y）的灰度值，则点运算可以使用下式定义:

s=T(r)

如果将点运算扩展，对图像中每一个小范围〈邻域〉内的像素进行灰度变换运算，即称为邻域运算或邻域滤波。这可以使用下式定义：

g(x,y)=T[f(x,y)]

线性和非线性操作
令H是一种算子，其输入输出都是图像．若对于任意两幅〈或两组〉图像F1和F2及任意两个标量a和b都有如下关系成立:

H(aF1+bF2)=aH（F1）＋bH(F2)

则称H为线性算子。即对两幅图像的线性组合应用该算子与分别应用该算子后的图像在进行同样的线性组合所得到的结果相同，也就是说算子H满足线性性质。同样，不符合上述定义的算子即为非线性算子，对应的是非线性图像操作．举例来说，滤波中的平均平滑，高斯平滑，梯度锐化等都是线性运算，而中值滤波〈详见第5章＇＂空间域图像增强”〉则是非线 性的。

线性操作出于其稳定性的特点在图像处理中占有非常重要的地位。尽管非线性算子常常也能够提供较好的性能，但它的不可预测性使其在一些如军事图像处理和医学图像处理等严格的应用领域中难以获得广泛的应用。

算子

一般我们用字母M和N分别表示矩阵中的行与列。1x N
矩阵被称为行向量， M*1矩阵被称为列向量， 1*1矩阵则被称为标量。