傅立叶变换学习
空间域和频率域为我们提供了不同的视角. 在空域中. 函数的自变量(x, y)被视为二维空间中的一点, 数字图像J(x, y)即为一个定义在二维空间中的矩形区域上的离散函数:换一个角度, 如果将j(x, y)视为幅值变化的二维信号, 则可以通过某些变换手段(如傅立叶变
换、离散余弦变换、沃尔什变换和小波变换等〉在频域下对它进行分析.
本文主要包括以下内容
- 傅立叶变换的数学基础
- 快速傅立叶变换
- 本章的典型案例分析
- 美女与猫一-交换两幅图像的相位谱
频率域滤波一一与空间域滤波殊途同归
在多数情况下, 频率域滤波和空间域滤披可以视为对同一个图像增强问题的殊途同归的
两种解决方式. 而在另外一些情况下, 有些增强问题更适合在频域中完成(6.7节〉, 有些则
更适合在空域中完成. 我们常常根据需要选择是工作在空间域还是频率域, 并在必要时在这
两者之间相互转换.
傅立叶变换提供了一种变换到频率域的手段, 由于用傅立叶变换表示的函数特征可以完
全通过傅立叶反变换进行重建而不丢失任何信息, 因此它可以使我们工作在频率域而在转换
回空域时不丢失任何信息.
傅立叶变换在图像处理中的应用
理解了以下俩点:
- 图片是波,这个波可以看成N个正弦,余弦波的叠加
- 大自然中的各种信号的大部分信息都集中在低频,而且人眼对低频更敏感
就很容易明白傅立叶变换在图像处理中的应用。
- 在去噪上的原理和缺陷: 当图像出现的噪声是有规律的,相当于让某个频率波的幅度增大,把这个值减小,就是去掉这个频率的波,所以可以去噪,比如高斯噪声。当出现的噪声是没有规律的,随机出现的一些东西,FT是没有作用的。
- 在图片压缩方面,根据傅立叶变换推导出的DCT有很重要作用。JPEG格式的图片就是用Huffman编码方式压缩图片的DCT的系数。
傅立叶变换基础知识
通俗解释
到底什么是傅立叶级数
如何理解傅里叶变换公式?
如果看了此文你还不懂傅里叶变换,那就过来掐死我吧
傅立叶级数
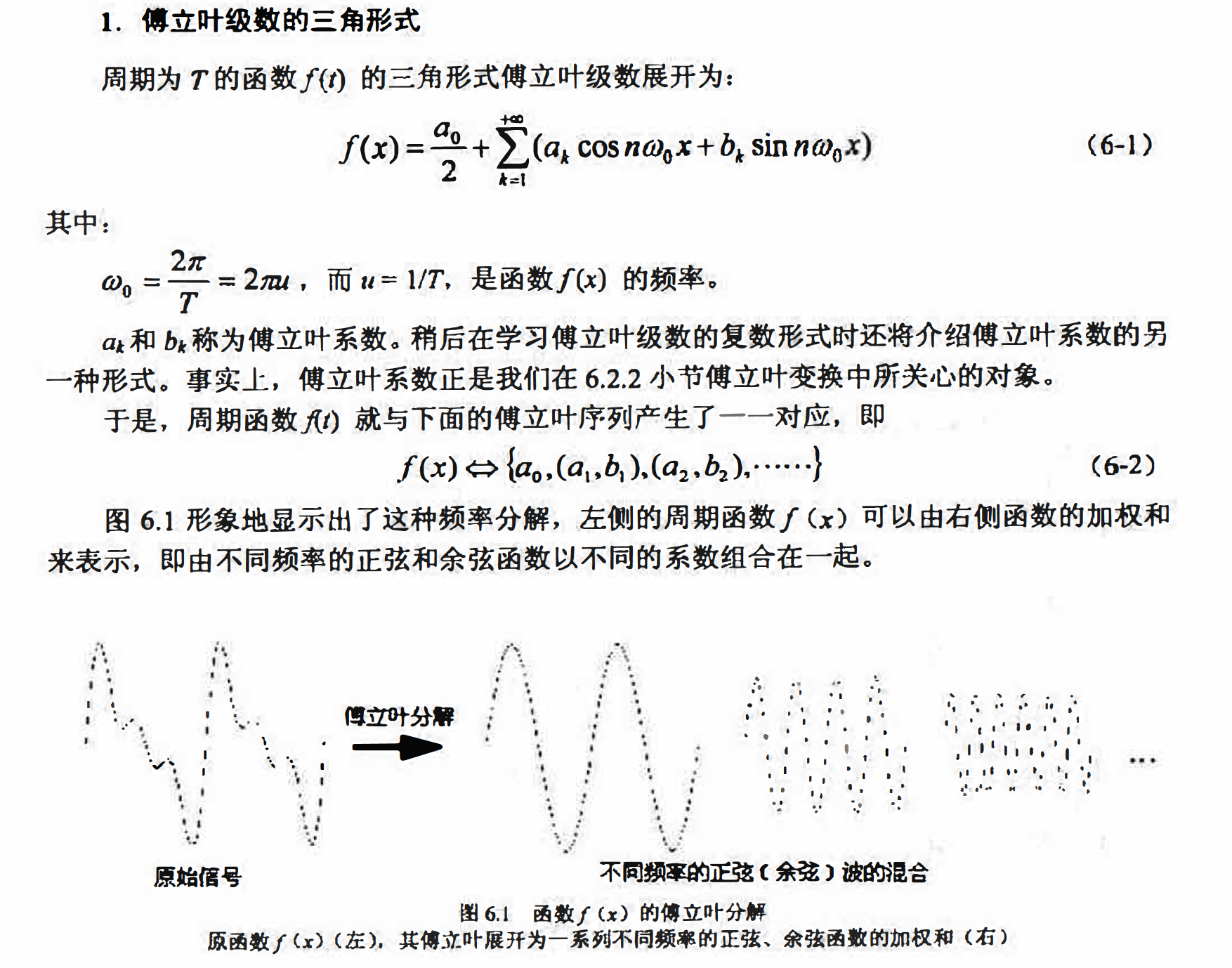
法国数学家傅立叶发现任何周期函数只要满足一定条件(狄利赫里条件〉都可以用正弦函数和余弦函数构成无穷级数,即以不同频率的正弦和余弦函数的加权和来表示,后世称为:傅立叶级数。
对于有限定义域的非周期函数,可以对其进行周期拓延从而使其在整个扩展定义域上为周期函数,从而也可以展开为傅立叶级数.

傅立叶级数的复指数形式
除上面介绍的三角形式外,傅立叶级数还有其他两种常用的表现形式,即余弦形式和复指数形式。借助欧拉公式,上述3种形式可以很方便地进行等价转化,本质上它们都是一样的。
复指数傅立叶级数即我们经常说的傅立叶级数的复数形式,因具有简洁的形式〈只需一个统一的表达式计算傅立叶系数〉,在进行信号和系统分析时通常令更易于使用:而余弦傅立叶级数可使周期信号的幅度谱和相位谱意义更加直观,函数的余弦傅立叶级数展开可以解释为f(x)可以由不同频率和相位的余弦披以不同系数组合在一起来表示,而在三角形式中相位是隐藏在系数Dn和bn中的。下面主要介绍复指数傅立叶级数,在后面的傅立叶变换中要用到的正是这种形式,关于余弦傅立叶级数的有关知识,感兴趣的读者请参考附录。
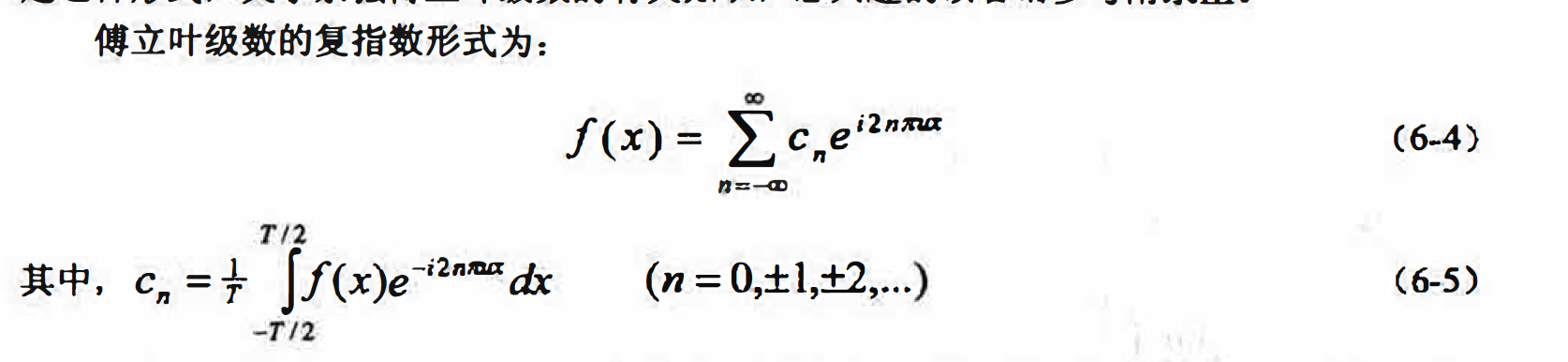
由式(6-4)和(6-5)可见,复指数傅立叶级数形式比较简洁,级教和系数都可以采用统一的公式计算.有关如何由式(6-1)推导出傅立叶级数复指数形式(6-4)的过程,由于这里我们感兴趣的井非傅立叶级数本身,因此不在正文中给出,详细的内容可参考附录。只要读者理解不同的展开形式其本质上是等价的,并对复指数形式的傅立叶级数展开建立了一个基本的形式上的认识就足以继续阅读和理解后述内容。
傅立叶变换

式(6-6)和式(6-7) 即为我们通常所说的傅立叶变换对,6.1节中提到的函数可以从它的反变换进行重建正是基于上面的傅立叶变换对。
由于傅立叶变换与傅立叶级数涉及两类不同的函数,在很多数字图像处理的书中通常对它们分别进行处理,并没有阐明它们之间存在的密切联系,这给很多初学者带来了困扰,实际上我们不妨认为周期函数的周期可以趋向无穷大,这样可以将傅立叶变换看成是傅立叶级数的推广。
仔细的观察式(6-6)和式(6-7),对比复指数形式的傅立叶级数展开公式〈式6-4), 可以发现这里傅立叶变换的结果F(u)实际上相当于傅立叶级数展开中的傅立叶系数,而反变换公式(式6-7) 则体现出不同频率复指数函数的加权和的形式,相当于复指数形式的傅立叶
级数展开公式,只不过这里的频率u变为连续化,所以加权和采用了积分的形式。这是因为随着式(6-5)的积分上下限的T向整个实数定义域扩展,即T→∞,频率u则趋近于du (因为u= 1/T),导致原来离散变化的u的连续化.



显然,这是f(x,y)各个像素的灰度之和。而如果将系数1/MN放在正变换之前, 则F(O, 0)对应于原因像f(x, y) 的平均灰度。F(O, 0)有时被称作频谱的直流分量(DC)。
我们之前曾指出一维函数可以表示为正弦〈余弦〉函数的加权和形式:类似的, 二维函数f(x,y)可以分解为不同频率的二维正弦〈余弦〉平面波的按比例叠加。
幅度谱、相位谱和功率谱


幅度谱又叫频率谐,是图像增强中关心的主要对象,频域下每一点(u,v)的幅度F(u,v)可用来表示该频率的正弦〈余弦)平面放在叠加中所占的比例,如图6.4所示.幅度谱直接反映频率信息,是频域滤波中的一个主要依据。
相位谱表面上看并不那么直观,但它隐含着实部与虚部之间的某种比例关系, 因此与图像结构息息相关。
因为对于和空域等大的频域空间下的每一点(u,v), 均可计算一个对应的|F(u,v)|和|U(u,v)|,所以可以像显示一幅图像那样显示幅度谱和相位谱。
冈萨雷斯版<图像处理>里面的解释非常形象:一个恰当的比喻是将傅里叶变换比作一个玻璃棱镜。棱镜是可以将光分解为不同颜色的物理仪器,每个成分的颜色由波长(或频率)来决定。傅里叶变换可以看作是数学上的棱镜,将函数基于频率分解为不同的成分。当我们考虑光时,讨论它的光谱或频率谱。同样, 傅立叶变换使我们能通过频率成分来分析一个函数。
Fourier theory讲的就是:任何信号(如图像信号)都可以表示成一系列正弦信号的叠加,在图像领域就是将图像brightness variation 作为正弦变量。比如下图的正弦模式可在单傅里叶中由三个分量编码:频率f、幅值A、相位γ 这三个value可以描述正弦图像中的所有信息。
图像的频率
直观上说,频率就是变化的快慢。傅立叶变换,把图像从空域变换到频域,在频率域中,高频分量表示图像中灰度变换比较快的那些地方,比如物体的边缘就是灰度的突然变化,所以物体边缘就是高频分量。而物体内部比较平坦的区域,灰度基本没有变化,对应的就是低频分量。
比如低通滤波只让低频分量通过,往往就是使图像模糊,因为边缘信息被去除了。
幅值magnitude(amplitude)
sin函数的幅值用于描述对比度,或者说是图像中最明和最暗的峰值之间的差。(一个负幅值表示一个对比逆转,即明暗交换。)
相位
相位表示相对于原始波形,这个波形的偏移量(左or右)
一个傅里叶变换编码是一系列正弦曲线的编码,他们的频率从0开始(即没有调整,相位为0,平均亮度处),到尼奎斯特频率(即数字图像中可被编码的最高频率,它和像素大小、resolution有关)。傅里叶变换同时将图像中所有频率进行编码:一个只包含一个频率f1的信号在频谱上横坐标f为f1的点处绘制一个单峰值,峰值高度等于对应的振幅amplitude,或者正弦曲线信号的高度。
DC term直流信号对应于频率为0的点,表示整幅图像的平均亮度,如果直流信号DC=0就表示整幅图像平均亮度的像素点个数=0,可推出 灰度图中,正弦曲线在正负值之间交替变化,但是由于灰度图中没有负值,所以所有的真实图像都有一个正的DC term,如上图所示。
出于某些数学分析原因,我们经常把傅里叶变换用mirror-image表示,在原点的的两端,frequency都是增加的方向,具有相同的幅值。
上面讲的都是一维信号,一个二维傅里叶变换是一维傅里叶变换在每一个行扫描线和列扫描线上的傅里叶变换的叠加。
傅里叶谱图上的每一个像素点都代表一个频率值,幅值由像素点亮度变码而得。最中心的亮点是指直流分量,傅里叶谱图中越亮的点,对应于灰度图中对比越强烈(对比度越大)的点。
由于每一列扫描线上没有变化,所以相应的fourier spectrum上行向量为0, 每一行扫描线上有contrast,所以有频率幅值。
图像傅立叶变换的物理意义
傅里叶提出任何周期函数都可以表示为不同频率的正弦和/或余弦和的形式,每个正弦和/或余弦乘以不同的系数(傅里叶级数)。图像的频率是表征图像中灰度变化剧烈程度的指标,是灰度在平面空间上的梯度.在噪声点和图像边缘处的频率为高频。
傅立叶变换在实际中有非常明显的物理意义,设f是一个能量有限的模拟信号,则其傅立叶变换就表示f的谱。从纯粹的数学意义上看,傅立叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看,傅立叶变换是将图像从空间域转换到频率域,其逆变换是将图像从频率域转换到空间域。换句话说,傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数,傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数.
傅立叶变换以前,图像(未压缩的位图)是由对在连续空间(现实空间)上的采样得到一系列点的集合,我们习惯用一个二维矩阵表示空间上各点,则图像可由z=f(x,y)来表示。由于空间是三维的,图像是二维的,因此空间中物体在另一个维度上的关系就由梯度来表示,这样我们可以通过观察图像得知物体在三维空间中的对应关系。为什么要提梯度?因为实际上对图像进行二维傅立叶变换得到频谱图,就是图像梯度的分布图,当然频谱图上的各点与图像上各点并不存在一一对应的关系,即使在不移频的情况下也是没有。傅立叶频谱图上我们看到的明暗不一的亮点,实际上图像上某一点与邻域点差异的强弱,即梯度的大小,也即该点的频率的大小(可以这么理解,图像中的低频部分指低梯度的点,高频部分相反)。一般来讲,梯度大则该点的亮度强,否则该点亮度弱。这样通过观察傅立叶变换后的频谱图,也叫功率图,我们首先就可以看出,图像的能量分布,如果频谱图中暗的点数更多,那么实际图像是比较柔和的(因为各点与邻域差异都不大,梯度相对较小),反之,如果频谱图中亮的点数多,那么实际图像一定是尖锐的,边界分明且边界两边像素差异较大的。对频谱移频到原点以后,可以看出图像的频率分布是以原点为圆心,对称分布的。将频谱移频到圆心除了可以清晰地看出图像频率分布以外,还有一个好处,它可以分离出有周期性规律的干扰信号,比如正弦干扰,一副带有正弦干扰,移频到原点的频谱图上可以看出除了中心以外还存在以某一点为中心,对称分布的亮点集合,这个集合就是干扰噪音产生的,这时可以很直观的通过在该位置放置带阻滤波器消除干扰.
图像是两个参数的函数,通过一组正交函数的线性组合可以将其分解,而傅里叶就是通过谐波函数来分解的。而对于离散傅里叶变换,傅里叶变换的条件是存在的
傅里叶变换进行图像处理有几个特点
1. 直流成分F(0,0)等于图像的平均值;
2. 能量频谱|F(u,v)|^2完全对称于原点;其中F=PfQ, f表示原图,P和Q都是对称的实正交矩阵,这个公式表示傅里叶变换就是个正交矩阵的正交变换
3.图像f平移(a,b)后,F只有exp[-2pij(au/M+bv/M)]的相位变化,能量频谱不发生变化。
4. 图像f自乘平均等于能量频谱的总和,f的分散等于能量频谱中除直流成分后的总和。
5.图像f(x,y)和g(x,y)的卷积h(x,y)=f(x,y)*g(x,y)的傅里叶变换H(u,v)等于f(x,y)和g(x,y)各自的傅里叶变换的乘积。
图像中的每个点通过傅里叶变换都成了谐波函数的组合,也就有了频率,这个频率则是在这一点上所有产生这个灰度的频率之和,也就是说傅里叶变换可以将这些频率分开来。当想除去图像背景时,只要去掉背景的频率就可以了。
参见:图像傅里叶变换
傅立叶变换的实质一基的转换
无论是傅立叶变换、离散余弦变换还是小波变换,其本质都是基的变换。
对于给定函数f(x),关键是选择合适的基,使得f(x)在这组基下的表现出我们需要的特性,当某一组基不满足要求时, 就需要通过变换将函数转换到另一组基下表示,方可得到我们需要的函数表示。 常用的变换有傅立叶变换〈以正弦和余弦函数为基函数〉、 小波变换〈以各种小波函数为基函数〉、 离散余弦变换以及Walsh变换等
快速傅立叶变换及其实现
6.2节介绍了离散傅里叶变换(DFT)的原理,但并没有涉及其实现问题,这主要是因为DFT的直接实现效率较低. 在工程实践中,我们迫切地需要一种能够快速计算离散傅立叶变换的高效算法,快速傅立叶变换(FFT)便应运而生.本节将给出快速傅立叶变换算法的原理及其实现细节.
FFT变换的必要性
这就是DFT的一种快速算法。
复数的加法乘法计算量很大,FFT利用了DFT中WN的周期性和对称性,把一个N项序列按奇偶分组,分为两个N/2项的子序列,继续分解,迭代下去,大大缩减计算量。具体算法就看那张蝶形图吧。
FFT对傅氏变换的理论并没有新的发现,但是对于在计算机系统或者说数字系统中应用离散傅里叶变换,可以说是进了一大步。
之所以提出快速傅立叶变换(FFT)方法,是因为在计算离散域上的傅立叶变换时. 对于N点序列,它的 DFT变换与反变换对定义为:


具体可参见: 十、从头到尾彻底理解傅里叶变换算法、上
Matlab实现
Matlab中提供了fft和ifft函数分别计算二维傅立叶变换和反变换,它们都经过了优化,速度很快:
另一个与傅立叶变换密切相关的函数是fftshft,常需要利用它来将傅立叶频谱图中的零频点移动到频谱图的中心位置

fftshit函数
fft2函数输出的频谱分析数据是按原始计算所得的顺序,来排列,而不是以零频为中心来排列,因此造成了零频在输频谱矩阵的角上,显示幅度谱图像时表现为4个亮度较高的角(零频处的幅值较高)
fftshift函数利用了频谱的周期性特点,将输出图像的一半平移到另一端,从而使零频被移动到图像的中间。其调用语法为:
Y = fftshift(X)
Y = fftshift(X,dim)dim指出了在多维数组的哪个维度上执行平移操作.

注意:在执行IFFT2函数之前,如果曾经使用FFTShift函数对频域图像进行过原点平移,则还需要4将原点平移回原位置.
I1 = imread('cell.tif');
fcoef = fft2(I1);
spectrum = fftshift(fcoef);
temp = log(1+abs(spectrum));
subplot(1,2,1);
imshow(temp,[]);
title('FFT');
subplot(1,2,2);
imshow(I1);
title('Source');
I2 = imread('circuit.tif');
fcoef = fft2(I2);
spectrum = fftshift(fcoef);
temp = log(1+abs(spectrum));
figure;
subplot(1,2,1);
imshow(temp,[]);
title('FFT');
subplot(1,2,2);
imshow(I2);
title('source');
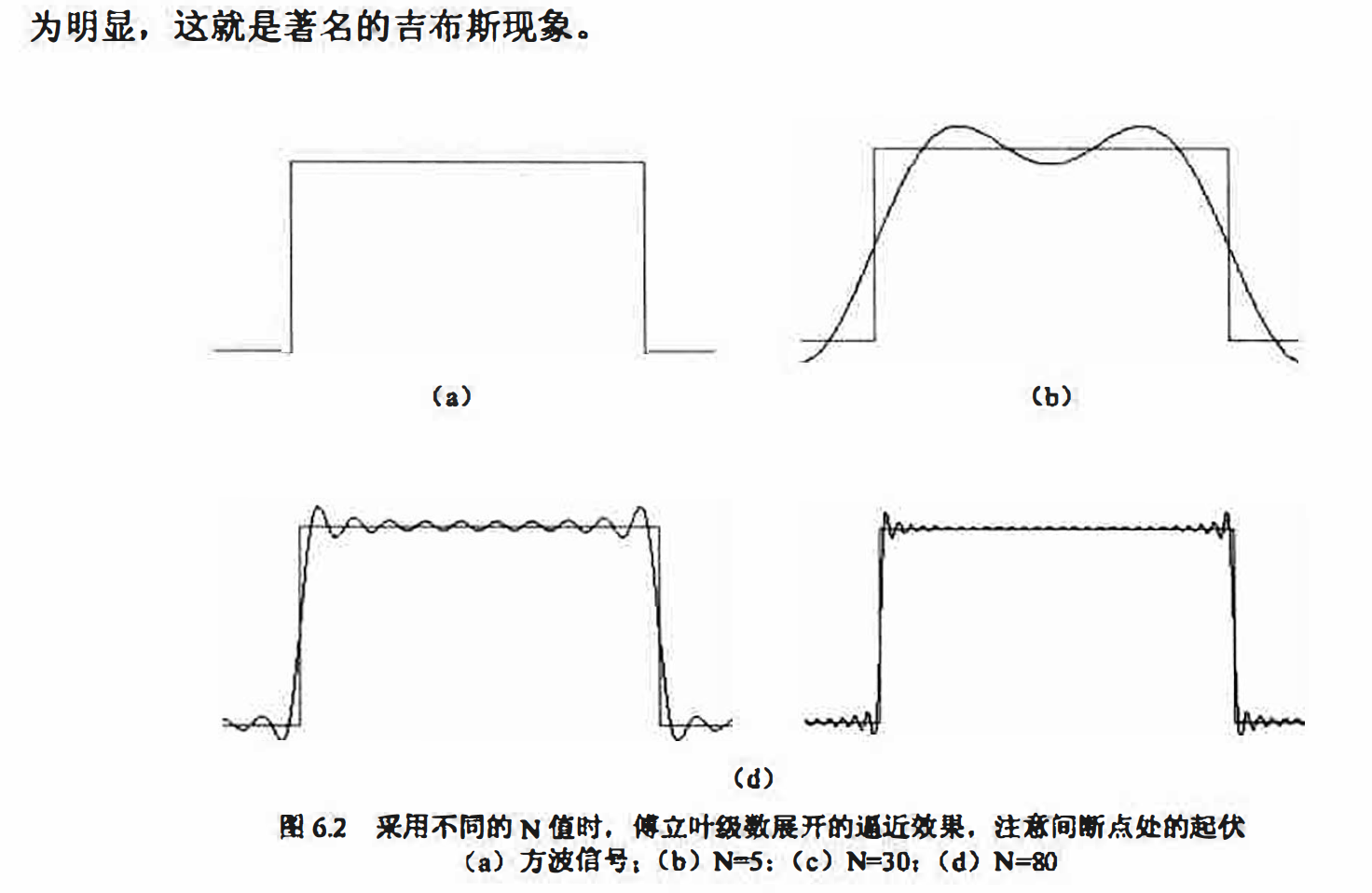
可以看出, 图(b)中的图像较为平滑, 而在其傅立叶频谱中,低频部分对应的幅值较大,而对(d)中细节复杂的的图像circuit.tif,灰度的变化趋势更加剧烈,相应的频谱中高频分量较强。
事实上,由于(b)图中基本只存在水平和垂直的线条,导致在输出的频谱中亮线集中存在于水平和垂直方向(并且经过原点〉。具体地说,原图像中的水平边缘对应频谱中的竖直亮线,而竖直边缘则对应频谱中的水平响应。我们不妨这样理解,水平方向的边缘可以看作在坚直方向上的灰度值的矩形脉冲,而这样的矩形脉冲可以分解为无数个竖直方向正弦平面波的叠加,从而对应频域图像中的垂直亮线:而对于竖直方向的边缘,情况类似。
通过例6.1,可以发现一些频谱与其空间域图像之间的联系.实际上,低频(频谱图像中靠近中心的区域〉对应图像的慢变化分量:高频〈频谱图像中远离中心的区域〉对应一幅图像中较快变化的灰度级, 常常对应图像细节, 如物体的边缘和噪声等。以图6.14 (c)的电
路图像为例,电路板的灰度较为一致的背景区域就对应着频谱的低频部分,而横竖电路线条的灰度变换则是相对高频的成份,且灰度变换越剧烈,就对应越高的频域分量.
美女与猫一一交换两幅图像的相位谱
图a,(b)中分别是一张美女的照片和一张猫的照片,这里我们准备交换这两幅
图像的相位谱,然用美女的幅度谱加上猫的相位谱,而用猫的幅度谱加上美女的相位谱,然
后根据式(6-18)通过幅度谱和相位谱来还原傅立叶变换F(u,v),再经傅立叶反变换得到文
又相位谱之后的图像. 根据6.2.2小节中关于幅度谱和相位谱各自作用的讨论,您能想到这样
做将会产生怎样的结果吗?
% c6s2.m
% 读取图片
A = imread('beauty.jpg');
B = imread('cat.jpg');
% 求傅立叶变换
Af = fft2(A);
Bf = fft2(B);
% 分别求幅度谱和相位谱
AfA = abs(Af);
AfB = angle(Af);
BfA = abs(Bf);
BfB = angle(Bf);
% 交换相位谱并重建复数矩阵
AfR = AfA .* cos(BfB) + AfA .* sin(BfB) .* i;
BfR = BfA .* cos(AfB) + BfA .* sin(AfB) .* i;
% 傅立叶反变换
AR = abs(ifft2(AfR));
BR = abs(ifft2(BfR));
% 显示图像
subplot(2,2,1);
imshow(A);
title('美女原图像');
subplot(2,2,2);
imshow(B);
title('猫的原图像');
subplot(2,2,3);
imshow(AR, []);
title('美女的幅度谱和猫的相位谱组合');
subplot(2,2,4);
imshow(BR, []);
title('猫的幅度谱和美女的相位谱组合');
通过这个示例可以发现, 经交换相位谱和反变换之后得到的图像内容与其相位谱对应的图像一致, 这就印证了我们之前关于相位谱决定图像结构的论断。 而图像中整体灰度分布特性, 如明暗、 灰度变化趋势等则在较大程度上取决于对应的幅度谱, 因为幅度谱反映了图像整体上各个方向的频率分量的相对强度。



