矩阵的特征值 => 矩阵的幂 => 广义斐波拉契数列的通项公式
众所周知,计算机里动辄涉及到斐波拉契数列,本文主要是运用线性代数的方法求出广义斐波拉契数列的通项公式。
广义斐波拉契数列的定义(自定义,可能还不够严谨,欢迎指教)如下:

且a,b满足a^2 + 4b > 0(原因后面有,即保证分母Δ>0)
观察递推公式可知:
 (1)
(1)



OK!写这篇博客有两点启示:
1.亦可用差分方程的方法求通项公式,不过我还没学,我发现把递推关系用矩阵的形式写成再求通项也是可以的,不过要构造出这个关系比较困难,比如(1)式。
2.在一般的算法中求矩阵的幂几乎都是用二分法求,殊不知若λi下有ki个线性无关的特征向量(ki是λi的重根数),即可用相似对角形的方法求,这在高等数学里可是小儿科。虽然前面的步骤有点繁,但作用是“磨刀不误砍柴工”,直接手算矩阵的幂。
2012/4/7更新:
今天发现递推公式可简化为:
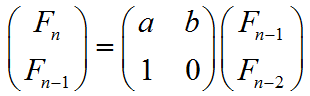
这样算起来更方便!
2012/4/15更新:
想要更刺激的吗?好吧,直接来个n阶的!

From: Fibonacci数计算中的两个思维盲点及其扩展数列的通用高效解法
持续更新中 ing
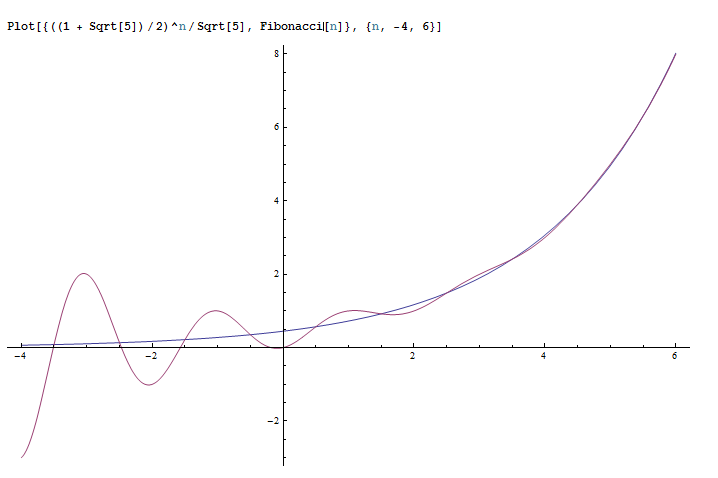
附:上一张关于菲波拉契数列的图:Fib与指数爆炸

 浙公网安备 33010602011771号
浙公网安备 33010602011771号