如何求平方根 - Algorithm 第四版 - 读书笔记

如何求平方根

假如以我们人脑的思考方式去思考求8的开方，由于我们知道2的平方为4，3的平方为9，所以我们可以用2.X去猜测，由于2.9的平方大于8，2.8的平方小于8，所以十分位确定了，然后我们再去按照同样的方式去思考下一位。这样一点点的去求得接近8的开方值的数据，直到我们达到需要的精度，比如保留三位小数就是2.828。

那如果以机器的角度去计算呢？答案当然也是猜，只是说以某个默认值去猜测然后逐步的接近目标值，然后也是达到需要的精度就停止。

那具体如何求解呢

有一个求解方法叫做牛顿-拉弗森方法，也叫做牛顿迭代法，这个方法基于一个很好理解的定理：切线是曲线的线性逼近，具体如下图A。

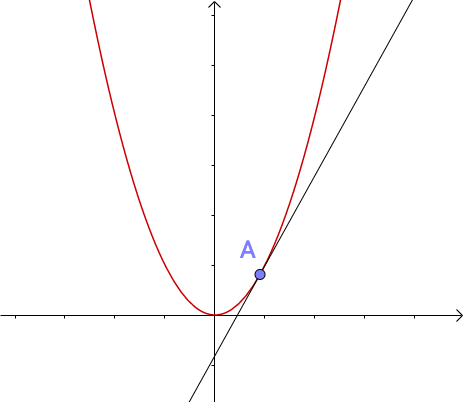
图A

如果我们将图A的A处放大就可以得到下图B：

 

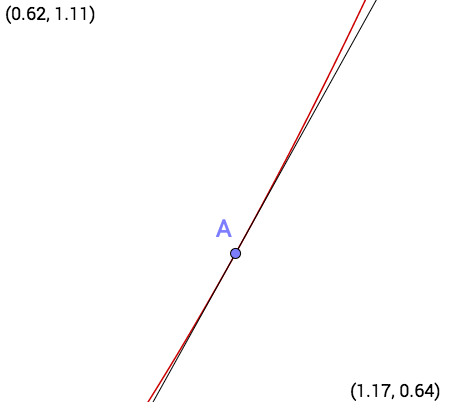
图B

 可以看到图B的A点处的切线与曲线十分的接近，而切线是直线，是线性的，所以可以说A点处的切线是f（x）的线性逼近，也就是在A点附近的切线应该是约等于f（x）的。

那么利用这一点直觉

对于果求a值的开方，首先我们随便找一个近似的x值（可以直接默认为a），如果我们不断利用（ x1，f（x1））位置的切线去逼近曲线 x^2 - a = 0 就可以去逐步接近真正的开方值，直到我们需要的精度。

那么如何去逼近呢？

根号a是 x^2 = a 的一个正实根，而这个函数（ x^2 = a ）的导数为2x，所以说函数上的点（ x1，f（x1））的切线斜率都为2，所以（ x1，f（x1））处的切线方程为：f（x1）+ 2(x -x1) 。 所以 x - f (x) /（2x）就是一个比x更接近答案的近似值，带入f（x）= x^2 就可以得到新的近似值 = （x + a/x）/2。

有兴趣的话可以看看这个视频：牛顿求根法

代码实现

class SqureRoot {
    public static double sqrt(double c) {
        if (c < 0) return Double.NaN;
        double err = 1e-15;
        double t = c;
        while (Math.abs(t - c/t) > err * t)
            t = (c/t + t) / 2.0;
        return t;
    }
    
    public static void main(String[] args) {
　　　　System.out.printf("Squre root of %f is %f",8.0,sqrt(8));

    }
}

output：

Squre root of 8.000000 is 2.828427