最大连续子数组 - Maximum Subarray - Leetcode -easy

题目

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

I/O 栗子

Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
解释: [4,-1,2,1] 为拥有最大和的连续子数组，对应和为6.

Input: nums = [1]
Output: 1

Input: nums = [-2147483647]
Output: -2147483647

约束条件

• 1 <= nums.length <= 2 * 10^4
• -2^31 <= nums[i] <= 2^31 - 1

解法1 动态规划

利用动态规划方法，可以在线性时间内求解，整体思路是利用固定大小滑动窗口的和来解决这个问题，沿数组移动并修改数组本身，这样的好处是不会有额外的空间占用，为什么要修改数组本身？因为修改数组可以在此得出给定点当前的局部最大和。下一步是在知道局部最大值的情况下更新全局的最大值。

借用一张图找到的图来解释：

当上一位为正数，则本位更新为上一位+本位

我的代码 

    public int maxSubArray(int[] nums) {
        int max = nums[0];
        for(int i = 1 ; i < nums.length ; ++i){
            if(nums[i-1] > 0) {
                nums[i] += nums[i-1];
            }
            if(nums[i] > max) max = nums[i];
        }
        return max;
    }

复杂度解析

• 时间复杂度：O（N），因为只遍历了一边数组。
• 空间复杂度：O（1），占用恒定的nums原本的空间。

解法2 分治法

根据解决分治问题的解决方案模板：

• 定义基本案例。

• 将问题分解为子问题，然后递归解决。

• 合并子问题的解决方案以获得原始问题的解决方案

解决方案

• 如果n == 1：返回此单个元素。

• left_sum=左子数组的maxSubArray， 即第一个n/2数字（索引处的中间元素(left + right) / 2始终属于左子数组）。

• right_sum= maxSubArray用于右边的子数组， 即最后的n/2数字。

• cross_sum=包含来自左右子数组的元素的子数组的最大总和，因此越过索引处的中间元素 (left + right) / 2。

• 合并子问题解决方案，即 return max(left_sum, right_sum, cross_sum)

虽然这个方法写下来不是那么简单但个人觉得更符合人的思考逻辑，用下图来进行理解：

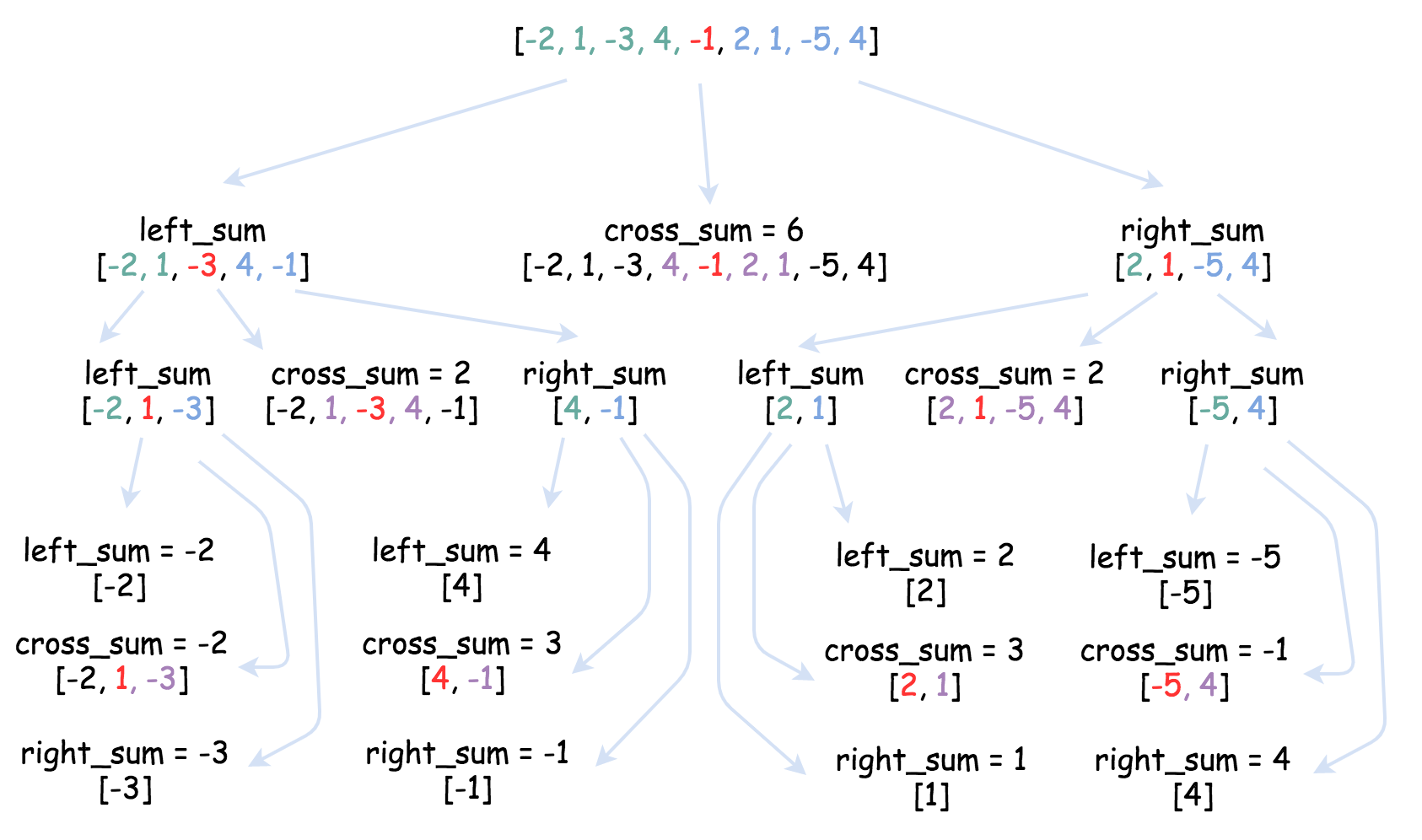
类似快排或者归并排序的思路

我的代码 

  public int crossSum(int[] nums, int left, int right, int p) {
    if (left == right) return nums[left];

    int leftSubsum = Integer.MIN_VALUE;
    int currSum = 0;
    for(int i = p; i > left - 1; --i) {
      currSum += nums[i];
      leftSubsum = Math.max(leftSubsum, currSum);
    }

    int rightSubsum = Integer.MIN_VALUE;
    currSum = 0;
    for(int i = p + 1; i < right + 1; ++i) {
      currSum += nums[i];
      rightSubsum = Math.max(rightSubsum, currSum);
    }

    return leftSubsum + rightSubsum;
  }

  public int helper(int[] nums, int left, int right) {
    if (left == right) return nums[left];

    int p = (left + right) / 2;

    int leftSum = helper(nums, left, p);
    int rightSum = helper(nums, p + 1, right);
    int crossSum = crossSum(nums, left, right, p);

    return Math.max(Math.max(leftSum, rightSum), crossSum);
  }

  public int maxSubArray(int[] nums) {
    return helper(nums, 0, nums.length - 1);
  }

复杂度解析

• 时间复杂度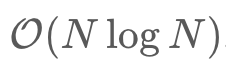：，因为只遍历了一边数组。

• 空间复杂度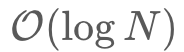： ，利用递归调用的栈进行数据存储，广度为N，则log2N层的栈空间消耗。 

 以上内容为做题时候的自行总结，如有不对，感谢指正。