ID3算法:
自顶向下分裂属性
依据信息熵 \(entropy(D)=-\sum_{i=1}^kp(c_i)log_2p(c_i)\)
其中D为数据集,类别\(C=\{c_1,c_2,...c_k\}\)
\(count(c_i)\):\(c_i\)出现在数据集D中的次数,\(|D|\):数据集D的个数
\(p(c_i)\):\(c_i\)在D中出现的相对频率即:\(p(c_i)=count(c_i)/|D|\)
以属性A分裂后的数据集的信息熵\(entropy(D,A)=-\sum_{i=1}^k\frac{|D_i|}{|D|}entropy(D_i)\)
信息增益\(gain(D,A)=entropy(D)-entropy(D,A)\)
每次选择以最优的信息增益分裂决策树
ID3的改进,C4.5算法:
增加了信息增益比并取代了信息增益进行选择:
\(gain_{ratio}(D_A)=\frac{gain(D,A)}{splitInfo(D,A)}=\frac{gain(D,A)}{-\sum_{i=1}^m\frac{|D_i|}{|D|}log_2( \frac{|D_i|}{|D|} )}\)
自动对连续属性离散化(数值区间划分成能够得到最小熵的点,比如按每次增加100计算最后最优划分点)
自动剪枝防止过度拟合
举个例子:
| 西瓜 | 重量/g | 颜色 | 质量 |
|---|---|---|---|
| 西瓜1 | 1000 | 绿色 | 好 |
| 西瓜2 | 1200 | 黑色 | 不好 |
| 西瓜3 | 1900 | 绿色 | 不好 |
| 西瓜4 | 2300 | 绿色 | 好 |
| 西瓜5 | 2000 | 绿色 | 好 |
| 西瓜6 | 1800 | 绿色 | 不好 |
| 西瓜7 | 1700 | 绿色 | 不好 |
第一步计算数据集信息熵:好的3个,不好的4个
\(entropy(D)=-\sum_{i=1}^kp(c_i)log_2p(c_i)=−\frac{3}{7}log_2 (\frac{3}{7})−\frac{4}{7}log_2 (\frac{4}{7})=0.985\)
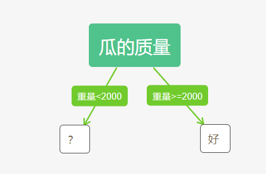
属性重量以2000划分>=2000 2个和<2000 5个 (数据离散化,1000,2300区间找划分能够得到最小熵的点,比如按每次增加100计算最后取最优,这里随机找了2000)
计算信息增益:
\(entropy(D,重量)=-\sum_{i=1}^k\frac{|D_i|}{|D|}entropy(D_i)=-\frac{2}{2}log_2(\frac{2}{2})-\frac{0}{2}log_2{0}{2}-\frac{1}{5}log_2(\frac{1}{5})-\frac{4}{5}log_2(\frac{4}{5})=0.722\)
\(gain(D,重量)=entropy(D)-entropy(D,重量)=0.263\)
\(entropy(D,颜色)=-\sum_{i=1}^k\frac{|D_i|}{|D|}entropy(D_i)=-\frac{1}{1}log_2(\frac{1}{1})-\frac{0}{1}log_2{0}{1}-\frac{2}{6}log_2(\frac{2}{6})-\frac{4}{6}log_2(\frac{4}{6})=0.918\)
\(gain(D,颜色)=entropy(D)-entropy(D,颜色)=0.067\)
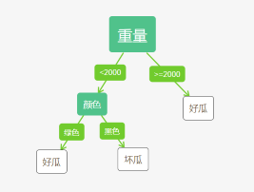
计算\(gain_{ratio}\)得\(gain_{ratio}(D,重量)>gain_{ratio}(D,颜色)\),故先分裂重量