C语言函数与宏定义实验报告
C语言函数与宏定义实验报告
姓名:揭子奇 实验地点:一教524 实验时间:2021-5-18
一、实验目的与要求
1、掌握函数的定义方法和调用规则。
2、掌握在C语言程序中主调函数和被调函数之间进行数据传递的规则。
3、了解函数的返回值及其类型,并正确使用。
4、了解局部变量和全局变量的作用城及它们与存做分类的关系,理解变量的存在性和可见性的概念
二、实验内容
实验一:6.3
1、问题描述:
编写程序,从键盘输入三角形的三条边,调用三角形面积函数求出其面积,并输出结果。
2、实验代码:
#include <stdio.h>
float area(float a,float b,float c)
{
float s,p,area;
s=(a+b+c)/2;
p=s*(s-a)*(s-b)*(s-c);
area=sqrt(p);
return(area);
}
void main()
{
float a,b,c,ts;
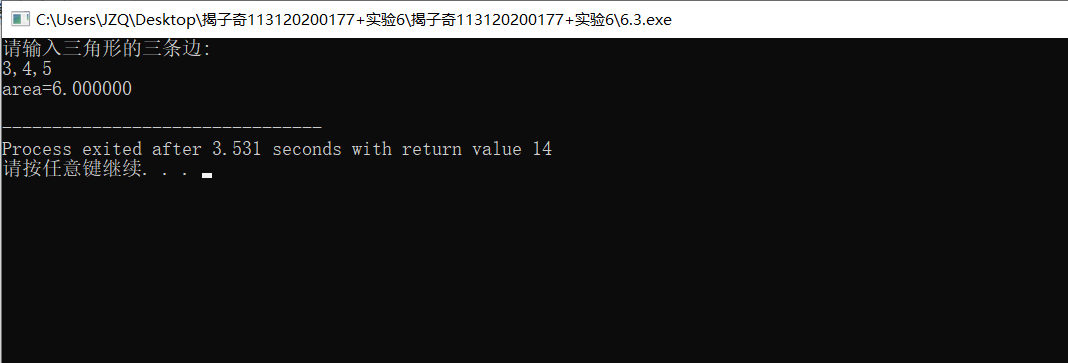
printf("请输入三角形的三条边:\n");
scanf("%f,%f,%f",&a,&b,&c);
ts=area(a,b,c);
if(a+b>c&&a+c>b&&c+b>a)
printf("area=%f\n",ts);
else
printf("Data error!");
}
3、问题分析
需注意所求面积的类型是浮点型,有返回值,不能写成调用语句,而应把函数调用当作表达式。
实验二:6.5
1、问题描述:
从键盘输入两个整数,调用gcd()函数求它们的最大公约数,并输出结果。
2、实验代码:
int remainder;
if(a<b)
{
temp=a;
a=b;
b=temp;
}
loop:
remainder=a%b;
while(remainder!=0)
{
a=b;
b=remainder;
goto loop;
}
return b;
}
void main()
{
int a,b;
int fac;
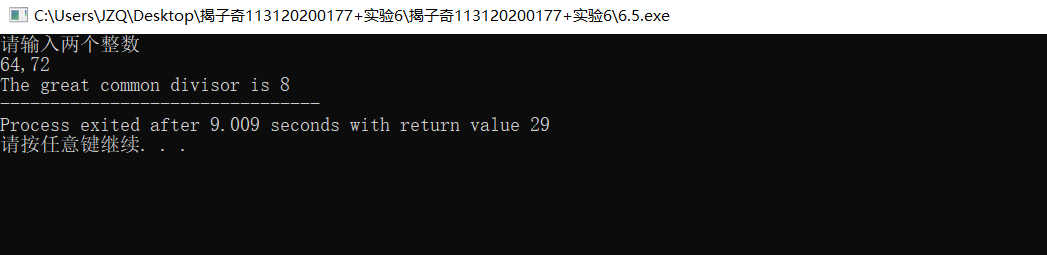
printf("请输入两个整数\n") ;
scanf("%d,%d",&a,&b);
fac=gcd(a,b);
printf("The great common divisor is %d",fac);
}
3、问题分析:
程序的关键点是用辗转相除法求两个整数的最大公约数。
实验三:6.7
1、问题描述:
求所有500以内的定义的亲密数
2、实验代码:
int facsum(int m)
{
int sum=1,f;
for(f=2;f<=m/2;f++)
{
if(m%f==0)
sum=sum+f;
}
return sum;
}
void main()
{
int m,n,k;
for(m=3;m<=500;m++)
{
n=facsum(m);
k=facsum(n);
if(m==k&&m<=n)
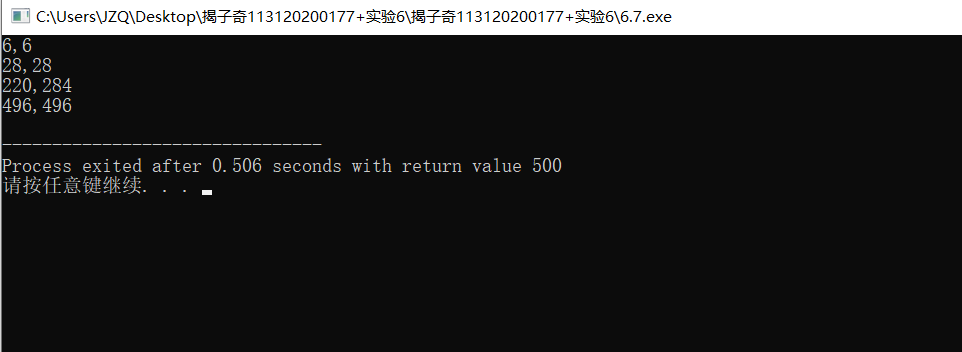
printf("%d,%d\n",m,n);
}
}
3、问题分析:
程序关键点在于先把一个数的因子累加,再把求出来的因子作为返回值,看返回后的第二个因子是否和之前的因子相等。
实验四:6.9
1、问题描述:
编制计算Ackerman函数的递归函数Ack(n,x,y)
2、实验代码:
int Ack(int n,int x,int y)
{
int a;
if(n==0)
a=x+1;
else if(n==1&&y==0)
a=x;
else if(n==2&&y==0)
a=0;
else if(n==3&&y==0)
a=1;
else if(n>=4&&y==0)
a=2;
else
{
a=Ack(n-1,Ack(n,x,y-1),x);
}
return a;
}
void main()
{
int n,x,y,result;
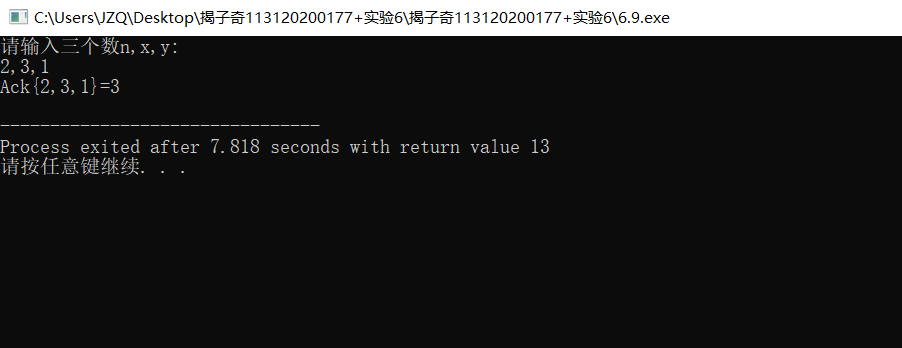
printf("请输入三个数n,x,y:\n");
scanf("%d,%d,%d",&n,&x,&y);
if(n>=0&&x>=0&&y>=0)
{
result=Ack(n,x,y);
printf("Ack{%d,%d,%d}=%d\n",n,x,y,result);
}
else
printf("请输入三个非负整数!");
}
3、问题分析:
本题关键在于你要利用好多个if-else嵌套来实现计算条件的判断,有五个回归条件
三、什么是辗转相除法
辗转相除法, 又名欧几里德算法(Euclidean algorithm),是求最大公约数的一种方法。它的具体做法是:用较大数除以较小数,再用出现的余数(第一余数)去除除数,再用出现的余数(第二余数)去除第一余数,如此反复,直到最后余数是0为止。https://zhidao.baidu.com/question/156706020.html
四、实验小结
本实验了解到了很多新型的算法,同时还练习熟悉了函数的定义和调用,不足之处为对用法还不够熟练,还要多加练习
五、近期个人学习小结
本学期学到了很多相关知识点,比如循环结构、判断结构和函数定义与调用等等,其中还存都在一些问题,今后还需要多加完善、巩固和学习





