数据结构（十）：复杂图-加权有向图，最短路径
一、 加权有向图概述
加权有向图是在加权无向图的基础上，给边添加了方向，并且一条加权有向边只会在一个顶点的邻接表中出现。
二、 加权有向图实现
为了体现边的有向性，我们需要知道边的起点和终点，参照如下来构建有向边，而有向图的构建只需在前面无向图的基础上，将无向边对象更换为有向边对象即可
|
/** * 有向边对象 * @author jiyukai */ public class DirectedEdge {
//有向边起点 private int v;
//有向边终点 private int w;
//有向边权重 private double weight;
public DirectedEdge(int v, int w, double weight) { super(); this.v = v; this.w = w; this.weight = weight; }
/** * 起点 * @return */ public int from() { return v; }
/** * 终点 * @return */ public int to() { return w; }
/** * 有向边权重 * @return */ public Double weight() { return weight; } } |
|
import com.data.struct.common.list.queue.Queue;
/** * 有向图实现 * @author jiyukai */ public class Digraph {
//定点个数 public int V;
//边的数量 public int E;
//图的邻接表 public Queue<DirectedEdge>[] qTable;
public Digraph(int v) { this.V = v;
this.E = 0;
//初始化邻接表，数组中的索引为顶点，值为已队列，存放相邻的顶点 qTable = new Queue[v]; for(int i=0;i<v;i++) { qTable[i] = new Queue<DirectedEdge>(); } }
/** * 向图中添加一条有向边 * @param v * @param w */ public void addEdge(DirectedEdge e) {
//获取边的起点 int v = e.from();
//起点到终点的指向 qTable[v].enqueue(e);
//边加1 E++; }
/** * 返回当前顶点的数量 * @return */ public int V() { return V; }
/** * 返回当前边的数量 * @return */ public int E() { return E; }
/** * 获取与顶点V相邻的顶点 * @param V * @return */ public Queue<DirectedEdge> adjoin(int V) { return qTable[V]; }
/** * 获取加权有向图的所有边 * @return */ public Queue<DirectedEdge> directEdges(){ Queue<DirectedEdge> diedges = new Queue<DirectedEdge>();
//由于有向图中，有向边只存在一个顶点的邻接表中，不存在相同边出现在不同顶点的邻接表中的情况，所以遍历添加即可 for(int v=0;v<V;v++) { for(DirectedEdge e : qTable[v]) { diedges.enqueue(e); } }
return diedges; } } |
三、 最短路径
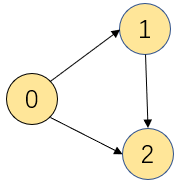
最短路径用来在加权有向图中，寻找顶点v到顶点w经过的有向边的最短路径，如下为一幅加权的有向图，各边的指向和权限已在图和表格中标出，红色边即为顶点0到顶点4经过的最短路径。
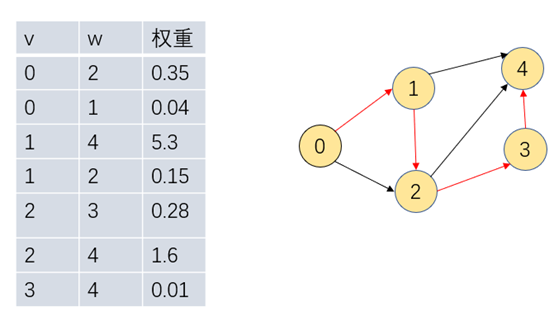
四、 松弛思想和Disjstra实现思路
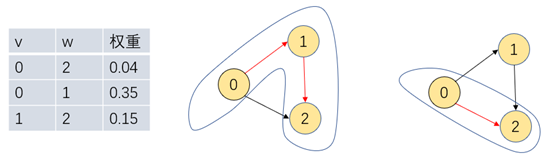
那么如何在一副有向图中求得最短路径呢，这里我们用到了一种思想叫松弛思想，如下图
同样是顶点0到顶点2的路径，图一的蓝色边框看做皮筋，那么皮筋圈住的距离是0.35+0.15=0.5，图二的蓝色边框看做皮筋，那么皮筋圈住的距离是0.04，同样是起点为0，终点为2
我们把图一的皮筋改成图二后，皮筋很明显的松弛了，即在松弛状态下达到了和图一一样的效果。
这种松弛的原理和方法可以用来解决最短路径的问题，我们在算最短路径时，需要有个数组edges[]存放当前顶点和上一个顶点的最短边，索引为顶点，值为边
edgesWeight[]存放起点s到其他顶点的权重之和，还有一个索引优先队列minQueue存放最短路径到各个顶点的有效最短边。
松弛：
原路径顶点0到顶点3放松到边4-3，意味着需要判断顶点0到顶点3的最短路径是否从0-4，再从4-3，从如下图来看若放松到4-3，则最小路径变成了7.2+1.1=8.3>4.5，所以这时忽略放到4-3的请求。
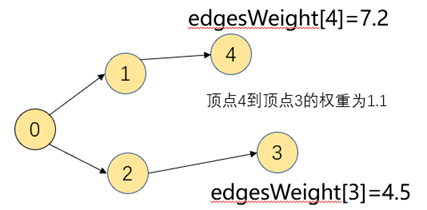
从如下图来看若放松到4-3，则最小路径变成了0.6+1.1=1.7<4.5，所以这时需要将4-3添加到edges[3]的最小路径边中，同时更改edgesWeight[3]=1.7
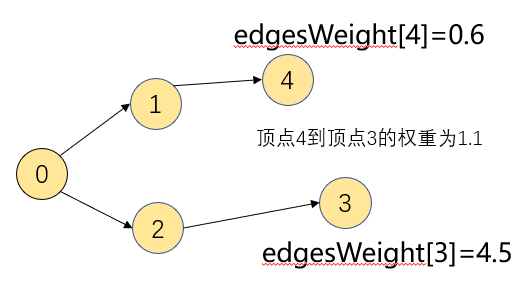
如下通过一个简单的过程来演示找到一副图中的最短路径，初始化状态如下
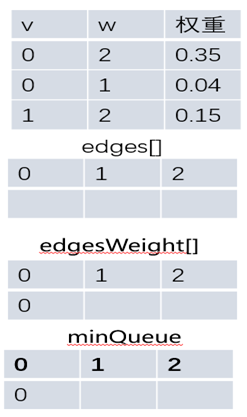
步骤一：遍历起点0的邻接边，找到最短的边0-1添加到最短路径中，同时加入到edges数组中，并将0到1的权重之和添加到edgesWeight[]数组中，修改顶点0到各个顶点的有效横切边minQueue。
步骤二：遍历0和1组成的最短路径的邻接边，通过比较0-2的距离0.35>0-1,1-2的距离0.19，找到最短路径1-2加入到最短路径中，并同时修改edges[]数组和edgesWeight数组
修改顶点0和1组成的最短路径到各个顶点的有效横切边minQueue。
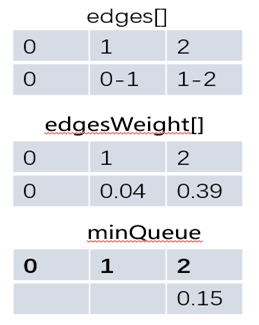
步骤三：找起点v到w的最短路径时，只需从edges数组逆向查找即可，比如查找0-2的最短路径，首先获取edges[2]，然后通过边对象取到2的起点1，找到edge[1]，依次找到起点0
则可以发现最短路径为0-1,1-2
五、 Disjstra代码实现
|
import com.data.struct.common.list.queue.Queue; import com.data.struct.common.tree.priority.queue.IndexMinPriorityQueue;
/** * Dijkstra算法实现 * @author jiyukai */ public class DijkstraSP {
// 存放当前顶点和上一个顶点的最短边，索引为顶点，值为边 private DirectedEdge[] edges;
// 存放起点s到其他顶点的权重之和 private double[] edgesWeight;
// 存放最小生成树顶点与非最小生成树顶点的目标横切边，索引为顶点 private IndexMinPriorityQueue<Double> minQueue;
public DijkstraSP(Digraph G, int s) throws Exception {
edges = new DirectedEdge[G.V()]; edgesWeight = new double[G.V()];
// 初始化时将edgesWeight的值暂时设置为无穷大，起点处设置为0 for (int i = 0; i < edgesWeight.length; i++) { edgesWeight[i] = Double.POSITIVE_INFINITY; } edgesWeight[0] = 0.0;
minQueue = new IndexMinPriorityQueue<>(G.V()); minQueue.insert(0, 0.0);
while (!minQueue.isEmpty()) { // 松弛图G中的顶点 relax(G, minQueue.delMin()); }
}
/** * 进行松弛操作 * @param g * @param delMin * @throws Exception */ private void relax(Digraph G, int v) throws Exception { // 首先遍历顶点的邻接边 for (DirectedEdge e : G.qTable[v]) { // 获取边的终点 int w = e.to();
// 起点到顶点w的权重是否大于起点到顶点v的权重+边e的权重 // 如果大于，则修改s->w的路径,edges[w]=e,并修改edgesWeight[v] = // edgesWeight[v]+e.weight(),如果不大于,则忽略 if (edgesWeight[v] + e.weight() < edgesWeight[w]) {
edges[w] = e; edgesWeight[w] = edgesWeight[w] + e.weight();
// 如果顶点w已经存在于优先队列minQueue中，则重置顶点w的权重 if (minQueue.contains(w)) { minQueue.changeItem(w, edgesWeight[w]); } else { // 如果顶点w没有出现在优先队列pq中，则把顶点w及其权重加入到pq中 minQueue.insert(w, edgesWeight[w]); } } } }
/** * 判断从顶点s到顶点v是否可达 * @param v * @return */ public boolean hasPathTo(int v) { return edgesWeight[v] < Double.POSITIVE_INFINITY; }
/** * 逆向查询从起点s到顶点v的最短路径中所有的边 * @param v * @return */ public Queue<DirectedEdge> pathTo(int v){ Queue<DirectedEdge> minPaths = new Queue<>();
//不存在连通的路径，则返回null if(!hasPathTo(v)) { return null; }
//逆向查找过程 DirectedEdge e = null;
while(true){ e = edges[v]; if(e==null) { break; }
minPaths.enqueue(e); v = e.from(); }
return minPaths; } } |
