数据结构（十）：复杂图-加权无向图，最小生成树
一、 加权无向图概述
加权无向图是在无向图的基础上，为每条无向边关联一个成本或是权重值。
在导航中，我们常常需要判断图中由若干边组成的路径是否是长度最短，时间最短或是通行成本最低，权重不一定表示距离，可以多样化的表示为跟成本相关的数据。
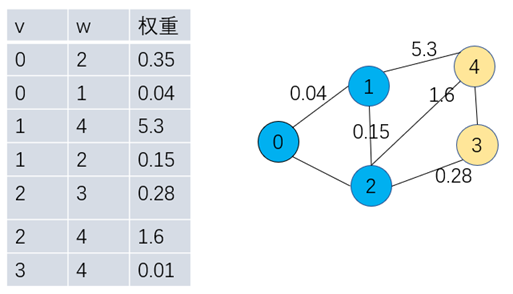
二、 加权无向图实现
由于无向图的边关联了权重，因此需要把边作为一个对象处理，包含两个顶点和边的权重三个重要属性，具体实现如下
|
/** * 加权无向图的边对象 * @author jiyukai */ public class Edge implements Comparable<Edge>{
//边的顶点1 private int v;
//边的顶点2 private int w;
//边的权重 private int weight;
public Edge(int v, int w, int weight) { super(); this.v = v; this.w = w; this.weight = weight; }
/** * 获取边的权重 * @return */ public int getWeight() { return weight; }
/** * 获取顶点 * @return */ public int getV() { return v; }
/** * 获取v顶点外的另一个顶点 * @return */ public int getEither(int k) { //顶点与v相等，则返回另一个 if(k==v) { return w; }else { return v; } }
/** * 比较其他边和当前边的权重大小 */ @Override public int compareTo(Edge o) {
int cmp;
if(this.getWeight() > o.getWeight()) { cmp=1; }else if(this.getWeight() < o.getWeight()) { cmp=-1; }else { cmp=0; }
return cmp; }
} |
三、 最小生成树定义
最小生成树用于在加权无向图中，找到成本最低的路径组成的连通子图，比如从平安金融中心出发到华润大厦，存在多条路径可达的情况下，如何找到路径最短的一条。
如下图，边的权重表示距离，从顶点0出发到达顶点4，红色边描绘的即是一棵最小生成树，它表示存在多条可到达顶点4路径的情况下，红色边集合的权重相加是最小的。
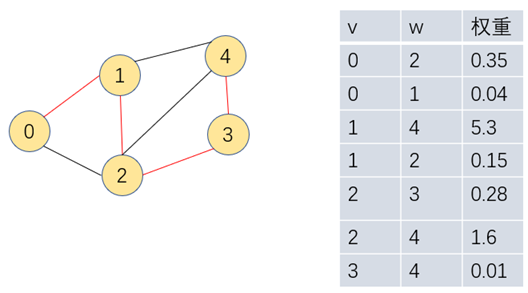
最小生成树定义：
图的生成树是一棵含有所有顶点的无环连通子图，图的最小生成树是包含所有顶点的子图中，所有边相加权重和最小的无环连通子图。
约定：因最小生成树需要包含图的所有顶点，因此只考虑连通图。
最小生成树特性：
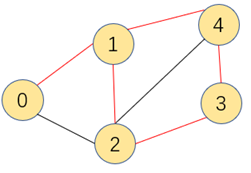
特性1：连接最小生成树中任意两个顶点会形成一个环
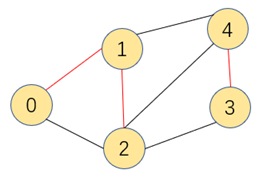
特性2：从树中删除任意一条边，会把最小生成树切割成两棵独立的子树
最小生成树的切割定理：
要找出一幅图中的最小生成树，需要通过图的切割定理完成
切割：
将一幅图按一定规则分割成两颗非空且没有交集的集合。
横切边：
连接两个属于不同集合的顶点的边称之为横切边
将上图中的最小生成树的2-3相连的边断开，则分成了如下两个（蓝色和黄色）非空无交集的集合，此时连接两个集合的2-3,2-4,1-4都是横切边。
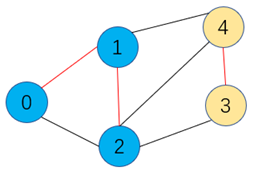
切分定理：在一副加权图中，给定任意的切分，它的横切边中的权重最小者必然属于图中的最小生成树
四、 贪心思想
贪心思想是实现最小生成树的基础思想，它的原理是通过切分定理，从一个顶点出发，使用切分定理找到最小生成树的一条边，并将改边连接的另一个顶点和边一起加到最小生成树中
再通过切分定理依次往下找到组成最小生成树的边，最终遍历完所有的N个顶点，组成了N-1条边的的最小生成树。
五、 Prim算法原理
Prim算法就是利用贪心思想实现的最小生成树，它主要把最小生成树中的顶点看成一个集合，把其他顶点看成另一个集合，每次寻找连通两个集合间的若干横切边
找到最小的横切边并加到最小生成树中，下面我们通过图示过程来了解Prim
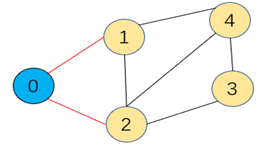
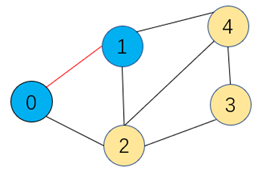
步骤1：如上无向图中，顶点0作为起点，最先加入到最小生成树中，此时顶点0为一个集合（蓝色表示），顶点1,2,3,4为另一个集合（黄色表示），连通两个集合的横切边为0-1和0-2,
通过比较0-1的权重较小，因此取0-1这条边和顶点1加入到最小生成树中
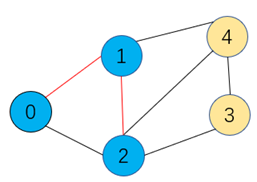
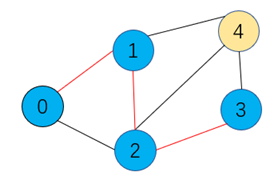
步骤2：如上无向图中，0和1作为一个最小生成树的集合，与另外的顶点2,3,4组成的集合之间的横切边是1-4,1-2,0-2，此时发现1-2的权重最小，添加到最小生成树中
此时与顶点3,4组成的集合的横切边是1-4,2-4,2-3，此时发现2-3权重最小，于是将顶点3和边2-3加入到最小生成树中，直到最后遍历完所有顶点，连通的子图即是最小生成树。
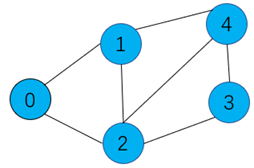
六、 Prim实现
实现Prim算法的代码前，我们再通过一次带真实权重的无向图演示来还原整个过程，我们需要声明一个最小索引优先队列，索引为顶点，值用于存放顶点与非最小生成树顶点的横切边
存在多条时取最小即可。
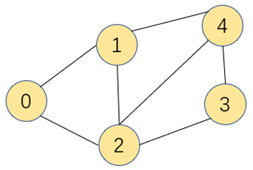
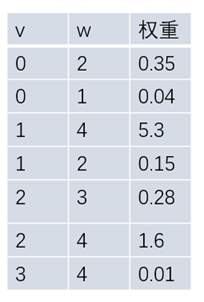
步骤一：顶点0为起点，两条横切边的权重如图，将索引优先队列顶点1和2的值更新为权重，此时取到更小的权重0.04，并从索引优先队列中弹出最小值对应的索引，即顶点1加入到最小生成树中
步骤二：0和1组成最小生成树后，更新索引优先队列，此时顶点0和1都指向顶点2，则取值更小的0.15，从横切边中取到最小的0.15权重的边1-2，再从索引优先队列中弹出最小值0.15对应的索引2
加入到最小生成树中
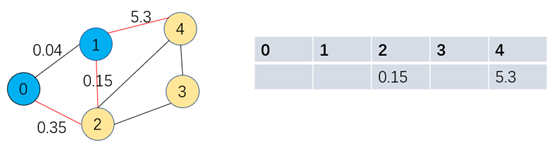
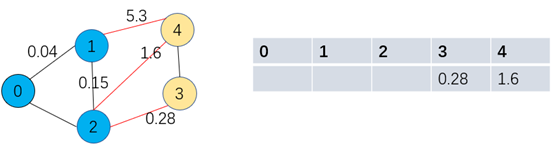
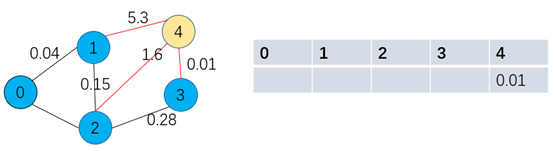
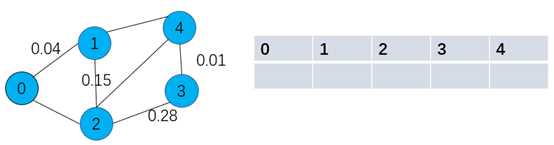
如下图演示依次类推，最后得到最小生成树
|
import com.data.struct.common.list.queue.Queue; import com.data.struct.common.tree.priority.queue.IndexMinPriorityQueue;
/** * prim算法求最小生成树 * @author jiyukai */ public class PrimMST {
// 索引存放顶点，值为顶点与最小生成树的最短横切边的权重 private Double[] edgeWeight;
// 索引存放顶点，值为顶点与最小生成树的最短横切边 private Edge[] edges;
// 存放标记顶点的数组，记录当前顶点是否在最小生成树中 private boolean[] flags;
// 存放最小生成树顶点与非最小生成树顶点的目标横切边，索引为顶点 private IndexMinPriorityQueue<Double> minQueue;
/** * 最小生成树 * @param G * @param s * @throws Exception */ public PrimMST(EdgeGraph G) throws Exception { // 索引代表顶点，初始状态下先将顶点与最小生成树的横切边设置为无穷大,并将初始顶点横切边设置为0.0 edgeWeight = new Double[G.V()]; for (int i = 0; i < G.V(); i++) { edgeWeight[i] = Double.POSITIVE_INFINITY; } edgeWeight[0] = 0.0;
edges = new Edge[G.V()]; flags = new boolean[G.V()];
// 使用最小优先队列，是为了方便从从队列中取出非最小生成树顶点到最小生成树的最短横切边 minQueue = new IndexMinPriorityQueue<Double>(G.V()+1); minQueue.insert(0, 0.0);
// 队列不为空时遍历所有顶点 while (!minQueue.isEmpty()) { visit(G, minQueue.delMin()); } }
/** * 访问顶点，逐步生成最小生成树 * @param G * @param v * @throws Exception */ private void visit(EdgeGraph G, int v) throws Exception { // 把顶点v添加到最小生成树中 flags[v] = true;
// 访问顶点的邻接边，获取每一条边 for (Edge e : G.qTable[v]) { // 访问边连接的另一个顶点w，看是否在树中，在树中跳过，不在树中，则需要比较edgeWeight[w]和v-w的大小，保留最小值 int w = e.getEither(v);
if (flags[w]) { continue; }
if (e.getWeight() < edgeWeight[w]) {
edgeWeight[w] = Double.valueOf(e.getWeight());
edges[w] = e;
if (minQueue.contains(w)) { minQueue.changeItem(w, Double.valueOf(e.getWeight())); } else { minQueue.insert(w, Double.valueOf(e.getWeight())); } } } }
/** * 获取最小生成树的所有边 * @return */ private Queue<Edge> getAllEdge() { Queue<Edge> edgeQueue = new Queue<>(); // 遍历edgeTo数组，找到每一条边，添加到队列中 for (int i = 0; i < flags.length; i++) { if (edges[i] != null) { edgeQueue.enqueue(edges[i]); } } return edgeQueue; } } |
七、 Kruskal算法原理
Kruskal算法是计算一副加权无向图的最小生成树的另外一种算法，它的主要思想是按照边的权重，从小到大进行排序，从最小值开始遍历，将最小边和边的两个顶点加入最小生成树中
已加入的边和顶点不会再加入最小生成树的边构成环，直到树中含有V-1条边为止。
步骤一：如下的无向连通图，对边和权重按从小到大排序后，首先取最小边的3-4组成一颗最小生成树
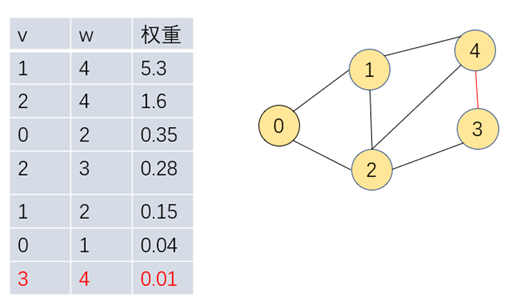
步骤二：继续遍历把0-1加入到另一颗最小生成树中
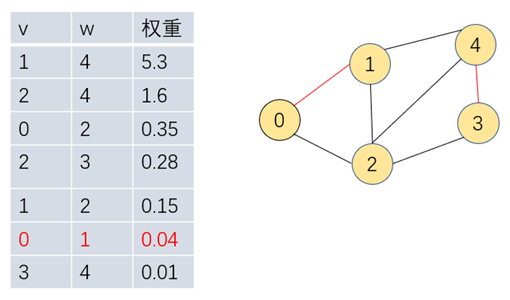
步骤三：继续遍历把1-2加入到0-1组成的最小生成树中
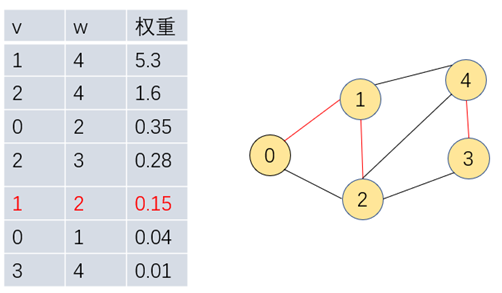
步骤四：继续遍历把2-3加入到0-1,1-2组成的最小生成树中，此时无需再往后遍历0-2,2-4,1-4，因为顶点都已在最小生成树中，树中含有V-1条边，则Kruskal计算结束，获取到一颗最小生成树
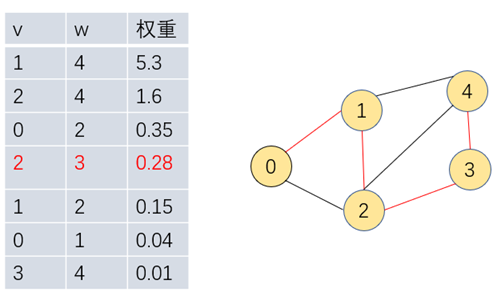
八、 Kruskal实现
|
/** * kruskal算法求最小生成树 * @author jiyukai */ public class KruskalMST {
//索引存放顶点，值为顶点与最小生成树的最短横切边 private Queue<Edge> edges;
//声明并查集，用来合并两个顶点到一棵生成树中，和判断两个顶点是否在一棵树中 private UF_Shorter_Tree usf;
//存储图中所有的边，使用最小优先队列排序，方便弹出最小值 private MinPriorityQueue<Edge> minQueue;
public KruskalMST(EdgeGraph G) { edges = new Queue<Edge>(); usf = new UF_Shorter_Tree(G.V());
//初始化最小优先队列并插入所有边，使边有序 minQueue = new MinPriorityQueue<Edge>(G.E()+1); for(Edge e : G.edges()) { minQueue.insert(e); }
while (!minQueue.isEmpty() && edges.size() < (G.V() - 1)) { //获取最小优先队列中的最小边 Edge minEdge = minQueue.delMin();
//获取边的两个顶点 int v = minEdge.getV(); int w = minEdge.getEither(v);
//如果v和w在一棵树中，则不再合并，如果不在一棵树中，则合并进最小生成树，并把边添加到最小生成树的边中 if(usf.connected(v, w)) { continue; }else { usf.union(v, w); edges.enqueue(minEdge); } } } } |
