数据结构（十）：图
一、 图概述
日常生活中使用的地图导航，每个城市看做一个顶点，城市与城市间连通的线路看做联通的边，就组成了图。除了导航，迷宫，电路板等等也是图，需要用图这种数据结构去解决很多连通问题。
二、 图的特性
图的定义：图是有一组顶点和一组能将顶点相连的边组成的数据结构
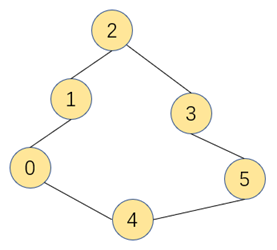
特殊的图：
平行边：连接同一对顶点的多条边
自环：一条出口和入口都来自同一个顶点的边
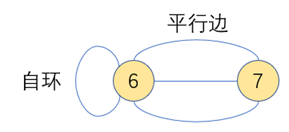
图的分类：
无向图：连接顶点的边是无方向无意义的图
有向图：连接顶点的边具有方向的图
相邻顶点：两个顶点通过一条边相连时为相邻顶点
度：顶点边的数量
子图：图所有边和相连顶点的子集
路径：A顶点到B顶点若干顺序连接的边
环：起点和终点相同，并且至少含有一条边的路径
连通图：图中每一个顶点都存在一条边到达另外一个顶点，称为连通图
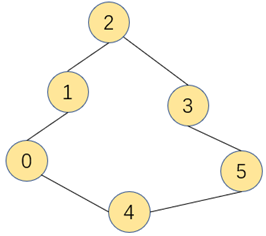
连通子图：一幅非连通图由若干连通部分组成，该连通部分称为连通子图
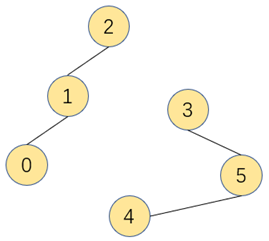
三、 图的实现
3.1 邻接矩阵
图的数据结构可以通过二维数组来表示，即邻接矩阵，如下图生成一个8*8的二维数组，通过graph[7][8]=1和graph[8][7]=1来表示顶点7和8的连通。
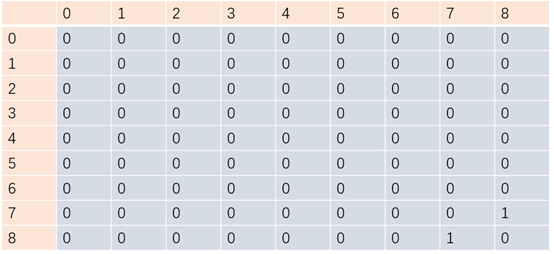
但该方式存在着内存空间使用率低的问题，N个顶点图中，得初始化N^2规模的二维数组，空间复杂度是不可接受的。
3.2 邻接表
使用一个顶点数量相同大小的数组Queue[]，索引作为图的顶点，索引对应的队列存放与顶点相连通的其他顶点，用这种方式来表示图称为邻接表。邻接表相比邻接矩阵可以大大的节省内存空间。
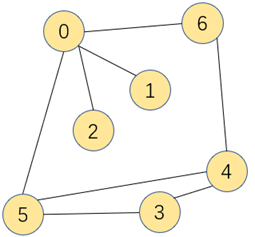
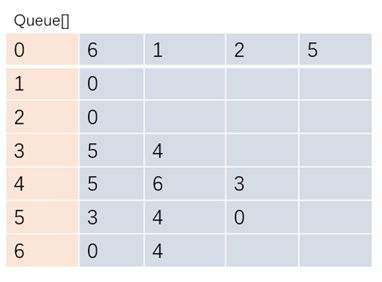
图的邻接表实现：
|
/** * 图的实现 * @author jiyukai */ public class Graph {
//定点个数 public int V;
//边的数量 public int E;
//图的邻接表 public Queue<Integer>[] qTable;
public Graph(int v) { this.V = v;
this.E = 0;
//初始化邻接表，数组中的索引为顶点，值为已队列，存放相邻的顶点 qTable = new Queue[v]; for(int i=0;i<v;i++) { qTable[i] = new Queue<Integer>(); } }
/** * 向图中添加一条边 * @param v * @param w */ public void addEdge(int v,int w) { //顶点v添加w的指向 qTable[v].enqueue(w);
//顶点w添加v的指向 qTable[w].enqueue(v);
//边加1 E++; }
/** * 返回当前顶点的数量 * @return */ public int V() { return V; }
/** * 返回当前边的数量 * @return */ public int E() { return E; }
/** * 获取与顶点V相邻的顶点 * @param V * @return */ public Queue adjoin(int V) { return qTable[V]; } } |
四、 深度优先搜索
图的搜索算法中，深度优先搜索指的是搜索到的顶点既有子结点又有兄弟结点，优先搜索子结点。如下演示为图的深度优先搜索顺序
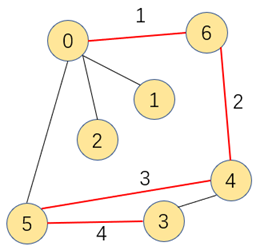
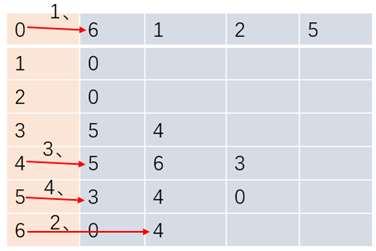
为了不对已搜索过的顶点重复搜索，我们需要有个布尔类型的数组来标记顶点是否被搜索过，搜索过的就标记为true，不再进行深度搜索，提高效率的同时，该数组也能判断顶点A到B是否相通
因为相通的代表搜索过，会被标记为true。
|
/** * 深度优先搜索 * @author jiyukai */ public class DepthSearch {
//标记顶点x是否有被搜索过 public boolean[] flags;
public int count;
/** * 深度优先搜索,找出与顶点V想通的所有顶点 * @param G * @param V */ public DepthSearch(Graph G,int V) { //长度置0 this.count = 0;
//创建一个与顶点数量相同的标记数组，标记每个顶点是否被搜索过 flags = new boolean[G.V()];
//深度优先搜索 dfs(G, V); }
/** * 深度优先搜索实现 * @param G * @param V */ public void dfs(Graph G,int V) { //被搜的顶点V标记为搜索过 flags[V] = true;
for(int w : G.qTable[V]) { if(!flags[w]) { System.out.println("搜索的顶点："+w); dfs(G, w); } }
//相通的点+1 count++; }
/** * 返回与顶点V相通的所有顶点 * @return */ public int count() { return count; }
/** * 判断顶点w是否与v相通 * @param w * @return */ public boolean isConnected(int w) { return flags[w]; }
} |
五、 广度优先搜索
图的搜索算法中，广度优先搜索指的是搜索到的顶点既有子结点又有兄弟结点，优先搜索兄弟结点。如下演示为图的广度优先搜索顺序
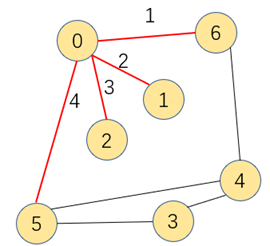
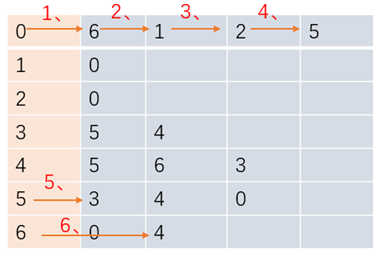
为了不对已搜索过的顶点重复搜索，我们需要有个布尔类型的数组来标记顶点是否被搜索过，搜索过的就标记为true，不再进行广度搜索，提高效率的同时，该数组也能判断顶点A到B是否相通
因为相通的代表搜索过，会被标记为true。
|
/** * 广度优先搜索 * * @author jiyukai */ public class WeightSearch {
// 标记顶点x是否有被搜索过 public boolean[] flags;
// 联通的点数量 public int count;
// 用来存储待搜索邻接表的点 private Queue<Integer> waitSearch;
/** * 深度优先搜索,找出与顶点V想通的所有顶点 * * @param G * @param V */ public WeightSearch(Graph G, int V) { // 长度置0 this.count = 0;
// 创建一个与顶点数量相同的标记数组，标记每个顶点是否被搜索过 flags = new boolean[G.V()];
// 初始化待搜索顶点队列 waitSearch = new Queue<>();
// 深度优先搜索 wfs(G, V); }
/** * 深度优先搜索实现 * * @param G * @param V */ public void wfs(Graph G, int V) { // 被搜的顶点V标记为搜索过 flags[V] = true;
// 将待搜索的元素入队列 for (int w : G.qTable[V]) { waitSearch.enqueue(w); }
while (!waitSearch.isEmpty()) { int searchKey = waitSearch.dequeue(); if (!flags[searchKey]) { wfs(G, searchKey); } }
// 相通的点+1 count++; }
/** * 返回与顶点V相通的所有顶点 * * @return */ public int count() { return count; }
/** * 判断顶点w是否与v相通 * * @param w * @return */ public boolean isConnected(int w) { return flags[w]; }
} |
六、 路径查找
导航中常用的一个场景就是起点s到重点v之间是否存在一条可连通的路径，若存在，需要走什么样的路到达。
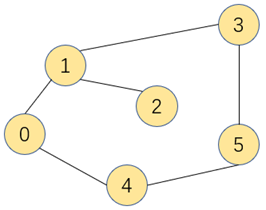
基于深度搜索来实现图的搜索，新增一个数组conn[]来记录各个连通点之间的关系，索引为顶点，值为指向顶点的相邻顶点，假设0为起点，在conn数组构建完毕后，我们通过索引0找到顶点4
在通过索引4找到顶点5，依次找下去，并将找到的顶点依次入栈，则最后能找到和0相通的其他顶点和中间经过的路径。
将找到的顶点依次入栈
|
/** * 基于深度优先搜索实现的路径查找 * @author jiyukai */ public class DepthSearchPath {
// 标记顶点x是否有被搜索过 public boolean[] flags;
// 联通的点数量 public int count;
// 初始化起点 public int s;
// 连通顶点的关系 public int conn[];
/** * 深度优先搜索,找出与顶点V想通的所有顶点 * @param G * @param V */ public DepthSearchPath(Graph G, int s) { // 长度置0 this.count = 0;
// 创建一个与顶点数量相同的标记数组，标记每个顶点是否被搜索过 flags = new boolean[G.V()];
// 初始化连通顶点的关系数组 conn = new int[G.V()];
// 初始化起点 this.s = s;
// 深度优先搜索 wfs(G, s); }
/** * 深度优先搜索实现 * @param G * @param V */ public void wfs(Graph G, int v) { // 被搜的顶点V标记为搜索过 flags[v] = true;
for (int w : G.qTable[v]) { if (!flags[w]) { conn[w] = v; wfs(G, w); } }
// 相通的点+1 count++; }
/** * 返回与顶点V相通的所有顶点 * @return */ public int count() { return count; }
/** * 判断顶点w是否与v相通 * @param w * @return */ public boolean isConnected(int w) { return flags[w]; }
/** * 找出s到顶点v的路径 * @param v * @return */ public Stack<Integer> pathTo(int v){
//判断是否连接 if(!isConnected(v)) { return null; }
//创建存放连通图的栈 Stack<Integer> stack = new Stack<Integer>();
//找出与起点s连通路径上的顶点 for(int x=v;x!=s;x=conn[x]) { stack.push(x); }
//起点入栈 stack.push(s);
return stack; } } |
