数据结构（一）：算法分析
一、 数据结构与算法概述
1.1数据结构
数据结构是一门研究程序设计中的对象，以及他们的关系及操作的学科，说白了就是把各种数据元素按照一定的关系组织成集合，用来对其组织，存储和操作
1.2算法
算法即解决程序设计问题的方案，通过一定规范的输入，在一定时间内获得需求的输出结果
1.3程序
程序=数据结构+算法
二、 数据结构分类
2.1逻辑结构
逻辑结构是把数据元素集合的抽象模型，常见的有集合，线性结构，树形结构和图形结构
集合：若干数据元素属于同一个集合，再无其他关系
线性结构：数据元素之间有一一对应的关系
树形结构：数据元素之间有一对多的关系
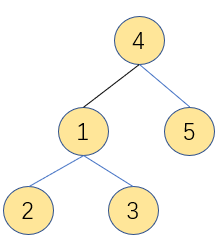
图形结构：数据元素之间有多对多的关系
2.2物理结构
物理结构是逻辑结构在计算机中的表示方式，一般有顺序存储结构和链式存储结构
顺序存储结构：
把若干数据元素存储到地址连续的数据单元里的结构，常用的数组就是这种结构，顺序存储结构对于指定元素的查找很方便，就像书的目录一般，通过指定位置即可找到对应的值，但也存在一定弊端
由于结构是连续的，对于新插入或剔除的数据，就得需要整个结构重排，因此有了链式存储结构。
链式存储结构：
数据元素存储在不连续的存储单元中，通过元素中引入指针指向其他数据元素的地址，来找到互相关联的数据。
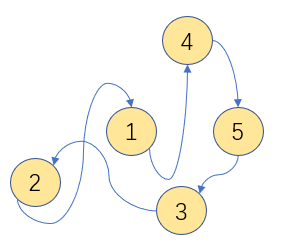
三、 算法的优化考量
算法在计算中的运行是需要时间和内存空间的，对算法优化的考量，要么牺牲时间换空间，要么牺牲空间换时间，没有时间和空间同时能优化到极致的算法。
从广东去北京，坐飞机时间快，但费用高，步行的话费用低但时间长，算法的优化也是如此，我们可以用不同的算法，用不同的成本去解决问题，见如下示例：
计算1到100的和
这个数学问题可以用如下三种方式解决，
第一种是1到100的每个数都相加一次，在for循环中执行了100次相加计算
第二种是使用高斯公式直接求和，只进行了一次公式计算
第三种是使用递归的方式求和，每次递归，都要执行一次方法，这样100的求和需要在内存空间中开辟100个栈内存
综上，第二种的时间比第一种少，一二种算法比第三种算法节省空间，所以选取算法二最佳
四、 算法时间复杂度分析
4.1影响算法时间的因素
三种因素会影响到算法的时间，分别是算法采用的策略，问题输入的规模和计算机硬件的质量，实际计算程序的时间复杂度时，我们并不关心是用哪种语言编写，并且计算机的硬件资源也不可控
那么在算法固定的情况下，我们通过改变问题输入的规模来验证算法时间复杂度的规律。
4.2函数渐进增长
上述问题的前两种解法，计算机进行计算的次数如下，第一种合计做了2n+3次计算，第二种合计做了3次计算，那么不同次数的计算，对于算法的影响程度有多大？
实验4.2.1
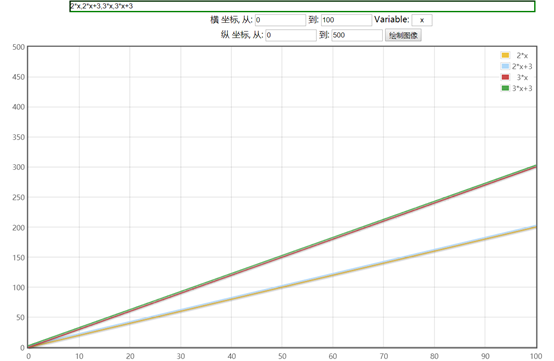
假设有四组程序，通过函数在坐标图上的表现(横坐标输入规模，纵坐标算法耗时)如下图
- 算法A1的执行次数为2n
- 算法A2的执行次数为2n+3
- 算法B1的执行次数为3n
- 算法B2的执行次数为3n+3
通过函数的直线可看出，随着n的逐渐增大，算法A1,A2逐渐重叠，算法B1,B2也逐渐重叠，因此我们可得出结论：
随着输入规模的增大，算法的常熟操作可以忽略不计
实验4.2.2
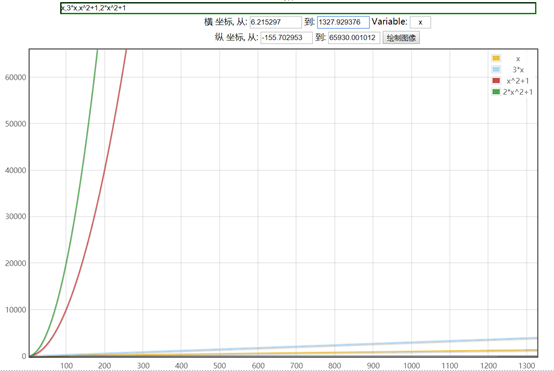
假设有四组程序，通过函数在坐标图上的表现(横坐标输入规模，纵坐标算法耗时)如下图
- 算法A1的执行次数为n
- 算法A2的执行次数为3n
- 算法B1的执行次数为n^2+1
- 算法B2的执行次数为2n^2+1
通过函数的直线可看出，随着n的逐渐增大，算法A1,A2逐渐重叠，算法B1,B2也逐渐重叠，因此我们可得出结论：
随着输入规模的增大，与最高次项相乘的常数可以忽略
实验4.2.3
假设有四组程序，通过函数在坐标图上的表现(横坐标输入规模，纵坐标算法耗时)如下图
- 算法A1的执行次数为n^2
- 算法A2的执行次数为2n^2+2n
- 算法B1的执行次数为n^3
- 算法B2的执行次数为2n^3+2n
通过函数的直线可看出，随着n的逐渐增大，A1的算法要明显优于B1，A2的算法也明显优于B2，因此我们可得出结论：
随着输入规模的增大，最高此项的指数不可忽略，并且随着指数的增长，算法耗时愈发明显增加
实验4.2.4
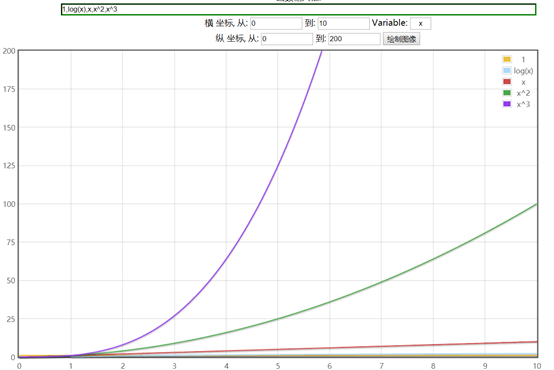
假设有四组程序，通过函数在坐标图上的表现(横坐标输入规模，纵坐标算法耗时)如下图
- 算法A1的执行次数为1
- 算法A2的执行次数为log(n)
- 算法A3的执行次数为n
- 算法A4的执行次数为n^2
- 算法A5的执行次数为n^3
通过函数的直线可看出，随着n的逐渐增大，最高次项指数高的，耗时增加愈发的高，因此我们可得出结论：
算法函数中n的最高次幂越小，算法效率更高
4.3影响算法的规律总结
- 随着输入规模的增大，算法的常熟操作可以忽略不计
- 随着输入规模的增大，与最高次项相乘的常数可以忽略
- 随着输入规模的增大，最高此项的指数不可忽略，并且随着指数的增长，算法耗时愈发明显增加
- 算法函数中n的最高次幂越小，算法效率更高
五、 算法时间复杂度记法
5.1大O记法
计算算法复杂度时，算法的总执行次数T(n)决定了算法执行时间的增长率O(f(n))，用大写O()来体现算法时间复杂度的记法，我们称之为大O记法。一般情况下，随着输入规模n的增大
T(n)增长最慢的算法为最优算法。
- 由于随着输入规模的增大，算法的常熟操作可以忽略不计，所以执行次数只保留最高阶，若为常数，我们用1来代替，
- 由于随着输入规模的增大，与最高次项相乘的常数可以忽略，所以执行次数保留最高阶，并去除与该高阶相乘的常数
综上，如下算法对应的大O计法可表示如下：
算法一执行次数为1——O（1）
算法二执行次数为n+3——O（n）
算法三执行次数为2n^2+3——O（n^2）
5.2常见的大O阶
5.2.2线性阶
线性阶就是随着输入规模的扩大，对应计算次数呈直线增长，如下算法循环体中的代码需要执行n次，故大O计法为O（n）
5.2.3平方阶
如下算法循环体中的外层的i循环需要执行n次，里层的j循环需要执行n次，故大O计法为O（n^2）
5.2.4立方阶
如下算法循环体中的外层的i循环需要执行n次，里层的j循环需要执行n次，最里层的k循环需要执行n次，故大O计法为O（n^3）
5.2.5对数阶
对数函数log(n)也可以表示为log2(n)，该函数的大O计法为O（logn）
5.2.6常数阶
一般不涉及循环操作的都是常数阶，因为它不会随着n的增长而增加操作次数, 由于随着输入规模的增大，算法的常熟操作可以忽略不计，所以执行次数只保留最高阶，若为常数，我们用1来代替
故该函数的大O计法为O（1）
5.2.7各大O阶的复杂程度对比如下
综上及结合如下函数图像可得，各种类型的大O阶复杂程度如下
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)
5.2最坏情况
最坏情况是一种保证，在应用中，这是一种最基本的保障，即使在最坏情况下，也能够正常提供服务，所以，除非特别指定，我们提到的运行时间都指的是最坏情况下的运行时间
六、 算法空间复杂度分析
现代的计算机设备内存都比较大，基本都是4G起步，优秀一点的32G也遍地皆是，加上JVM有自己的内存优化机制如及时编译，垃圾回收等，所以内存正常情况下使用一般不会有大问题
但是对于空间复杂度的评估，还是要懂的。
6.1内存计算公式
对象占用内存 = 对象头开销 + 实例数据(如果是引用类型则包括 变量 和 实例 两部分开销) + 填充数据。
a.对象头开销
指向类引用、垃圾收集信息、同步信息等。
32位JVM 对象头8字节，数组对象头16字节。
64位JVM 对象头16字节，数组对象头24字节，空对象 / 空数组 都只有对象头。
注：对象头要用来存储对象自身的运行时数据，如hashcode、gc分代年龄
b.实例数据
基本类型在内存只有值所占用空间大小。
引用类型包含 变量 和 值 两部分占用空间大小(引用变量就相当于指针，用一个系统存储单元存储。值则是堆中实例的大小)。
c.填充数据
hotspot JVM里，对象占用空间是8字节对齐的。因为在内存中一个存储单元是8字节的。
意思是一个Java对象使用的内存一定是8字节的整数倍，如果通过计算后发现对象所需内存不是8字节的整数倍，则会将其填充为8字节的倍数。
例如：对象实例可能需要内存为30字节或者28字节等，都会被填充为32字节。
d.继承关系(不计算父类对象头开销)
子类对象占用内存 = 子类对象头开销 + 子类实例数据 + (父类实例数据+填充数据) + 填充数据。
示例1：
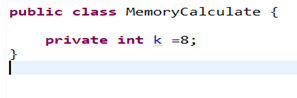
上述代码类对象头开销16字节+int类型的k占用4字节，相加为20字节，因为64位机器对象所需内存为8字节的整数倍，故被自动填充为24字节，如下为Java中常见数据类型的内存字节占用一览。
示例2：
若是新实例化了一个数组对象temp，则需要新增占用数组对象头24字节，50*2（char字节占用）=100字节，即该数组占用总空间为124字节，被自动填充到128字节
故该段代码的总字节占用为128+24=152字节
6.2 Java中常见数据类型的内存字节占用
|
数据类型 |
内存占用字节数 |
|
byte |
1 |
|
short |
2 |
|
int |
4 |
|
long |
8 |
|
float |
4 |
|
double |
8 |
|
boolean |
1 |
|
char |
2 |
