[编程题] lk [股票类买卖问题(多个情况)--动态规划问题的综合提升]
[编程题] lk [股票类买卖问题(多个情况)--动态规划问题的综合提升]
题目:lk:121 122 123 188 309 714 LeetCode 上拿下如下题目:
买卖股票的最佳时机
买卖股票的最佳时机 II
买卖股票的最佳时机 III
买卖股票的最佳时机 IV
最佳买卖股票时机含冷冻期
买卖股票的最佳时机含手续费
一、股票类动态规划问题探究
本类动态规划的核心点记录
① 状态定义
我们涉及到天数,涉及到最大的交易次数,涉及到是否今天是买入还是卖出;故需要三维的dp数组才能很好的解决此问题。
这个问题的「状态」有三个,第一个是第i天获得的利润(0~i-1),第二个是允许交易的最大次数(1~k),第三个是当前的持有状态(0:未持有,1:持有)
//注意默认大小要生成n,k+1的大小的。都是n能取到n-1是最后一个数组索引和k值表示买卖次数,能取到k索引
int[][][] dp = new int[n][k+1][2];
② 初始条件
含义
dp[-1][k][0] = 0
解释:因为 i 是从 0 开始的,所以 i = -1 意味着还没有开始,这时候的利润当然是 0 。
dp[-1][k][1] = -infinity
解释:还没开始的时候,是不可能持有股票的,用负无穷表示这种不可能。
dp[i][0][0] = 0
解释:因为 k 是从 1 开始的,所以 k = 0 意味着根本不允许交易,这时候利润当然是 0 。
dp[i][0][1] = -infinity
解释:不允许交易的情况下,是不可能持有股票的,用负无穷表示这种不可能。
总结一下初始条件:
//当第0天的话
if(i==0){
//没持股,肯定利润为0
dp[i][j][0] = 0;
//持有股,那么肯定是买了第一股,利润为负
dp[i][j][1] = -prices[0];
}else{
...
}
③ 状态转移方程
本人经过在第一次思考的时候,主要发现问题在于交易次数j的定义问题这里有不同的思路:
写法1:题目规定完整交易最多2次(买和卖算1次),那么定义 j=2
/*特别注意:这里在dp[i][j][0]中的参数2(dp[i-1][j][1]+prices[i] )为什么不是dp[i-1][j-1][1]+prices[i],是因为我们把k值跟买关联,只要一买进,就代表着k值+1交易一次了,(即昨天买进一股,代表着新一轮交易开始啦)也代表着上一轮的完整交易结束,如果在买的时候j就变化,卖的时候j也变化,那么,买和卖这么一次,j已经达到2了,停止交易了,而题目给的是两次完整的交易,如果偏要买卖都把j变化的话,初始化值j的时候必须设置为4(本题而言)*/
dp[i][j][0] = Math.max(dp[i-1][j][0], dp[i-1][j][1]+prices[i]); //第i天手里没有持有股
dp[i][j][1] = Math.max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]); //第i天手里持有股
即:j就设置为题目给定的买卖数。交易两次,把k和买入做关联,只要是前一天买入了,那么后一天的买卖数就加1;而前一天卖出的话,还没买,交易数不变。
特点:时间复杂度小,即买卖2次,j也就只在买入的2次里发生了变化 (time:6ms)
写法1:题目规定完整交易最多2次(买和卖算1次),那么定义 j=2*交易次数=4
//解释:j设置为买卖交易的次数的2倍,即交易两次,j设置为4;前一天买入 j就增加,前一天卖出,j也增加。总共两次买卖4次操作,j变化4
dp[i][j][0] = Math.max(dp[i-1][j][0], dp[i-1][j-1][1]+prices[i]); //第i天手里没有持有股
dp[i][j][1] = Math.max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]); //第i天手里持有股
即:交易两次,指定k=2*2 (原因是在状态方程中买一次加j变化1,卖一次也j变化1。故买卖两次,即j变化4次)
特点:白白的增加了2倍的时间复杂度,多了很多操作。 (time:10ms))
④ 返回值
我们返回第n天的手里没有出游股的最大交易次数时候的利润值即可,如下:
return dp[n-1][k][0];
⑤ 上述以最多2次交易的题目案例为例,代码参考如下
<1>使用上述的写法1写的代码:
好理解,时间复杂度大,循环次数多
//方法1:指定k = 买卖数*2
//交易两次,指定k=2*2 (原因是在状态方程中买一次加j变化1,卖一次也j变化1。故买卖两次,即j变化4次)
//特点:白白的增加了2倍的时间复杂度,多了很多操作。 (time:10ms))
public int maxProfit1(int[] prices) {
if(prices.length<=1){return 0;}
int n = prices.length;
int k = 2*2;
//new int[n][k][2]; 参数1:是第i天为止的利润,参数2:表示最多可以完成几笔交易,参数3:0表示未持有股票,1表示持有股票
int[][][] dp = new int[n][k+1][2];
for(int i=0;i<n;i++){
for(int j=1;j<=k;j++){
if(i==0){
dp[i][j][0] = 0;
dp[i][j][1] = -prices[0];
}else{
//解释:j设置为买卖交易的次数的2倍,即交易两次,j设置为4;前一天买入 j就增加,前一天卖出,j也增加。总共两次买卖4次操作,j变化4
dp[i][j][0] = Math.max(dp[i-1][j][0], dp[i-1][j-1][1]+prices[i]); //第i天手里没有持有股
dp[i][j][1] = Math.max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]); //第i天手里持有股
}
}
}
//我们返回第n天的手里没有出游股的最大交易次数时候的利润值即可,如下:
return dp[n-1][k][0];
}
输出:时间复杂度高
<1>使用上述的写法2写的代码:
时间复杂度小,循环次数少
//方法2:指定k = 买卖数
//交易两次,把k和买入做关联,只要是前一天买入了,那么后一天的买卖数就加1;而前一天卖出的话,还没买,交易数不变。
//特点:时间复杂度小,即买卖2次,j也就只在买入的2次里发生了变化 (time:6ms)
public int maxProfit1(int[] prices) {
if(prices.length<=1){return 0;}
int n = prices.length;
int k = 2;
//new int[n][k][2]; 参数1:是第i天为止的利润,参数2:表示最多可以完成几笔交易,参数3:0表示未持有股票,1表示持有股票
int[][][] dp = new int[n][k+1][2];
for(int i=0;i<n;i++){
for(int j=1;j<=k;j++){
if(i==0){
dp[i][j][0] = 0;
dp[i][j][1] = -prices[0];
}else{
/*特别注意:这里在dp[i][j][0]中的参数2(dp[i-1][j][1]+prices[i] )为什么不是dp[i-1][j-1][1]+prices[i],
是因为我们把k值跟买关联,只要一买进,就代表着k值+1交易一次了,(即今天昨天买进一股,代表着新一轮交易开始啦)
也代表着上一轮的完整交易结束,如果在买的时候j就变化,卖的时候j也变化,那么,买和卖这么一次,j已经达到2了,停止
交易了,而题目给的是两次完整的交易,如果偏要买卖都把j变化的话,初始化值j的时候必须设置为4(本题而言)*/
dp[i][j][0] = Math.max(dp[i-1][j][0], dp[i-1][j][1]+prices[i]); //第i天手里没有持有股
dp[i][j][1] = Math.max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]); //第i天手里持有股
}
}
}
//我们返回第n天的手里没有出游股的最大交易次数时候的利润值即可,如下:
return dp[n-1][k][0];
}
输出:

至此,状态的定义、初始值情况、状态转移方程都定义好了,即可以完成如下的多种情况的练习了,都套用上述模板。
二、[其他各种情况的题目练习]
题目1 股票买卖一次买入一次卖出
121. 买卖股票的最佳时机(力扣)
方法:一次遍历记录最低价格和最大利润
输入输出

方法1:一次遍历同时记录最小值和最大利润
class Solution {
//方法:一次遍历记录最低价格和最大利润
public int maxProfit(int[] prices) {
int minPrice = Integer.MAX_VALUE;
int maxprofits = 0;
for(int i=0;i<prices.length;i++){
if(prices[i] < minPrice){
minPrice = prices[i];
}
maxprofits = (prices[i]-minPrice) > maxprofits?(prices[i]-minPrice):maxprofits;
}
return maxprofits;
}
}
输出:

方法2:套用该类题的动态规划模板
//方法2:动态规划套模板
public static int maxProfit2(int[] prices) {
if(prices.length<=1){return 0;}
int n = prices.length;
int k = 1;
//new int[n][k][2]; 参数1:是第i天为止的利润,参数2:表示最多可以完成几笔交易,参数3:0表示未持有股票,1表示持有股票
int[][][] dp = new int[n][k+1][2];
for(int i=0;i<n;i++){
for(int j=1;j<=k;j++){
if(i==0){
dp[i][j][0] = 0;
dp[i][j][1] = -prices[0];
}else{
/*特别注意:这里在dp[i][j][0]中的参数2(dp[i-1][j][1]+prices[i] )为什么不是dp[i-1][j-1][1]+prices[i],是因为我们把k值跟买关联,只要一买进,就代表着k值+1交易一次了,(即今天昨天买进一股,代表着新一轮交易开始啦)也代表着上一轮的完整交易结束,如果在买的时候j就变化,卖的时候j也变化,那么,买和卖这么一次,j已经达到2了,停止交易了,而题目给的是两次完整的交易,如果偏要买卖都把j变化的话,初始化值j的时候必须设置为4(本题而言)*/
dp[i][j][0] = Math.max(dp[i-1][j][0], dp[i-1][j][1]+prices[i]); //第i天手里没有持有股
dp[i][j][1] = Math.max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]); //第i天手里持有股
}
}
}
//我们返回第n天的手里没有出游股的最大交易次数时候的利润值即可,如下:
return dp[n-1][k][0];
}
方法3:动态规划:因为是一次交易,把上述的数组缩减为2维
//方法3:动态规划:因为是一次交易,把上述的数组缩减为2维
public static int maxProfit(int[] arr){
if(arr.length<=1){return 0;}
//因为只能买卖一次,所以我们可以用二维表示
int n = arr.length;
int[][] dp = new int[n][2];
for(int i=0;i<n;i++){
if(i==0){
dp[i][0] = 0; //未持有
dp[i][1] = -arr[i]; //第一笔买入,利润为负
}else{
//动态转移方程
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+arr[i]); //参数2 是前一天卖出
//dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-arr[i]); //参数2:买入; 参数2这么写不对
dp[i][1] = Math.max(dp[i-1][1],0-arr[i]); //因为只有一次交易,前一次没买入,那么这次买入的话利润就是-arr[i]
}
}
//返回
return dp[n-1][0];
}
题目2 股票买卖2次买入2次卖出
123. 买卖股票的最佳时机 III
题目
输入输出

方法1:动态规划
写法1:j=买卖次数*2
//方法1:指定k = 买卖数*2
//交易两次,指定k=2*2 (原因是在状态方程中买一次加j变化1,卖一次也j变化1。故买卖两次,即j变化4次)
//特点:白白的增加了2倍的时间复杂度,多了很多操作。 (time:10ms))
public int maxProfit1(int[] prices) {
if(prices.length<=1){return 0;}
int n = prices.length;
int k = 2*2;
//new int[n][k][2]; 参数1:是第i天为止的利润,参数2:表示最多可以完成几笔交易,参数3:0表示未持有股票,1表示持有股票
int[][][] dp = new int[n][k+1][2];
for(int i=0;i<n;i++){
for(int j=1;j<=k;j++){
if(i==0){
dp[i][j][0] = 0;
dp[i][j][1] = -prices[0];
}else{
//解释:j设置为买卖交易的次数的2倍,即交易两次,j设置为4;前一天买入 j就增加,前一天卖出,j也增加。总共两次买卖4次操作,j变化4
dp[i][j][0] = Math.max(dp[i-1][j][0], dp[i-1][j-1][1]+prices[i]); //第i天手里没有持有股
dp[i][j][1] = Math.max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]); //第i天手里持有股
}
}
}
//我们返回第n天的手里没有出游股的最大交易次数时候的利润值即可,如下:
return dp[n-1][k][0];
}
动态规划
写法2:j=买卖次数=2
//方法2:指定k = 买卖数
//交易两次,把k和买入做关联,只要是前一天买入了,那么后一天的买卖数就加1;而前一天卖出的话,还没买,交易数不变。
//特点:时间复杂度小,即买卖2次,j也就只在买入的2次里发生了变化 (time:6ms)
public int maxProfit(int[] prices) {
if(prices.length<=1){return 0;}
int n = prices.length;
int k = 2;
//new int[n][k][2]; 参数1:是第i天为止的利润,参数2:表示最多可以完成几笔交易,参数3:0表示未持有股票,1表示持有股票
int[][][] dp = new int[n][k+1][2];
for(int i=0;i<n;i++){
for(int j=1;j<=k;j++){
if(i==0){
dp[i][j][0] = 0;
dp[i][j][1] = -prices[0];
}else{
/*特别注意:这里在dp[i][j][0]中的参数2(dp[i-1][j][1]+prices[i] )为什么不是dp[i-1][j-1][1]+prices[i],
是因为我们把k值跟买关联,只要一买进,就代表着k值+1交易一次了,(即今天昨天买进一股,代表着新一轮交易开始啦)
也代表着上一轮的完整交易结束,如果在买的时候j就变化,卖的时候j也变化,那么,买和卖这么一次,j已经达到2了,停止
交易了,而题目给的是两次完整的交易,如果偏要买卖都把j变化的话,初始化值j的时候必须设置为4(本题而言)*/
dp[i][j][0] = Math.max(dp[i-1][j][0], dp[i-1][j][1]+prices[i]); //第i天手里没有持有股
dp[i][j][1] = Math.max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]); //第i天手里持有股
}
}
}
//我们返回第n天的手里没有出游股的最大交易次数时候的利润值即可,如下:
return dp[n-1][k][0];
}
题目3 股票买卖多次买入多次卖出
122. 买卖股票的最佳时机 II
题目:
输入输出:

方法1:贪心算法解决
当我们在今天想买入的时候不仿先看看明天的时候能不能卖出(即明天比今天高,可获利);每次考虑局部最优
class Solution {
//方法1:贪心:当我们在今天想买入的时候不仿先看看明天的时候能不能卖出(即明天比今天高,可获利);每次考虑局部最优
// 贪心思想(每天都看后一天的情况,如果后一天价格高,就选择今天买入)
public int maxProfit(int[] prices) {
int money = 0;
for(int i=0;i<prices.length-1;i++){ //为了保证数组不越界,i指向倒数第2个数就知道自己要不要最后买入了,不满入就退出循环结束了
if(prices[i+1]>prices[i]){
money += prices[i+1]-prices[i]; //如果后一天比前一天的值大,前一天就买入,后一天卖出
}
}
return money;
}
}
输出:
方法2:动态规划
思想参考:
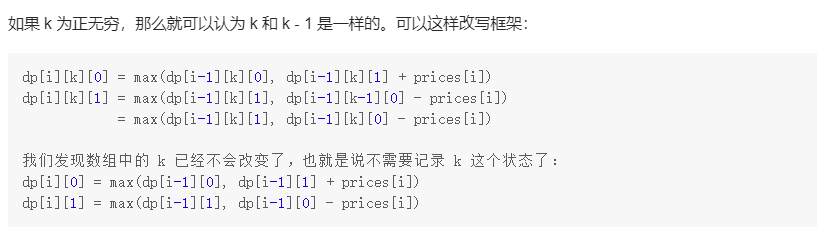
代码
//方法2:动态规划:因为是多次交易,k已经无需记录了。把上述的数组缩减为2维
public static int maxProfit(int[] arr){
if(arr.length<=1){return 0;}
//因为只能买卖一次,所以我们可以用二维表示
int n = arr.length;
int[][] dp = new int[n][2];
for(int i=0;i<n;i++){
if(i==0){
dp[i][0] = 0; //未持有
dp[i][1] = -arr[i]; //第一笔买入,利润为负
}else{
//动态转移方程
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+arr[i]); //参数2 是前一天卖出
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-arr[i]); //因为多次交易,前一次没买入,则这次,dp[i-1][0]-arr[i]
}
}
//返回
return dp[n-1][0];
}
题目3股票买卖K次买进卖出
188. 买卖股票的最佳时机 IV
题目
输入输出

直接套公式存在的问题:

代码
class Solution {
//方法1:动态规划
public int maxProfit(int k, int[] prices) {
if(prices.length<=1){return 0;}
if(k>prices.length/2){
return maxProfit_k(prices);
}
int n = prices.length;
//int k; //直接使用形参k
//new int[n][k][2]; 参数1:是第i天为止的利润,参数2:表示最多可以完成几笔交易,参数3:0表示未持有股票,1表示持有股票
int[][][] dp = new int[n][k+1][2];
for(int i=0;i<n;i++){
for(int j=1;j<=k;j++){
if(i==0){
dp[i][j][0] = 0;
dp[i][j][1] = -prices[0];
}else{
/*特别注意:这里在dp[i][j][0]中的参数2(dp[i-1][j][1]+prices[i] )为什么不是dp[i-1][j-1][1]+prices[i],
是因为我们把k值跟买关联,只要一买进,就代表着k值+1交易一次了,(即今天昨天买进一股,代表着新一轮交易开始啦)
也代表着上一轮的完整交易结束,如果在买的时候j就变化,卖的时候j也变化,那么,买和卖这么一次,j已经达到2了,停止
交易了,而题目给的是两次完整的交易,如果偏要买卖都把j变化的话,初始化值j的时候必须设置为4(本题而言)*/
dp[i][j][0] = Math.max(dp[i-1][j][0], dp[i-1][j][1]+prices[i]); //第i天手里没有持有股
dp[i][j][1] = Math.max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i]); //第i天手里持有股
}
}
}
//我们返回第n天的手里没有出游股的最大交易次数时候的利润值即可,如下:
return dp[n-1][k][0];
}
//方法:可以买卖多次的情况,调用贪心解决无线次买卖问题
/*思想:当我们在今天想买入的时候不仿先看看明天的时候能不能卖出(即明天比今天高,可获利);每次考虑局部最优
贪心思想(每天都看后一天的情况,如果后一天价格高,就选择今天买入)*/
public int maxProfit_k(int[] prices) {
if(prices.length==0) {return 0;}
int money = 0;
for(int i=0;i<prices.length-1;i++){ //为了保证数组不越界,i指向倒数第2个数就知道自己要不要最后买入了,不满入就退出循环结束了
if(prices[i+1]>prices[i]){
money += prices[i+1]-prices[i]; //如果后一天比前一天的值大,前一天就买入,后一天卖出
}
}
return money;
}
}
输出:

题目4 股票买卖K次买进卖出含义冷冻期
309. 最佳买卖股票时机含冷冻期
题目
思想:
主要点:

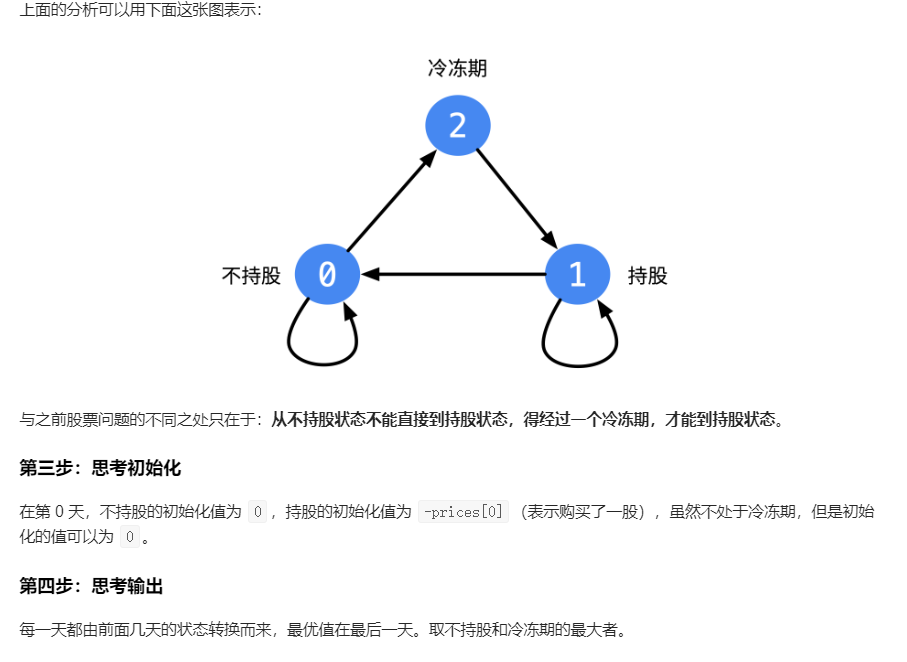
代码思路
class Solution {
//动态规划:把状态改为3: 0 表示不持股;1 表示持股; 2 表示处在冷冻
public int maxProfit(int[] prices) {
if(prices.length<=1){return 0;}
//因为只能买卖一次,所以我们可以用二维表示
int n = prices.length;
int[][] dp = new int[n][3];
for(int i=0;i<n;i++){
if(i==0){
dp[i][0] = 0; //未持有
dp[i][1] = -prices[i]; //第一笔买入,利润为负
dp[i][2] = 0; //不可能事件,第0天就冻结
}else{
//动态转移方程
//dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]); //参数2 是前一天卖出
//因为有冷冻期,所以在买入的时候要从其i-2天状态看
//dp[i][1] = Math.max(dp[i-1][1],dp[i-2][0]-prices[i]); //买入
//0 表示不持股;1 表示持股; 2 表示处在冷冻
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][2] - prices[i]);
dp[i][2] = dp[i - 1][0]; //冷冻期必须从不持股来,因为刚刚卖了
}
}
//返回
return Math.max(dp[n-1][0],dp[n-1][2]);
}
}
输出:

题目4 股票买卖K次买进卖出有手续费
714. 买卖股票的最佳时机含手续费
题目:

思路:
我们只要把可以买卖k次的情况在卖出的时候交个手续费就可以了,买入的时候不用交手续费,如下
//动态转移方程
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]-fee);//参数2是前一天卖出,但是要收手续费
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-prices[i]); //前一天买入,买入是可以不收手续费的
Java代码
class Solution {
//动态规划
public int maxProfit(int[] prices, int fee) {
if(prices.length<=1){return 0;}
//因为只能买卖一次,所以我们可以用二维表示
int n = prices.length;
int[][] dp = new int[n][2];
for(int i=0;i<n;i++){
if(i==0){
dp[i][0] = 0; //未持有
dp[i][1] = -prices[i]; //第一笔买入,利润为负
}else{
//动态转移方程
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]-fee); //参数2 是前一天卖出,但是要收手续费
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-prices[i]); //前一天买入,买入是可以不收手续费的
}
}
//返回
return dp[n-1][0];
}
}



