数独棋盘生成器
Github链接
作业链接
项目要求
项目需求
利用程序随机构造出N个已解答的数独棋盘 。
输入
数独棋盘题目个数N(0<N<=1000000)
输出
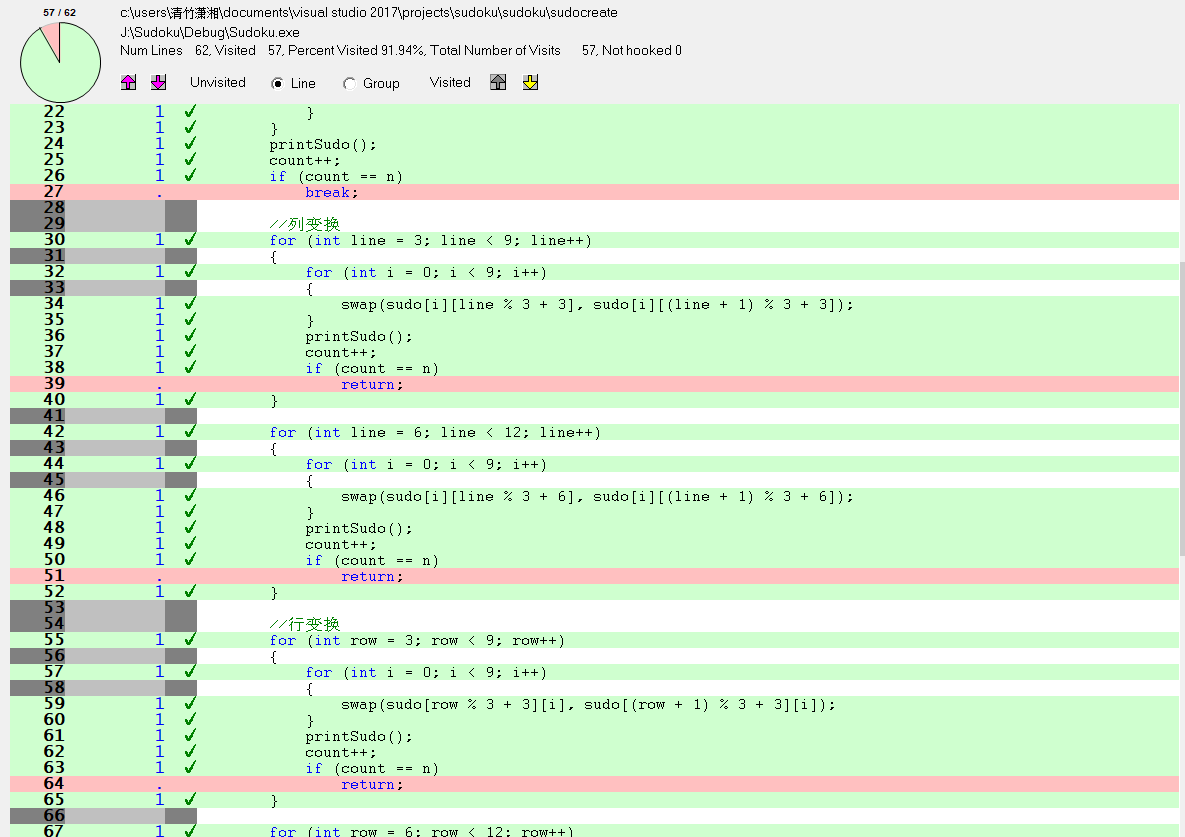
随机生成N个不重复的已解答完毕的数独棋盘,并输出到sudoku.txt中,输出格式见下输出示例。
[2017.9.4 新增要求] 在生成数独矩阵时,左上角的第一个数为:(学号后两位相加)% 9 + 1。例如学生A学号后2位是80,则该数字为(8+0)% 9 + 1 = 9,那么生成的数独棋盘应如下(x表示满足数独规则的任意数字):测试
测试机为Windows环境,所以提交到Github上的项目均需要建立一个名字为BIN的文件夹,里面必须含有可执行文件(以exe为后缀)与相关的依赖库,请注意以下两点:
- 确保可执行文件的名字命名为 sudoku.exe。
- 确保生成的棋盘文件 sudoku.txt 与可执行文件在同一目录下,生成文件时请使用相对路径!
正确性测试中输入范围限制在 1-1000,要求程序在 60 s 内给出结果,超时则认定运行结果无效。
性能测试中输入范围限制在 10000-1000000,没有时间的最小要求限制,输入100w,要求在10分钟内给出结果。
PSP
| PSP | Personal Software Process Stages | 预估耗时(小时) | 实际耗时(小时) |
|---|---|---|---|
| Planning | 计划 | 1 | 0.5 |
| ·Estimate | · 估计这个任务需要多少时间 | 1 | 0.5 |
| Development | 开发 | 25 | 47 |
| · Analysis | · 需求分析 (包括学习新技术) | 5 | 4 |
| · Design Spec | · 生成设计文档 | 0.5 | 0 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 0 | 0 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 0 | 0 |
| · Design | · 具体设计 | 0.5 | 1 |
| · Coding | · 具体编码 | 16 | 24 |
| · Code Review | · 代码复审 | 1 | 3 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 2 | 15 |
| Reporting | 报告 | 5 | 7 |
| · Test Report | · 测试报告 | 2 | 2.5 |
| · Size Measurement | · 计算工作量 | 0.5 | 1 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 2.5 | 3.5 |
| 合计 | 31 | 54.5 |
(由于是第一次做PSP,最后发现实际耗时竟然比预估耗时多出那么多,安排的时间不是很充裕,到后面差点没做完,心态简直爆炸,还好赶出来了。)
算法及实现
看到题目,第一反应就是暴力解,但是冷静下来想想,这个显然是不现实的。后来看到百度上有提到用深搜和回溯法,大概看了一下,感觉太过麻烦。之后,受到同学的启发,打算采用投机取巧得方法,具体思路为:
先写一个符合要求的数独棋盘,然后通过各种矩阵变化,变出其他的数独棋盘并输出我的做法为:先构造一个满足要求的矩阵(由于使用9x9矩阵表示数独棋盘,下面都直接说矩阵),即满足数独规则且左上角为5的矩阵(我的尾号为13,按要求左上角需为5),如下
int sudo[9][9]={ //构造新数独棋盘的原始棋盘
{ 5, 6, 2, 8, 9, 3, 4, 7, 1 },
{ 8, 9, 7, 5, 1, 4, 6, 3, 2 },
{ 4, 1, 3, 2, 6, 7, 5, 9, 8 },
{ 6, 3, 8, 7, 5, 1, 9, 2, 4 },
{ 1, 7, 9, 6, 4, 2, 3, 8, 5 },
{ 2, 4, 5, 3 ,8 ,9 ,7 ,1, 6 },
{ 9, 2 ,6 ,4, 7, 8, 1, 5, 3 },
{ 7, 8, 4, 1, 3, 5, 2, 6, 9 },
{ 3, 5, 1, 9, 2, 6, 8, 4, 7 }
然后通过相关变化,生成其他矩阵,这里采用替换法、行变换和列变换三种:
替换法:通过一个一维数组来替换矩阵中各元素的位置,一维数组的元素为1-9九个数字,遍历矩阵,每一个矩阵点的数(假设为a)用一维数组中下标为a的元素替换。比如一维数组array[10]={0,1,2,3,4,5,6,7,8,9}(矩阵元素为1-9,故数组大小为10,舍弃第一个元素),遍历矩阵,sudo[0][0]=5,故将该元素换为array[5],即5,以此类推。发现在这种情况下,原矩阵没有发生改变,就可以将原矩阵输出。然后只要不断改变array[]元素的顺序,就可以生成不同的矩阵。理论上有9!种可能,即数字1-9的全排列。对于全排列,有一个next_permutation(str.begin(), str.end())的库函数可以用,使用时要加上#include<algorithm>。值得注意的是,该函数返回一个布尔值,它的两个参数均为字符型,其中str为string型,所以要将字符转化为数字。另外,为了达到左上角为5的要求,只要保证array[4]=='5'即可,生成数组array[]的代码如下:
……
while (next_permutation(str.begin(), str.end()) &&str[4]=='5')
{
/**
next_permutation(str.begin(), str.end())
函数可以将字符串进行全排列,
使用时要包含algorithm头文件。
另外,要求棋盘左上角为座号后两位相加对9取模再加一,
我的尾号为13,所以左上角恒为5。
*/
for (int i = 1; i <= 9; i++)//
{
array[i] = str[i - 1] - 48;
}
break;
}
……
替换代码为:
……
int *ptr = aryGene.toGenerate(); //获取随机数组
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
sudo[i][j] = ptr[sudo[i][j]]; //构造新棋盘
}
}
……
行变换:根据矩阵的行变换生成新的矩阵,为了保证左上角为5,第一行不进行交换,为了使变换后的矩阵符合数独规则,行变换只在组内进行,根据行号为分为012、345、678三组,为了方便,第一组均不进行交换。
行变换代码:
……
for (int row = 3; row < 9; row++)
{
for (int i = 0; i < 9; i++)
{
swap(sudo[row % 3 + 3][i], sudo[(row + 1) % 3 + 3][i]);
}
……
}
for (int row = 6; row < 12; row++)
{
for (int i = 0; i < 9; i++)
{
swap(sudo[row % 3 + 6][i], sudo[(row + 1) % 3 + 6][i]);
}
……
}
……
列变换:根据矩阵的列变换生成新的矩阵,为了保证左上角为5,第一列不进行交换,为了使变换后的矩阵符合数独规则,列变换只在组内进行,根据列号为分为012、345、678三组,为了方便,第一组均不进行交换。
列变换代码:
……
for (int line = 3; line < 9; line++)
{
for (int i = 0; i < 9; i++)
{
swap(sudo[i][line % 3 + 3], sudo[i][(line + 1) % 3 + 3]);
}
……
}
for (int line = 6; line < 12; line++)
{
for (int i = 0; i < 9; i++)
{
swap(sudo[i][line % 3 + 6], sudo[i][(line + 1) % 3 + 6]);
}
……
}
……
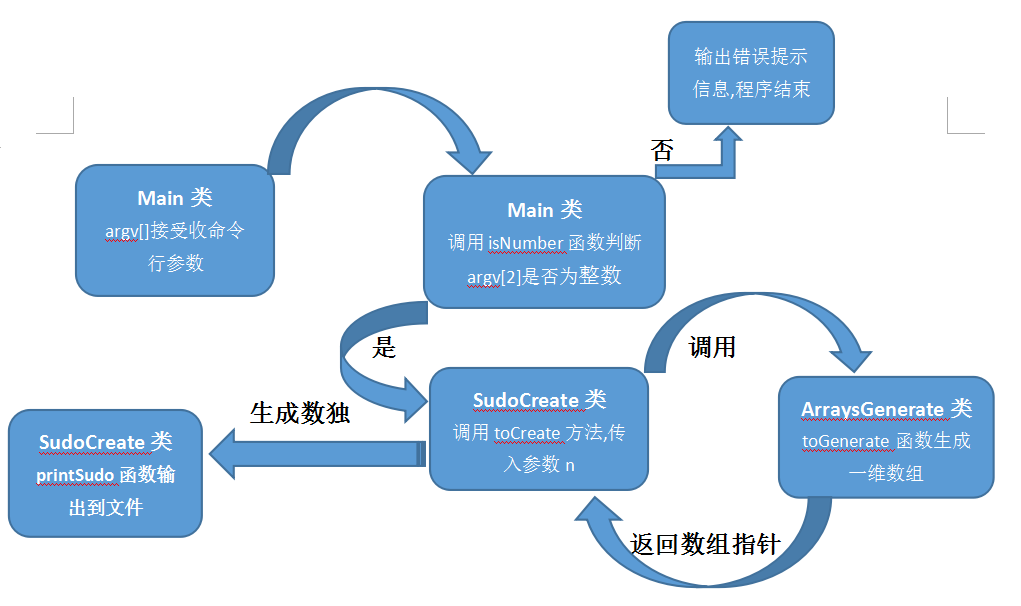
基于这种思路,我的项目分为5个文件,2个.h文件和3个.cpp文件。包含两个类:ArrayGenerate和SudoCreate。
ArrayGenerate: 包含一个方法int* toGenerate(),用以生成上述一维数组。
SudoCreate:包含void toCreate(int n)方法,用以生成矩阵,void printSudo()方法,用以打印矩阵。
Main:包含bool isNumber(string str)方法,判断命令行第三个参数是否为正整数,从而确定是否为有效命令,对于命令的处理如下:
……
str1 = argv[1];
str2 = argv[2];
if (argc != 3 || (argc==3&&(str1 != "-c" || !isNumber(str2)))) //错误命令判断
{
cout << "输入错误命令" << endl;
}
else
{
sstream.clear();
sstream << str2;
sstream >> n; //获取棋盘数量N
sudoCrt.toCreate(n);
}
……
各类和函数之间的调用关系如下图所示:
命令行运行.exe文件以及文件输出
命令行运行.exe文件
main()函数主要形式为:
(1) int main( ) ,一般方式。
(2) int main( int argc , char *argv[ ] ),这里采用此种方式。
其参数argc和argv[ ]用于运行时,把命令行参数传入主程序,参数具体含义如下:
int argc:英文名为arguments count(参数计数)
运行程序传送给main函数的命令行参数总个数,包括可执行程序名,其中当argc=1时表示只有一个程序名称,此时存储在argv[0]中.
char *argv[ ]:英文名为arguments value/vector(参数值)
字符串数组,用来存放指向字符串参数的指针数组,每个元素指向一个参数,空格分隔参数,其长度为argc,数组下标从0开始,argv[argc]=NULL。
argv[0] 指向程序运行时的全路径名,这里即为“sudoku.exe”
argv[1] 指向程序在DOS命令中执行程序名后的第一个字符串,这里即为“-c”
argv[2] 指向执行程序名后的第二个字符串,这里即为矩阵个数N,需要把字符串转化为整型数,转化方法见上面代码。
argv[argc] 为NULL。
文件输出
文件输出有多种方式,这里采用的是C++文件流输出:
fstream outfile("sudoku.txt", ios::out); //创建文件流对象,out为覆盖上次运行结果
if(outfile.is_open())
{
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
outfile << sudo[i][j] << ' ';
}
outfile << endl;
}
outfile << endl;
}
性能分析及优化
使用vs2017的性能探查器进行性能测试,测试报告结果如下:
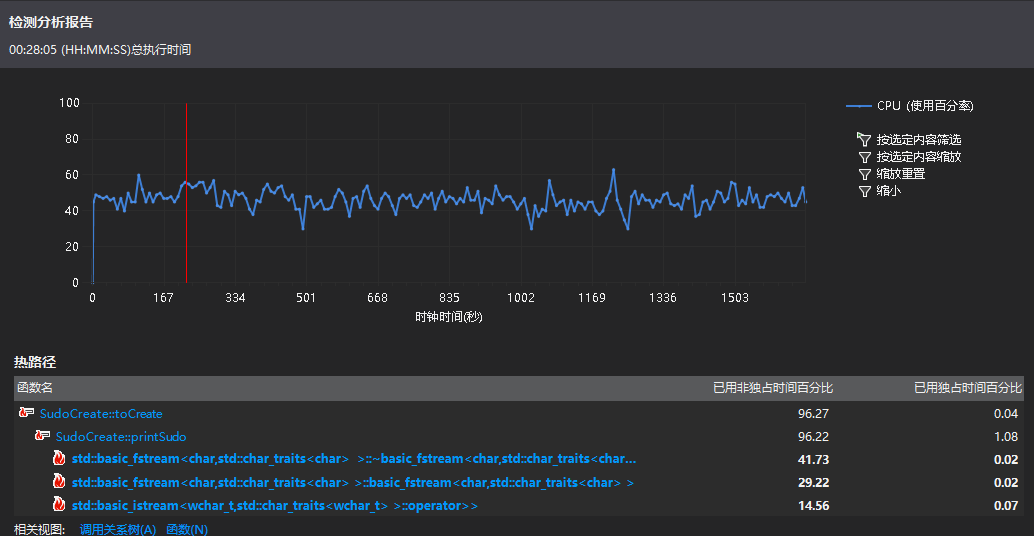

发现,发现程序运行时间过长,需要优化,用以输出矩阵的函数printSudo调用次数特别多,要加快运行速度,可以从这个函数着手,所以返回源代码去查看。原代码如下:
void SudoCreate::printSudo() //输出新棋盘
{
fstream outfile("sudoku.txt", ios::app); //创建文件流对象,app为追加到文件末尾
if(outfile.is_open())
{
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
outfile << sudo[i][j] << ' ';
}
outfile << endl;
}
outfile << endl;
}
}
从上述代码可以看出,每一次调用printSudo函数时,都会重新创建文件流对象,并且打开文件,100w个矩阵就要打开100w次文件,这样就导致大量的时间耗在打开文件上,实际上只要打开一次就好。遂作如下修改:
fstream outfile("sudoku.txt", ios::out); //创建文件流对象,out为覆盖上次运行结果
void SudoCreate::printSudo() //输出新棋盘
{
//fstream outfile("sudoku.txt", ios::app); //创建文件流对象,app为追加到文件末尾
if(outfile.is_open())
{
for (int i = 0; i < 9; i++)
{
for (int j = 0; j < 9; j++)
{
outfile << sudo[i][j] << ' ';
}
outfile << endl;
}
outfile << endl;
}
}
现在重新进行测试,结果如下:

可以看出运行速度明显提升。
单元测试及代码覆盖率
单元测试
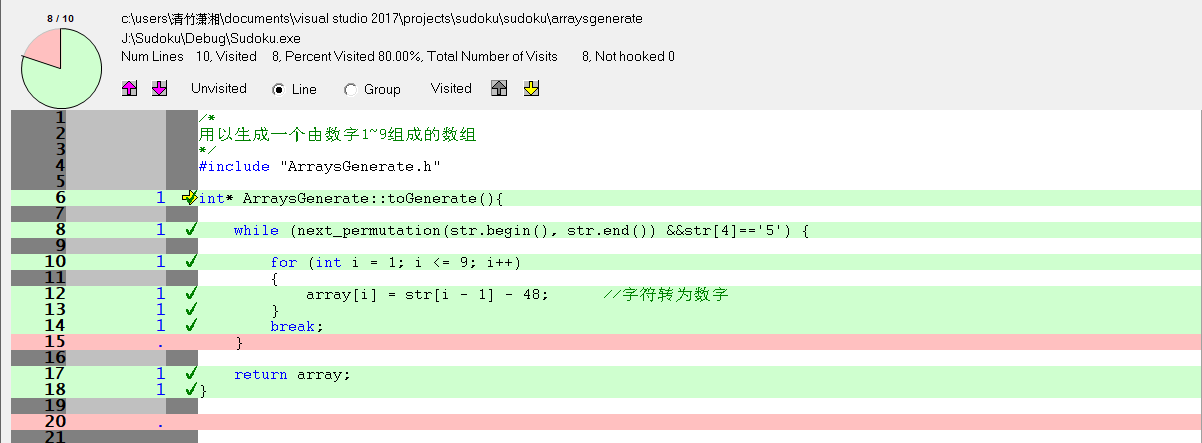
就写了一个测试,测试toGenerate函数,该函数的作用是生成一个一维数组,数组元素由数字1-9组成,且a[5]=5。
测试代码如下:
#include "stdafx.h"
#include "CppUnitTest.h"
#include "../Sudoku/ArraysGenerate.h"
using namespace Microsoft::VisualStudio::CppUnitTestFramework;
namespace UnitTest1
{
TEST_CLASS(UnitTest1)
{
public:
TEST_METHOD(TestToGenerate)
{
// TODO: 在此输入测试代码
int *ptr;
ArraysGenerate arryGen;
ptr = arryGen.toGenerate();
Assert::AreEqual(isCorrect(ptr), 1);
}
int isCorrect(int a[]) //检查生成数组是否为以数字1-9为元素且每个数字仅出现一次
{
int cnt[10] = { 0 };
int i;
for (i = 1; i <= 9; i++)
{
if (a[i] < 1 || a[i]>9 || a[5] != 5)
return 0;
cnt[a[i]]++;
}
for (i = 1; i <= 9; i++)
{
if (cnt[i] != 1)
break;
}
if (i == 10)
return 1;
else
return 0;
}
};
}
测试结果

代码覆盖率
代码覆盖率是本次作业最虐的地方,花了1天半都没做好。一开始用vs2017企业版的做,总是出不了结果,截图如下

百般折腾还是出不来,后来参考助教给的教程(链接),好像是出来了,我也不太确定,反正截图如下:


阅读《构建之法》的收获及本次作业总结
本次作业总结为以下几点:
- github的使用,在之前的《C++面向对象程序设计》课程中已经使用过,简单点。
- 《构建之法》的阅读,重点。
- 生成不重复的已解答数独棋盘的算法及实现,难点。
- 命令行运行.exe文件以及文件输出,之前接触过,熟悉点。
- 性能测试及优化,陌生点。
- 单元测试及代码覆盖率分析,麻烦点。
对于1、4之前接触过,并没有什么新的收获。本次主要收获来自于《构建之法》以及对性能测试、单元测试和代码覆盖率的了解。通过阅读《构建之法》,学会了做PSP,知道一个项目从开始到结束要经历怎样的过程,了解什么是性能测试和单元测试。
性能测试对于程序的重要性不言而喻,但为什么要进行单元测试呢?最后能出结果不就行了吗?我的理解是:单元测试是对某个具体的单元(一个类或是一个方法)进行正确性测试,单元测试通过可以增加自己的信心。诚然,在简单的程序中,单元测试的作用并不明显,比如写一个计算a+b的程序,单元测试就没有太大的必要。但是,如果是一个大项目,需要大量的类和方法,那么如果不进行单元测试,结果出错了又该到哪里去找呢?又或是自己是否曾有过不知道自己写的方法到底能不能实现自己的要求的困扰呢?如果在写程序的时候进行单元测试,测试通过了,我们就有足够的信心往下继续写,当结果出错时,那些测试通过的部分显然不是查错的重点,这样的话,单元测试的作用就特别明显了。
在进行单元测试的过程中,遇到了一个问题,就是当我在vs2017(企业版)写完测试代码,要进行测试时,出现“无法解析的外部符号”的错误,在网上搜索修改的方法都没有用,后来看到一篇博客(链接),发现上面出现跟我我一模一样的错误,就按照上面的改,还是没成功。折腾了一早上,后来把方法的实现放到了头文件里,即在头文件中同时给出方法的声明和实现,这样就通过了测试。虽然通过了测试,但还是不明白为什么会这样。明明方法的实现是可以放到.cpp文件里,但为什么单元测试时就是不行。而且为什么别人可以,我的就有问题,难道这还看人品?难受。
另外,对于单元测试还有另外一个疑问:以前在编程的时候,对于某个函数如果不确定它是否能得到想要的输出,会用另一个编译器单独写一下那个函数来进行测试,这算不算是另类的单元测试呢?如果是,那么这两种单元测试方法的优劣性如何。个人觉得,自己以前得方法比较简单,只要加上一些输入输出语句然后把函数复制粘贴就好了,但是vs的单元测试还要进行各种操作,甚是麻烦,而且还可能出现各种问题,所以到底该如何去看待单元测试呢?
关于vs的单元测试代码,最后都要用到一个验证函数Assert.AreEqual ,这里给出这个函数的重载列表:

最后附加一则求组队告示:
《构建之法》第三章提到团队对个人的期望,具体如下:
1.交流:能有效的和其他队员交流,从大的技术方向,到看似微小的问题。
2.说到做到:就像上面说的“按时交付”
3.接受团队赋予角色要求工作:团队要完成任务,有很多事情要做,是否能接受不同的任务并高质量完成?
4.全力投入团队的活动:就像一些评审会议,代码复审,都要全力以赴地参加,而不是游离于团队之外。
5.按照团队流程的要求工作:团队有自己的流程(见“团队和流程”一章),个人的能力即使很强,也要按照团队制定的流程工作,而不要认为自己不受流程的约束
6.准备:在开会讨论之前,开始一个新功能之前,一个新项目之前,都要做好准备工作。
7.理性地工作:软件开发有很多个人的、感情驱动的因素,但是一个成熟的团队成员必须从事实和数据出发,按照流程,理性地工作。很多人认为自己需要灵感和激情,才能为宏大的目标奋斗,才能成为专业人士,著名的艺术家说Chuck Close说:我总觉得灵感是属于业余爱好者的,我们职业人士只是每天持续工作。今天你继续昨天的工作,明天你继续今天的工作,最终你会有所成就。
首先声明以上要求我都可以做到,然后求组队。

