树的总结
思维导图
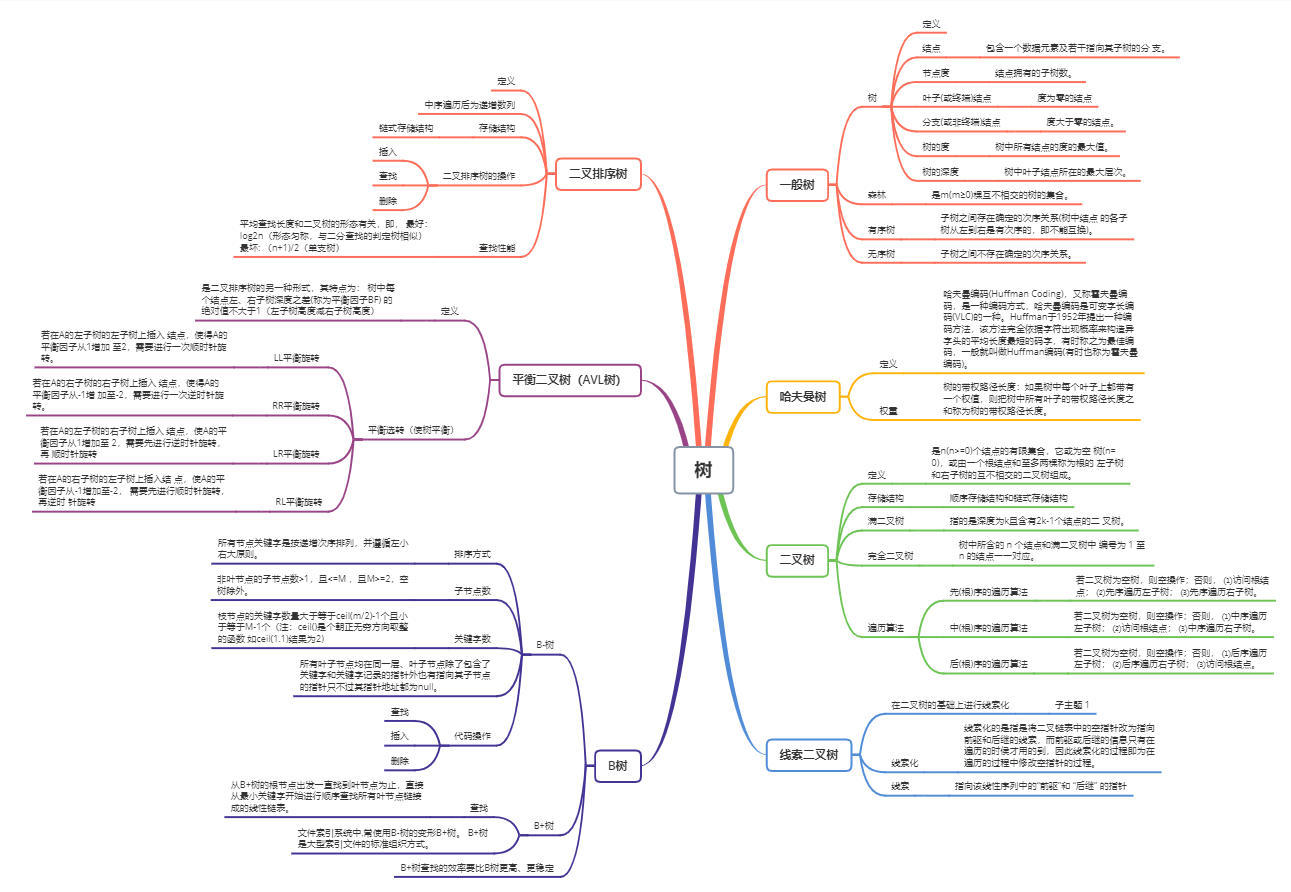
重要概念
二叉树的性质
性质1 :在二叉树的第 i 层上至多有2i-1 个结 点(i≥1)。
性质2:深度为 k 的二叉树上至多含 2k-1 个结 点(k≥1)。
性质3:对任何一棵二叉树,若它含有n0 个叶子 结点、n2 个度为2的结点,则必存在关系式:n0 = n2+1。
B-树
性质:
1.每个节点至多m个孩子节点(至多有m-1个关键字) 。
2.除根节点外,其他节点至少有m/2个孩子节点(即 至少有m/2-1个关键字)。
3.若根节点不是叶子节点,根节点至少两个孩子节点。
插入:
关键字 插入的位置必定在最下层的非叶结点,插入后,该结点的关键字个数n<m,不修改指针,插入后,该结点的关键字个数 n=m,则需进行 “结点分裂”,令 s = m/2,在原结点中保留 (A0,K1,…… , Ks-1,As-1);建新结点(As, Ks+1,…… ,Kn,An);将(Ks, p)插入双亲结点,若双亲为空,则建新的根结点。
二叉树中序遍历的非递归算法的代码
void LevelTraversal(queue<BiTree>& que, BiTree T)
{
int count = 0;
que.push(T);
while (!que.empty())
{
if (que.front()->lchild) {
que.push(que.front()->lchild);
}
if (que.front()->rchild) {
que.push(que.front()->rchild);
}
if (count == 0) {
cout << que.front()->data;
count = 1;
}
else {
cout << " " << que.front()->data;
}
que.pop();
}
}
求二叉树树的高度
int GetHeight(BinTree BT)
{
int LH, RH;
if (!BT)
return 0;
else
{
LH = GetHeight(BT->Left);
RH = GetHeight(BT->Right);
return LH > RH ? ++LH : ++RH;
}
}
二叉树的层次遍历
void LevelTraversal(BiTree T)
{
int count = 0;
queue<BiTree> que;
que.push(T);
while (!que.empty())
{
if (que.front()->lchild) {
que.push(que.front()->lchild);
}
if (que.front()->rchild) {
que.push(que.front()->rchild);
}
if (count == 0) {
cout << que.front()->data;
count = 1;
}
else {
cout << " " << que.front()->data;
}
que.pop();
}
}
二叉排序树建立,查找,插入,删除伪代码及代码实现
#include <iostream>
using namespace std;
#include <stdio.h>
typedef struct BiTNode
{
int data;
struct BiTNode* lchild, * rchild;
}BiTNode, * BiTree;
void Delete(BiTNode*& p);
void Delete1(BiTNode* p, BiTNode* &r);
/*SearchBst(T, key) {
if (T为空 || T->data等于key)
return T;
if (T->data小于key)
SearchBst(T->lchild, key);
else
SearchBst(T->rchild, key);
}*/
BiTNode*SearchBST(BiTNode *T, int key)
{
if (T==NULL|| T->data == key)
return T;
if (T->data<key)
SearchBST(T->lchild, key);
else
SearchBST(T->rchild, key);
}
/*InsertBST(T, key) {
if (T等于空) {
T->data == key;
T->lchild == T->rchild = NULL;
}
else {
if (T->data等于key)return;
else {
if (key小于T->data) {
插入左子树
InsertBST(T->lchild, key);
}
else 插入右子树
InsertBST(T->rchild, key);
}
}*/
void InsertBST(BiTNode* &T, int key)//建立二叉排序树
{
if (T == NULL) {
T = new BiTNode;
T->data = key;
T->lchild = T->rchild = NULL;
}
else {
if (T->data == key)return;
else if (key < T->data) {
return InsertBST(T->lchild, key);
}
else {
return InsertBST(T->rchild, key);
}
}
}
/*CreateBST(T)
{
int a[100];
int i=0;
BiTree* T = NULL;
char ch;
do {
i++;
读入数字到数组a中
插入到二叉树中
} while (读入一个字符判断是否到结尾);
return T;
}*/
BiTNode *CreateBST()
{
int a[100];
int i=-1;
BiTNode* T = NULL;
char ch;
do {
i++;
cin >> a[i];
InsertBST(T, a[i]);
} while ((ch = getchar()) != '\n');
return T;
}
/*DeleteBST(T, key)
{
if (T为空) {
return 0;
}
else {
if (key小于T->data) DeleteBST(T->lchild, key);
递归在左子树中删除key的节点
else if (key小于T->data) DeleteBST(T->rchild, key);
递归在右子树中删除key的节点
else {
进入Delete(T)删除节点
return 1;
}
}
}*/
int DeleteBST(BiTNode* &T, int key)
{
if (T==NULL) {
return 0;
}
else {
if (key < T->data) {
return DeleteBST(T->lchild, key);
}
else {
if (key > T->data) {
return DeleteBST(T->rchild, key);
}
else {
Delete(T);
return 1;
}
}
}
}
/*Delete(p)
{
定义一个节点q
if (p的右子树为空) {
q = p;
p等于p的左子树
free(p);
}
else {
if (p的左子树为空) {
q = p;
p等于p的右子树
free(q);
}
else {
既有左右子树,进入Delete1(p, p->lchild)函数
}
}
}*/
void Delete(BiTNode*& p)
{
BiTNode* q;
if (p->rchild==NULL) {
q = p;
p = p->lchild;
free(q);
}
else {
if (p->lchild == NULL) {
q = p;
p = p->rchild;
free(q);
}
else {
Delete1(p, p->lchild);
}
}
}
/*Delete1(p, r)
{
定义节点q
if (r右子树不为空) {
接着查找p的左子树的最右下节点Delete1(p, r->rchild);
}
else {
p->data = r->data;
q = r;
r等于r的左子树
free(q);
}
}*/
void Delete1(BiTNode* p, BiTNode* &r)
{
BiTNode* q;
if (r->rchild != NULL) {
Delete1(p, r->rchild);
}
else {
p->data = r->data;
q = r;
r = r->lchild;
free(q);
}
}
void InOrderTraverse(BiTree T)//中序遍历
{
if (T == NULL)
return;
InOrderTraverse(T->lchild);
cout << T->data << " ";
InOrderTraverse(T->rchild);
}
int main()
{
BiTree BST = CreateBST();
cout << "中序遍历:";
InOrderTraverse(BST);
cout << endl;
cout << "请输入你要清除的数字" << endl;
int n;
cin >> n;
int cont = DeleteBST(BST, n);
if (cont == 0) {
cout << "数字不存在" << endl;
}
else {
cout << "清除成功" << endl;
}
cout << "中序遍历:";
InOrderTraverse(BST);
return 0;
}
疑难问题及解决方案
根据后序和中序遍历输出先序遍历(PTA)
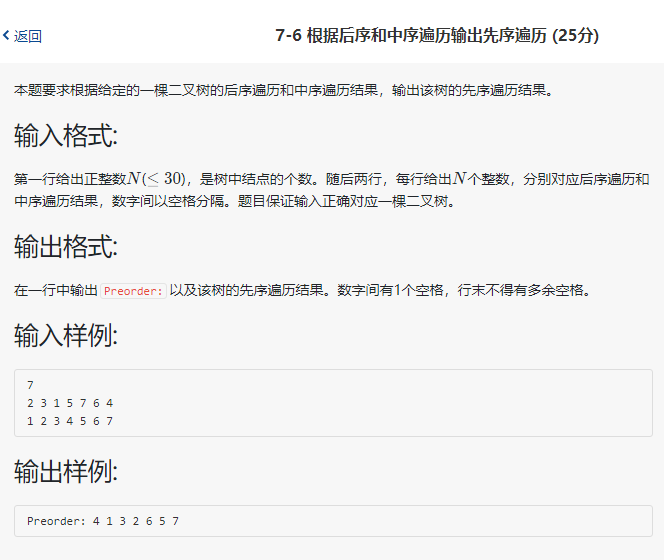
由题意,必须先理解后序遍历和中序遍历结果对应的二叉树是怎么样,先把根确定,在确定根的左子树和右子树,然后进去根的左子树,右子树,在确定左子树和右子树的样子,从上向下确定整个二叉树。
#include<iostream>
using namespace std;
int in[31],post[31];
typedef struct BiTNode{
int data;
struct BiTNode *lchild;
struct BiTNode *rchild;
}BiTNode,*BiTree;
BiTree Build(int *in,int *post,int n)
{
if(n <= 0)
return NULL;
int *p = in;
while(p){
if(*p == *(post + n - 1))
break;
p++;
}
BiTree T = new BiTNode;
T->data = *p;
int len = p - in;
T->lchild = Build(in,post,len);
T->rchild = Build(p + 1,post + len,n - len - 1);
return T;
}
void PreOrder(BiTree T){
if(T){
printf(" %d",T->data);
PreOrder(T->lchild);
PreOrder(T->rchild);
}
return;
}
int main(){
int n;
BiTree T;
scanf("%d",&n);
for(int i = 0;i < n;i++)
scanf("%d",&post[i]);
for(int i = 0;i < n;i++)
scanf("%d",&in[i]);
T = Build(in,post,n);
printf("Preorder:");
PreOrder(T);
return 0;
}
疑难问题
1.B-树和B+树怎么创建?
2.有没有更好的树的算法?


