数据结构已学知识总结

思维导图

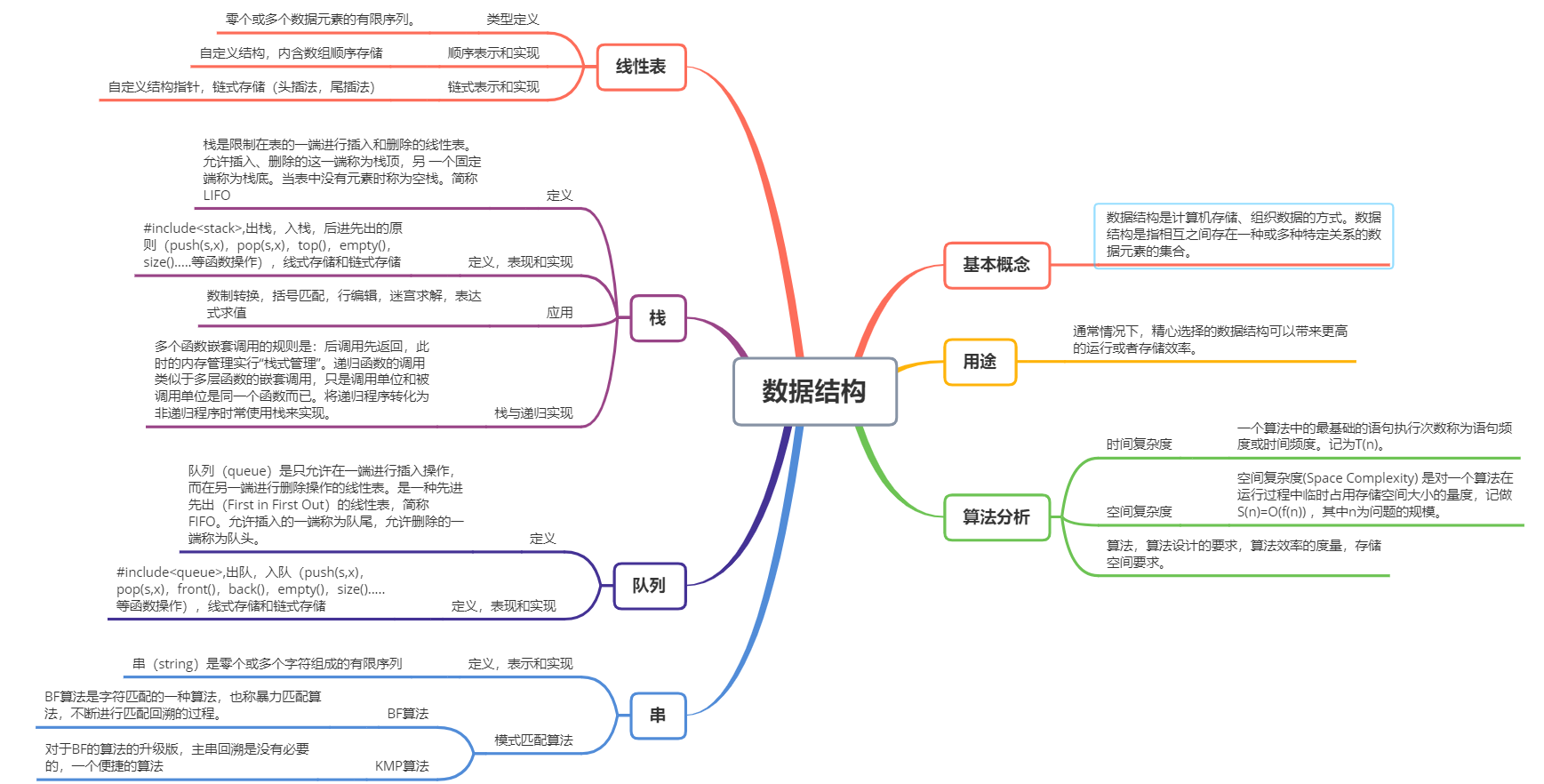
重要概念

1.线性表

(1)顺序存储

struct LNode{
	ElementType Data[MAXSIZE];
	Position Last;
};
typedef PtrToLNode List;
//List L;
 
//初始化
List MakeEmpty(){
	List L;
	L = (List)malloc(sizeof (struct LNode));
	L->Last = -1;
	return L;
} 
 
//查找
//#define ERROR -1
Position Find(List L,ElementType X){
	Position i = 0;
	while(i<=L->Last&&L->Data[i]!=X){
		i++;
	}
	if(i>L->Last) printf("您查找的数不存在\n");
	else printf("您查找数的存储下标为：%d",i);
}
 
//插入
bool Insert(List L ,ElementType X,int i){
	Position j;
	//表空间已满，不能插入 
	if(L -> Last == MAXSIZE-1){
		printf("表满");
		return false;
	}
	//检查插入位序的合法性：是否在1~n+1.
	if(i<1||i>L->Last+2){
		printf("位序不合法");
		return false;
	} 
	for(j=L->Last;j>=i-1;j--){
		L->Data[j+1] = L-> Data[j];
	}
	L->Data[i-1] = X;
	L->Last++;
	return true;
} 
 
//删除
bool Delete(List L,int i){
	Position j;
	if(i<1||i>L->Last+1){
		printf("位序%d不存在元素\n",i);
	}
	else{
		for(j=i;j<=L->Last;j++){
			L->Data[j] = L->Data[j+1];
		}
		L->Last--;
		printf("删除成功\n");
	}
	
} 
 
//求表长
int Length(List L){
	return L->Last+1;
}

(2)链式存储

void DestroyList(LinkList &L)
{
	LinkList p = L;
	while (L)
	 {
		p = L;
		L = L->next;
		delete p;
	 }
}

void CreateListF(LinkList& L, int n)//头插法建链表，L表示带头结点链表，n表示数据元素个数
{
	int i;
	LinkList p;
	L = new LNode;
	L->next = NULL;
	for (i = 0; i < n; i++) {
		p = new LNode;
		cin >> p->data;
		p->next = L->next;
		L->next = p;
	}
}

void CreateListR(LinkList& L, int n)//尾插法建链表，L表示带头结点链表，n表示数据元素个数
{
	int i;
	LinkList head, p;
	L = new LNode;
	head = L;
	for (i = 0; i < n; i++) {
		p = new LNode;
		cin >> p->data;
		head->next = p;
		head = p;
	}
	head->next = NULL;
}

2.栈和队列

1、stack

用数据结构c++中自带的头文件中

定义stack对象的示例代码如下：

stack s1;stack s2;

stack的基本操作有：

1.入栈，如例：s1.push(x);

2.出栈，如例：s1.pop();注意，出栈操作只是删除栈顶元素，并不返回该元素。**

3.访问栈顶，如例：s1.top()

4.判断栈空，如例：s1.empty()，当栈空时，返回true。

5.访问栈中的元素个数，如例：s1.size()

2、queue

用数据结构c++中自带的头文件中。

queue q1;queue q2;

queue的基本操作有：

1.入队，如例：q1.push(x); 将x接到队列的末端。

2.出队，如例：q1.pop(); 弹出队列的第一个元素，注意，并不会返回被弹出元素的值。

3.访问队首元素，如例：q1.front()，即最早被压入队列的元素。

4.访问队尾元素，如例：q1.back()，即最后被压入队列的元素。

5.判断队列空，如例：q1.empty()，当队列空时，返回true。

6.访问队列中的元素个数，如例：q1.size()

3.串

(1)BF算法

BF(Brute Force)算法是普通的模式匹配算法，BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配，若相等，则继续比较S的第二个字符和 T的第二个字符；若不相等，则比较S的第二个字符和T的第一个字符，依次比较下去，直到得出最后的匹配结果。

int BF(char S[],char T[],int pos)
{//c从第pos位开始搜索匹配
    int i=pos,j=0;
    while(S[i+j]!='\0'&&T[j]!='\0')
    {
        if(S[i+j]==T[j])
            j++;
        else
        {
            i++;
            j=0;
        }
    }
    if(T[j]=='\0')
        return i+1;
    else
        return -1;
}

(2)KMP算法

//建立模式串的next数组
void GetNext(char* p, int next[])
{
	int pLen = strlen(p);
	next[0] = -1;
	int k = -1;
	int j = 0;
	while (j < pLen - 1)
	{
		if (k == -1 || p[j] == p[k])
		{
			++k;
			++j;
			next[j] = k;
		}
		else
		{
			k = next[k];
		}
	}
}
//进行主串和模式串匹配
void getNext(const char* pattern,int next[])
{
       next[0]=   -1;
       int k=-1,j=0;
       while(pattern[j] != '\0')
       {
              if(k!= -1 && pattern[k]!= pattern[j] )
                     k=next[k];
              ++j;++k;
              if(pattern[k]== pattern[j])
                     next[j]=next[k];
              else
                     next[j]=k;
       }
}

疑难问题及解决方案

1.队列

银行业务队列简单模拟

由题目可以来理清思路，建立AB两个队列，分别将编号以偶数和非偶数存储在AB两个队列，然后将按照输出要求，先输出两个A队列的编号，在输出B队列的一个编号，判断两个队列是否为空，当A或B队列为空，就退出，将A或B中剩下的队列全部输出。

代码如下：

#include<iostream>
#include<stdio.h>
#define MAXSIZE 1000
#define OVERFLOW -2
#define OK 1
#define ERROR -1
using namespace std;

//定义队列，有头位置和尾位置记录
typedef struct
{
	int* base;
	int front;
	int rear;
} SqQueue;

//新建一个队列
int InitQueue(SqQueue& Q)
{
	Q.base = new int[MAXSIZE];
	if (!Q.base)
		return OVERFLOW;
	Q.front = Q.rear = 0;
	return OK;
}

//出队列的一个元素，存储在e中。
int DeQueue(SqQueue& Q, int& e)
{
	if (Q.front == Q.rear)
		return ERROR;
	e = Q.base[Q.front];
	Q.front = (Q.front + 1) % MAXSIZE;
	return OK;
}

//将数组中编号遍历输出。
void Print(int* arr, int n)
{
	cout << arr[0];
	for (int i = 1; i < n; i++)
		cout << " " << arr[i];
}

int main()
{
	SqQueue A, B;
    //新建AB两个队列存储编号
	InitQueue(A);
	InitQueue(B);
    
	int N, data, tmp, i = 0;
	cin >> N;
	int result[N];
    
	for (int i = 0; i < N; i++)
	{
		cin >> data;
        
		if (data % 2 != 0)//判断不为偶数存储在A队列
		{
			if ((A.rear + 1) % MAXSIZE == A.front)
				return ERROR;
			A.base[A.rear] = data;
			A.rear = (A.rear + 1) % MAXSIZE;
		}
		else//判断为偶数存储在B队列
		{
			if ((B.rear + 1) % MAXSIZE == B.front)
				return ERROR;
			B.base[B.rear] = data;
			B.rear = (B.rear + 1) % MAXSIZE;
		}
        
	}
    
    //当AB两个队列都不为空，将两个A队列头元素，一个B队列头元素，存储在result数组中。
	while ((A.front != A.rear) && (B.front != B.rear)   
	{
		DeQueue(A, tmp);
		result[i++] = tmp;
		DeQueue(A, tmp);
		result[i++] = tmp;
		DeQueue(B, tmp);
		result[i++] = tmp;
        
	}
    
    //如果A队列不为空，将A队列元素存储在result数组中
	while (A.front != A.rear)
	{
        
		DeQueue(A, tmp);
		result[i++] = tmp;
	}
           
    //如果B队列不为空，将B队列元素存储在result数组中
	while (B.front != B.rear)
	{
		DeQueue(B, tmp);
		result[i++] = tmp;
        
	}
           
    //输出result数组
	Print(result, N);
           
    return 0；
}

2.实现KMP算法

由所学知识来看这个题目，要用到KMP算法，由我们理解的KMP算法的精髓部分，我们还需要将他们总结起来，能够实现具体功能，才能说是做好了，所以自己写出整体代码，是什么重要的。