线性同余法生成(0,1)均匀分布随机数并进行均匀性和独立性检验,舍选法生成符合特定概率密度的随机数
题目
用舍选法在计算机中产生概率密度函数为
\(f(x)=\left\{\begin{array}{l}
\frac{12}{(3+2 \sqrt{3}) \pi}\left(\frac{\pi}{4}+\frac{2 \sqrt{3}}{3} \sqrt{1-x^{2}}\right), 0 \leq x \leq 1 \\
0
\end{array}\right.\)
的100个随机数,具体要求:
(1)[0,1]均匀分布随机数用线性同余法产生,参数由自己确定,不能用计算语言已有的函数。
(2)对用线性同余法产生的(0,1)均匀随机数进行均匀性和独立性检验,检验样本为100个。
(3)计算舍选法的理论上舍选效率和实际仿真的舍选效率。
程序与分析
函数定义
# 线性同余法产生n个服从(0,1)均匀分布的随机数
import time
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import rcParams
# 设置字体为楷体
rcParams['font.sans-serif'] = ['KaiTi']
# 函数avg_random(n)产生n个服从(0,1)均匀分布的随机数
def avg_random(n):
a = 32310901 # 乘子
c = 1729 # 增量
M = pow(2, 32)
theats = []
x0 = time.time() # 以时间戳为种子
xi = x0
for i in range(0, n):
xi = (a * x0 + c) % M
theati = xi / M
theats.append(theati)
x0 = xi
theats = np.array(theats)
return theats
# 1. 对产生的随机数进行粗略检验,如果偏差超过10%,提示生成的随机数均匀性很差,不进一步进行检验
# 粗略检验函数rough_test()检验通过返回True,失败返回False
def rough_test(theats):
mean = np.average(theats)
sec = np.average(theats * theats)
if np.abs(mean - 0.5) / 0.5 < 0.1 * 0.5 or np.abs(sec - (1 / 3)) < 0.1 * (1 / 3):
return True
else:
return False
# 2. 粗略检验通过后,进行频率检验
# 频率检验函数frequency_test(),参数"sec_num"为区间个数,默认值为"10",检验通过(置信度取5%)返回True,失败返回False
def frequency_test(theats, sec_num=10):
N = len(theats) # 抽样值的个数
m = N / sec_num # 理论频数
sec_val = np.zeros(sec_num)
# 计算每个区间的实际频数
for theat in theats:
for i in range(1, 11):
if theat < (i / sec_num):
sec_val[i - 1] += 1
break
C = np.sum(np.square(sec_val - m) / m)
# 采用5%置信度的9自由度卡方分布上分位数为16.919
if C < 16.919:
return True
else:
return False
# 3. 独立性检验--相关系数检验,返回距离为distance(默认值为5)的两个随机数的相关系数
def corr_coeffient_test(theats, distance=5):
distance = np.abs(int(distance)) # 均值限制为正整数
mean = np.average(theats) # 样本均值
std = np.var(theats) # 样本方差
sumval = 0
for i in range(0, len(theats) - distance):
temp = theats[i] * theats[i + distance]
sumval += temp
R = (sumval / (len(theats) - distance) - pow(mean, 2)) / (pow(std, 2))
return R
# 4. 独立性检验--联立表检验,参数"k"为正方形每个维度被分割的个数(默认为4),参数"e"为数据偏离位数(默认为5),val_alpha为5%置信度k^2-1自由度卡方分布上分位数(默认25);随机数在独立性上95%可信则返回True,反之返回False
def simu_table_test(theats, k=4, e=5, val_alpha=25):
sec_val = np.zeros((k, k))
for i, j in zip(range(0, len(theats)), np.roll(range(0, len(theats)), -e)):
for x in range(1, k + 1):
if theats[i] < (x / k):
for y in range(1, k + 1):
if theats[j] < (y / k):
sec_val[x - 1][y - 1] += 1
break
break
C = 0
for i in range(0, k):
for j in range(0, k):
c = pow((sec_val[i][j] - np.sum(sec_val, 1)[i] * np.sum(sec_val, 0)[j] / len(theats)), 2) / (np.sum(sec_val, 1)[i] * np.sum(sec_val, 0)[j] / len(theats))
C += c
if C < val_alpha:
return True
else:
return False
# 密度函数
def fuc(x):
return 12 / ((3 + 2 * np.sqrt(3)) * np.pi) * (np.pi / 4 + 2 * np.sqrt(3) / 3 * np.sqrt(1 - pow(x, 2)))
# 函数rejection_method(R1,R2,n)产生n个服从题目密度函数分布的随机数,R1、R2为两个服从(0,1)均匀分布的随机数,同时返回理论效率'theory_efficience'和仿真效率'emulational_efficience'
def rejection_method(randow_num_list, n):
a = 0#函数下界
b = 1#函数上界
M = fuc(0)#函数最大值
X = []#随机数初始化
num = 0#随机数数量初始化
step=0#
failnum = 0
addstep=0
while num <n:
if not step%10:
addstep+=1
R1 = randow_num_list[step % (len(randow_num_list))]
R2 = randow_num_list[(step+addstep) % (len(randow_num_list))]
x = a + (b - a) * R1
if M * R2 <= fuc(x):
num += 1
X.append(x)
else:
failnum += 1
step+=1
return {'obje_randow_list': np.array(X), 'theory_efficience': 1 / (M * (a + b)), 'emulational_efficience': n / (n + failnum)}
生成100个服从(0,1)均匀分布的随机数并进行粗略检验
\(\frac{1}{N} \sum_{i=1}^{N} R_{i} \approx \frac{1}{2}\)
\(\frac{1}{N} \sum_{i=1}^{N} R_{i}^{2} \approx \frac{1}{3}\)
\(R_i\)为随机数,N为随机数个数,如果两个都明显不成立,就可否定随机性不够要求。
randow_num_list = avg_random(100)
if rough_test(randow_num_list):
print("粗略检验通过!\n随机数组为:\n ", randow_num_list)
else:
print("粗略检验失败!\n随机数组为:\n", randow_num_list)
输出结果:
粗略检验通过!
随机数组为:
[0.85159487 0.38553153 0.09123632 0.80387689 0.66494775 0.86175315
0.74260715 0.99250419 0.76666027 0.18396305 0.75009426 0.5288669
0.11249721 0.23132686 0.37451616 0.54591484 0.46852607 0.31343018
0.36082217 0.4449084 0.11814833 0.89293472 0.48887375 0.33682473
0.50663072 0.99573468 0.56172571 0.67126407 0.82313645 0.30861287
0.83140746 0.05285592 0.52025646 0.97192002 0.69488506 0.26584835
0.71075032 0.31535233 0.97442643 0.90242584 0.87177382 0.60438133
0.45030455 0.70864482 0.57518814 0.09044136 0.74346058 0.10024626
0.0408114 0.13287688 0.85784692 0.03787268 0.51931731 0.20832441
0.3880822 0.50524611 0.04926207 0.8398687 0.49066355 0.29365035
0.31442561 0.63639672 0.56949927 0.62473007 0.41733016 0.6282564
0.31666614 0.45719453 0.05920186 0.28278621 0.21508996 0.52478958
0.19995624 0.21906851 0.01380596 0.86616696 0.03639796 0.88335764
0.27265405 0.98767091 0.86073049 0.7010772 0.01781981 0.25839967
0.25399892 0.11907349 0.70671217 0.91646761 0.12017356 0.95450994
0.29517175 0.27535272 0.36116569 0.77153018 0.3022805 0.32689434
0.75088046 0.36458859 0.78798403 0.93310726]
粗略检验通过,进行频率检验
对于(0,1)均匀分布数分成n组\(\left(0, \quad \frac{1}{n}\right),\left(\frac{1}{n}, \frac{2}{n}\right), \cdots\left(\frac{n-1}{n}, 1\right)\),每组的理论频数\(E_{i}=\frac{N}{n}\),\(N\)为随机数个数,实际频数为\(Q_i\),统计量\(\bar{c}=\sum_{i=1}^{n} \frac{\left(Q_{i}-E_{i}\right)^{2}}{E_{i}^{2}}\)服从\(\chi_{n-1}^2\)分布,对于一定数量\(\frac{N}{n}\geqslant5\),若采用5%的置信度,查\(\chi_{n-1}^2\)分布表,得\(\chi_{0.05(n-1)}^2\),若\(\bar{c}<\chi_{0.05(n-1)}^2\),认为这批随机数在统计性能上是95%可信。
if frequency_test(randow_num_list):
print("频率检验通过!")
else:
print("频率检验失败!")
输出结果:
频率检验通过!
独立性检验--相关系数检验
给定\(N\)个服从相同分布的随机数\(r_1,r_2,\dots,r_n\),我们计算前后距离为\(j\)的两个随机样本的相关系数\(R_j\)
R = corr_coeffient_test(randow_num_list, 1)
print("距离为1的相关系数为:", R)
R = corr_coeffient_test(randow_num_list)
print("距离为5的相关系数为:", R)
R = corr_coeffient_test(randow_num_list, 10)
print("距离为10的相关系数为:", R)
R = corr_coeffient_test(randow_num_list, 20)
print("距离为20的相关系数为:", R)
R = corr_coeffient_test(randow_num_list, 50)
print("距离为50的相关系数为:", R)
输出结果:
距离为1的相关系数为: -1.0571511721357674
距离为5的相关系数为: -2.2119618825288287
距离为10的相关系数为: -1.1470855033688878
距离为20的相关系数为: -0.9568683998367279
距离为50的相关系数为: 0.4553730525624434
独立性检验--联立表检验
if simu_table_test(randow_num_list):
print("这100个随机数在独立性上95%是可信的!")
else:
print("没有把握确定这100个随机数在独立性上95%是可信的!")
输出结果:
这100个随机数在独立性上95%是可信的!
舍选法生成100个随机数并进行效率求解
num = 100#舍选法随机数的个数
objection = rejection_method(randow_num_list, num)
print("生成的",num,"个服从要求密度函数的随机数列为:\n", objection['obje_randow_list'])
print("理论效率为:", objection['theory_efficience'])
print("仿真效率为:", objection['emulational_efficience'])
输出结果:
生成的 100 个服从要求密度函数的随机数列为:
[0.85159487 0.38553153 0.09123632 0.80387689 0.76666027 0.18396305
0.75009426 0.5288669 0.11249721 0.23132686 0.37451616 0.54591484
0.46852607 0.31343018 0.36082217 0.4449084 0.11814833 0.89293472
0.33682473 0.50663072 0.56172571 0.67126407 0.82313645 0.30861287
0.83140746 0.05285592 0.52025646 0.97192002 0.26584835 0.31535233
0.97442643 0.87177382 0.60438133 0.45030455 0.70864482 0.57518814
0.09044136 0.74346058 0.10024626 0.0408114 0.13287688 0.85784692
0.03787268 0.51931731 0.20832441 0.3880822 0.50524611 0.04926207
0.8398687 0.49066355 0.29365035 0.31442561 0.63639672 0.56949927
0.62473007 0.41733016 0.6282564 0.31666614 0.45719453 0.05920186
0.28278621 0.21508996 0.19995624 0.21906851 0.01380596 0.86616696
0.03639796 0.88335764 0.27265405 0.7010772 0.01781981 0.25839967
0.25399892 0.11907349 0.70671217 0.12017356 0.29517175 0.27535272
0.36116569 0.3022805 0.32689434 0.75088046 0.78798403 0.93310726
0.85159487 0.38553153 0.09123632 0.80387689 0.66494775 0.86175315
0.74260715 0.99250419 0.76666027 0.18396305 0.75009426 0.5288669
0.11249721 0.37451616 0.54591484 0.46852607]
理论效率为: 0.8722740982016987
仿真效率为: 0.8547008547008547
查看舍选法生成随机数的拟合效果
randow_num_list_test=avg_random(100000)
obje_randow_list_test=rejection_method(randow_num_list_test, 10000)['obje_randow_list']
bins = np.arange(0, 1.1,0.1)
weights = np.ones_like(obje_randow_list_test) / len(obje_randow_list_test)
plt.hist(obje_randow_list_test, weights=weights, bins=bins)
samples = np.arange(0.05,1,0.1)
density = fuc(samples)
density_1 = density / sum(density)
plt.plot(samples, density_1)
plt.title('概率密度函数拟合图')
plt.show()
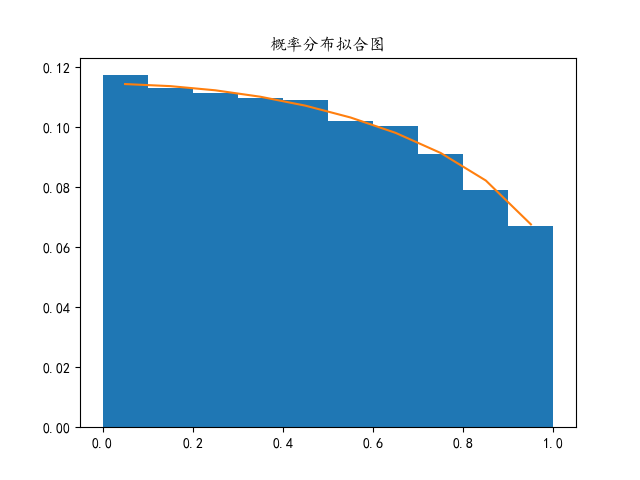
概率分布拟合图


 浙公网安备 33010602011771号
浙公网安备 33010602011771号