cdoj913-握手 【Havel定理】

http://acm.uestc.edu.cn/#/problem/show/913

握手

Time Limit: 2000/1000MS (Java/Others)     Memory Limit: 65535/65535KB (Java/Others)

Submit Status

一群人参加了一次聚会，其中有一些人是好朋友。一对朋友见面后握手且仅握一次手，并且每个人不会和自己握手（废话！）。现在告诉你每个人一共握了几次手，请你判断是否存在一种朋友关系满足每个人的握手数。

Input

输入多组数据，第一行一个数T，表述数据组数。每组数据第一行输入一个数n，表示有n个人参加了聚会，下一行有n个数，di到dn ，di表示第i个人的握手数。 （1≤n≤105 ，输入的所有d之和不超过5×105）

Output

存在这种朋友关系输出YES，反之NO。

Sample input and output

Sample Input	Sample Output
3 3 0 1 1 3 2 2 2 3 1 1 1	YES YES NO

 

 

 

题解：用Havel定理解即可。

握手定理：任意图所有顶点度数之和必为偶数。

度序列：V(G)={v1,v2,....vn},称序列 {d(v1),d(v2),....d(vn)}为度序列。

一个正整数序列(d1,d2,.....,dn)是度序列当且仅当。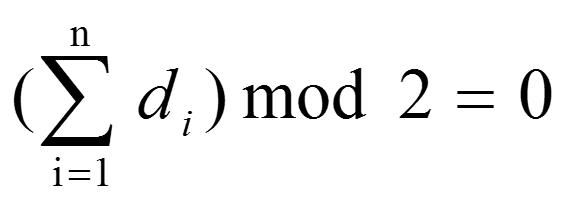

Havel定理：

一个序列：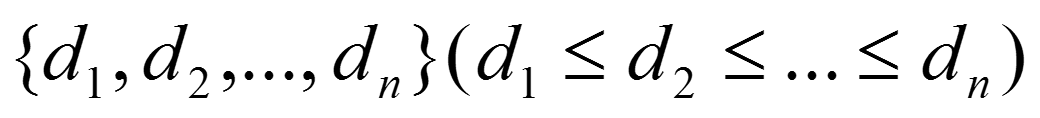

是简单图的度序列当且仅当：

算法流程：

设序列有n个元素，d1,d2,....dn

1、若序列中出现负数则无解，若序列全为为0则有解，否则转2。

2、取出序列中最大值dmax，若dmax大于n-1,无解退出。否则取出剩下n-1个元素中前dmax大的dmax个元素，把这些元素依次减1后放回序列中，dmax舍弃，n=n-1。

代码：

#include <fstream>
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>

using namespace std;

const int N=100005;
priority_queue<int> p;
int n;
int a[N],t[N];
bool b;

int main()
{
    //freopen("D:\\input.in","r",stdin);
    //freopen("D:\\output.out","w",stdout);
    int T,cnt;
    scanf("%d",&T);
    while(T--){
        cnt=0;
        b=1;
        scanf("%d",&n);
        for(int i=0;i<n;i++){
            scanf("%d",&a[i]);
            cnt+=a[i];
        }
        if(cnt&1)   puts("NO");
        else{
            while(!p.empty())   p.pop();
            for(int i=0;i<n;i++)    p.push(a[i]);
            while(!p.empty()){
                cnt=p.top();
                p.pop();
                if(cnt>=n){
                    b=0;
                    break;
                }else if(cnt==0){
                    break;
                }
                if(p.size()<cnt){
                    b=0;
                    break;
                }else{
                    for(int i=0;i<cnt;i++){
                        t[i]=p.top()-1;
                        p.pop();
                    }
                    if(t[cnt-1]<0){
                        b=0;
                        break;
                    }
                    for(int i=0;i<cnt;i++)
                        if(t[i])    p.push(t[i]);
                    n--;
                }
            }
            if(b)   puts("YES");
            else    puts("NO");
        }
    }
    return 0;
}