【算法】树状数组

在前面的文章我提到过，如果想要多次求和，可以使用前缀和，通过预处理的手法，可以使得求和的复杂度是O(1)。
但是，如果我们把题目改一下：

现在有一些操作：
操作A 输入1 L R，输出L-R区间的和
操作B 输入2 P X，使得A[P]+=X

A[P]+=X就是对A数组进行修改。
如果使用前缀和，求和的复杂度是O(1)没错，但是修改时候，要把所有的后面的前缀和也要修改，修改复杂度变成了O(n)
而使用普通的模拟算法，修改的复杂度是O(1)，但是求和的复杂度是O(n)，因为要使用for循环从L加到R

有没有更好的算法，使得修改的复杂度和求和的复杂度尽可能小？

首先明确一点，两个全部是O(1)是不可能的。所以，我们把目光转向O(log n)，是否可能？
答案是肯定的。
假设我们要求A[1...11]的和， 那么，我们将它拆分成：

A[1...8]+A[9...10]+A[11]

容易看出，11=8+2+1，因此我们这样拆分。

同理，求A[1...80]，我们可以这样拆分：

A[1..64]+A[65..80] //80=64+16

如果是求A[L...R]，可以通过A[1...R]-A[1..L-1]做减法。
容易看出，我们是通过二进制的位来拆分的。
使用C数组来预处理，那么对应的关系就是：

a[1]		c[1]
a[1..2]		c[2]
a[1..3]		c[1]+a[3] /*c[3]=a[3]*/
a[1..4]		c[4]
a[1..5]		c[4]+a[5] /*c[5]=a[5]*/
a[1..6]		c[4]+a[5..6] /*c[6]=a[5..6]*/

任意一个段的和，必然是通过这些数字相加的。
如果文字不直观，我们看图，就非常直观了：

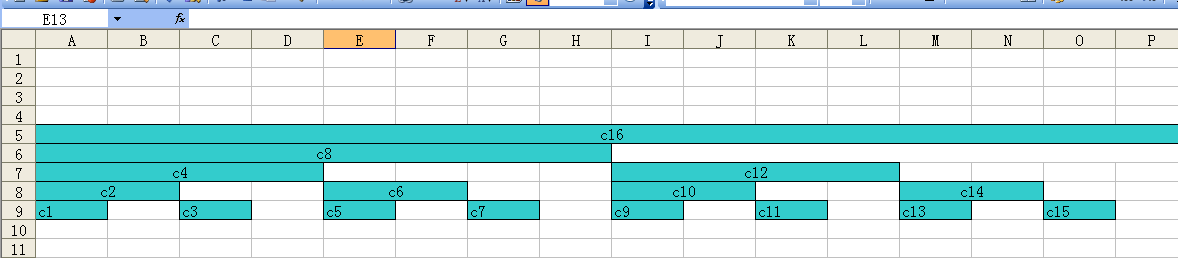
这就是树状数组。

1.lowbit
首先我们需要对数字进行拆分。例如12=8+4,11=8+4+1
容易看出，这些要拆分的数，就是它们二进制的最后一位
我们可以写一个叫做lowbit的函数获取最后一位，这个算法很精妙。

int lowbit(int x){
  return x&(-x);
}

2.求和
求出A[1..Pos]的和，我们可以不断寻找他们的lowbit并找出对应的数相加
我们先举例：A[1...11]

黄色部分就是要相加的数。

int getsum(int pos){	//求出a[1..pos]
    int res=0;
    for(int i=pos;i>0;i-=lowbit(i)){
        res+=c[i];
    }
    return res;
}

3.更新
如果我们需要修改c5+=x，那么， 看图，需要修改的部分就是：

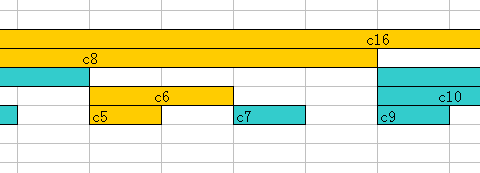
就是它上方的区域，同样可以使用lowbit解决。
void update(int i,int x){ // a[i]+=x
for(int j=i;j<=n;j+=lowbit(j))c[j]+=x;
}

4.总结
我们可以看到，所有需要使用到的操作，都是O(log n)复杂度的。

5.题目

模板题

#include<bits/stdc++.h>
using namespace std;
int n,k;
const int N=5e5+10;
int c[N];
int lowbit(int x){
	return x&(-x);
}
int getsum(int pos){	//求出a[1..pos]
    int res=0;
    for(int i=pos;i>0;i-=lowbit(i)){
        res+=c[i];
	}
    return res;
}
void update(int i,int x){ 			// a[i]+=x
    for(int j=i;j<=n;j+=lowbit(j))c[j]+=x;
}
int main(){
	scanf("%d%d",&n,&k);
	while(k--){
		char c[2];
		int m,p;
		scanf("%s",c);
		if(c[0]=='A'){
			scanf("%d",&m); 
			printf("%d\n",getsum(m));
		}
		else if(c[0]=='B'){
			scanf("%d%d",&m,&p);
			update(m,p);
		}
		else if(c[0]=='C'){
			scanf("%d%d",&m,&p);
			update(m,-p);
		}
		
	}
	return 0;
}