数据结构之堆排序

• 基本思想

       对于给定的n个记录，初始时把这些记录看做一颗顺序存储的二叉树，然后将其调整为一个大顶堆，然后将堆的最后一个元素与对顶元素进行交换后，堆的最后一个元素即为最大记录；接着将前(n-1)个元素重新调整为一个大顶堆，再将堆顶元素与当前堆的最后一个元素进行交换后得到次大的记录，重复该过程知道调整的堆中只剩一个元素时为止，该元素即为最小记录，此时可得到一个有序序列。

 

• 堆排序过程

1. 构建堆
2. 交换堆顶元素与最后一个元素的位置

 

• 堆排序示例图

       给定一个整形数组a[]={16,7,3,20,17,8}，对其进行堆排序。 首先根据该数组元素构建一个完全二叉树，得到

       然后需要构造初始堆，则从最后一个非叶节点开始调整，调整过程如下：

      20和16交换后导致16不满足堆的性质，因此需重新调整

      这样就得到了初始堆。

      先进行一次调整时其成为大顶堆，即每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质，因此每次交换之后要重新对被交换的孩子节点进行调整)。有了初始堆之后就可以进行排序了。

       此时3位于堆顶不满堆的性质，则需调整继续调整。

  

         这样整个区间便已经有序了！！！

 

• 程序如下

import java.util.*;
public class test {

    public static void main(String[] args) {  
        int[] data5 = new int[] { 5, 3, 6, 2, 1, 9, 4, 8, 7 };  
        print(data5);  
        heapSort(data5);  
        System.out.println("排序后的数组：");  
        print(data5);  
    }  
  
    public static void swap(int[] data, int i, int j) {  
        if (i == j) {  
            return;  
        }  
        data[i] = data[i] + data[j];  
        data[j] = data[i] - data[j];  
        data[i] = data[i] - data[j];  
    }  
  
    public static void heapSort(int[] data) {  
        for (int i = 0; i < data.length; i++) {  
            createMaxdHeap(data, data.length - 1 - i);  
            swap(data, 0, data.length - 1 - i);  
            print(data);  
        }  
    }  
  
    public static void createMaxdHeap(int[] data, int lastIndex) {  
        for (int i = (lastIndex - 1) / 2; i >= 0; i--) {  
            // 保存当前正在判断的节点  
            int k = i;  
            // 若当前节点的子节点存在  
            while (2 * k + 1 <= lastIndex) {  
                // biggerIndex总是记录较大节点的值,先赋值为当前判断节点的左子节点  
                int biggerIndex = 2 * k + 1;  
                if (biggerIndex < lastIndex) {  
                    // 若右子节点存在，否则此时biggerIndex应该等于 lastIndex  
                    if (data[biggerIndex] < data[biggerIndex + 1]) {  
                        // 若右子节点值比左子节点值大，则biggerIndex记录的是右子节点的值  
                        biggerIndex++;  
                    }  
                }  
                if (data[k] < data[biggerIndex]) {  
                    // 若当前节点值比子节点最大值小，则交换2者得值，交换后将biggerIndex值赋值给k  
                    swap(data, k, biggerIndex);  
                    k = biggerIndex;  
                } else {  
                    break;  
                }  
            }  
        }  
    }  
  
    public static void print(int[] data) {  
        for (int i = 0; i < data.length; i++) {  
            System.out.print(data[i] + "\t");  
        }  
        System.out.println();  
    }  

}

     程序结果

 

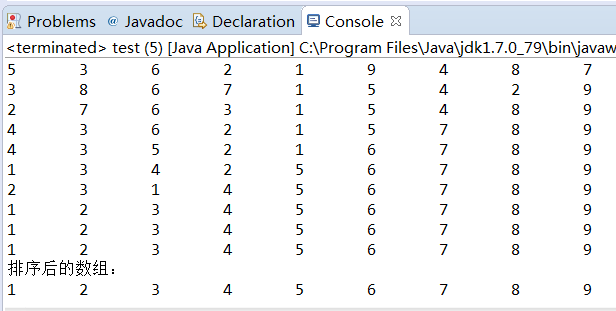
• 算法分析

1. 最好时间：O(nlogn)
2. 平均时间：O(nlogn)
3. 最坏时间：O(nlogn)
4. 辅助存储：O(1)
5. 稳定性：不稳定

 

文章参考：http://lib.csdn.net/article/datastructure/8973

             http://blog.csdn.net/apei830/article/details/6584645