| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
|---|---|
| 这个作业的地址 | DS博客作业04--图 |
| 这个作业的目标 | 学习图结构设计及相关算法 |
| 姓名 | 郑俊佳 |
0.PTA得分截图
1.本周学习总结（6分）
本次所有总结内容，请务必自己造一个图（不在教材或PPT出现的图），围绕这个图展开分析。建议：Python画图展示。图的结构尽量复杂，以便后续可以做最短路径、最小生成树的分析。
1.1 图的存储结构
1.1.1 邻接矩阵（不用PPT上的图）
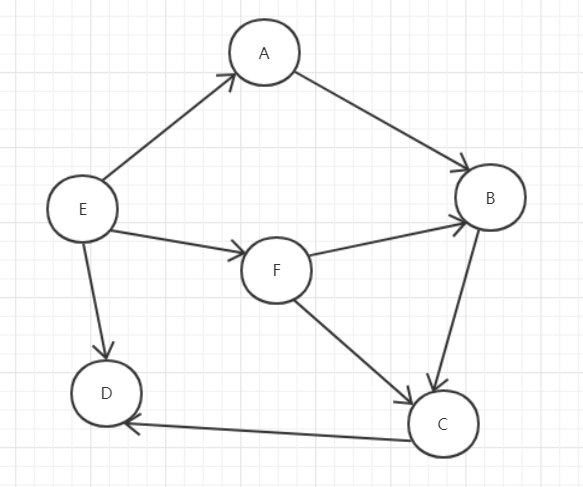
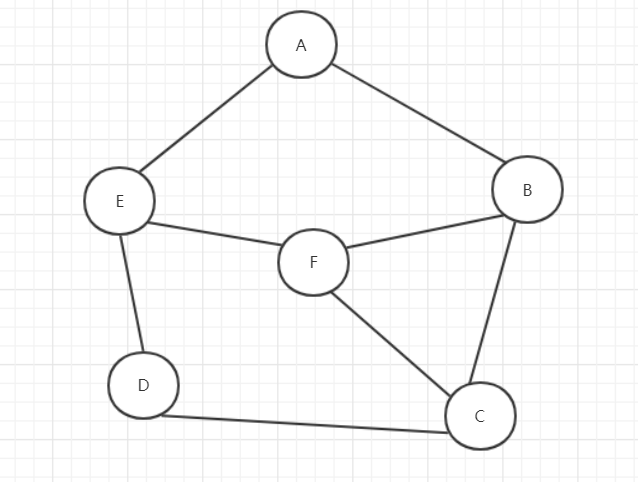
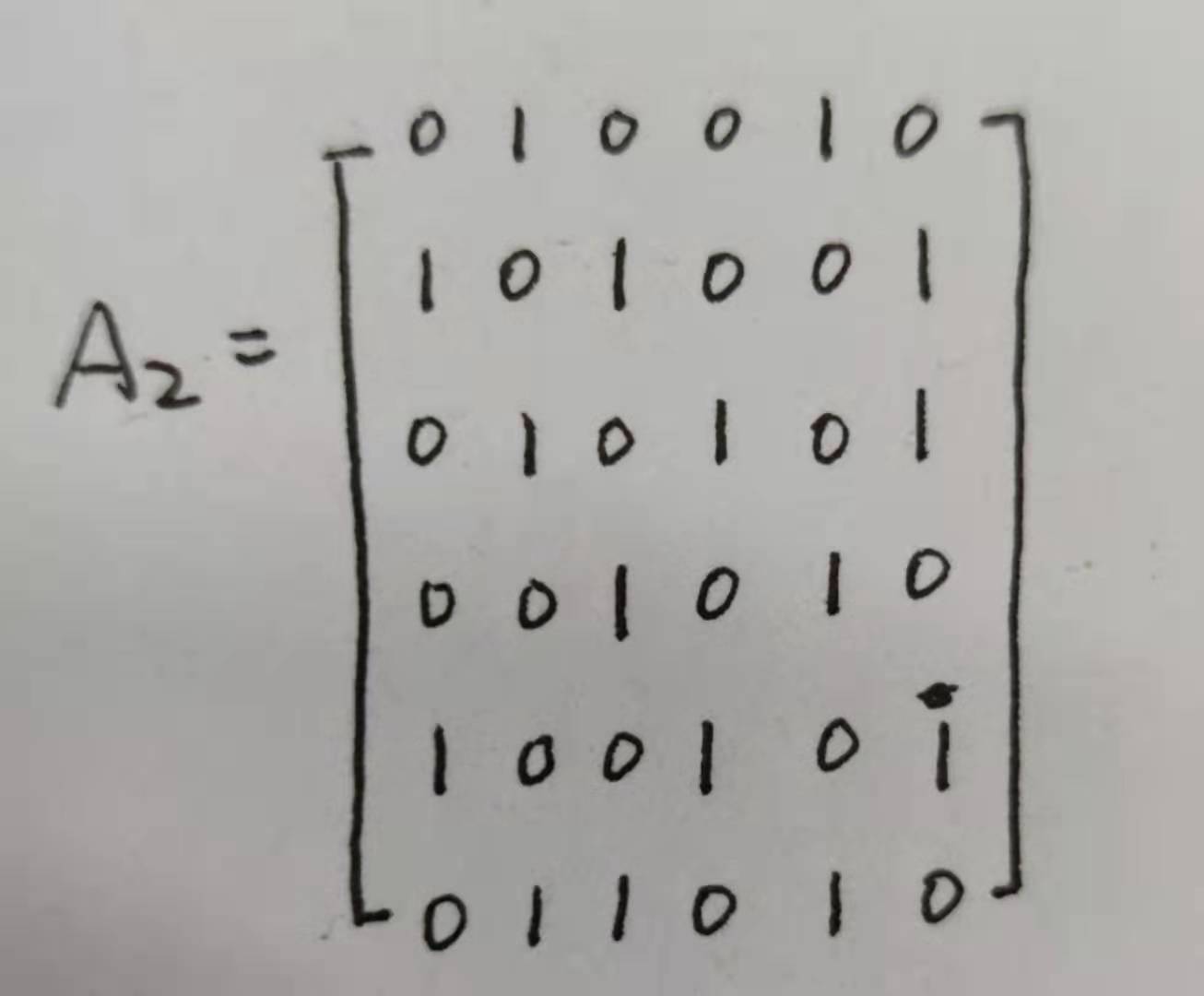
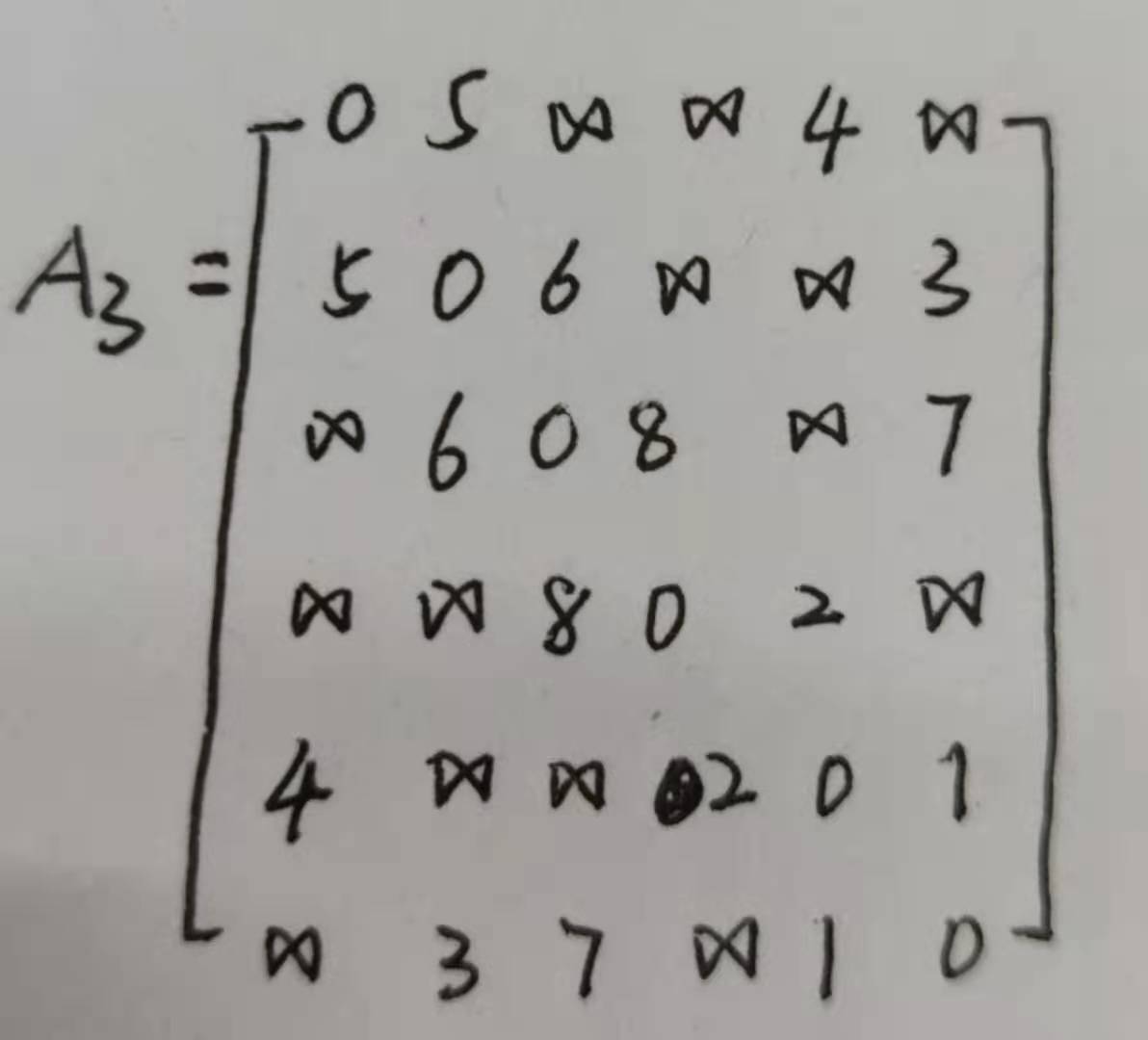
邻接矩阵的结构体定义
#define MAXV<最大顶点个数>
#define INF 32767 //定义无穷大
typedef struct
{
int no; //顶点的编号
infoType info; //顶点的其他信息
}VertexType; //顶点的类型
typedef struct
{
int edges[MAXV][MAXV]; //邻接矩阵数组
int n,e; //顶点数，边数
VertexType vexs[MAXV]; //存放顶点信息
}MatGraph; //完整的图邻接矩阵类型
建图函数
1.1.2 邻接表
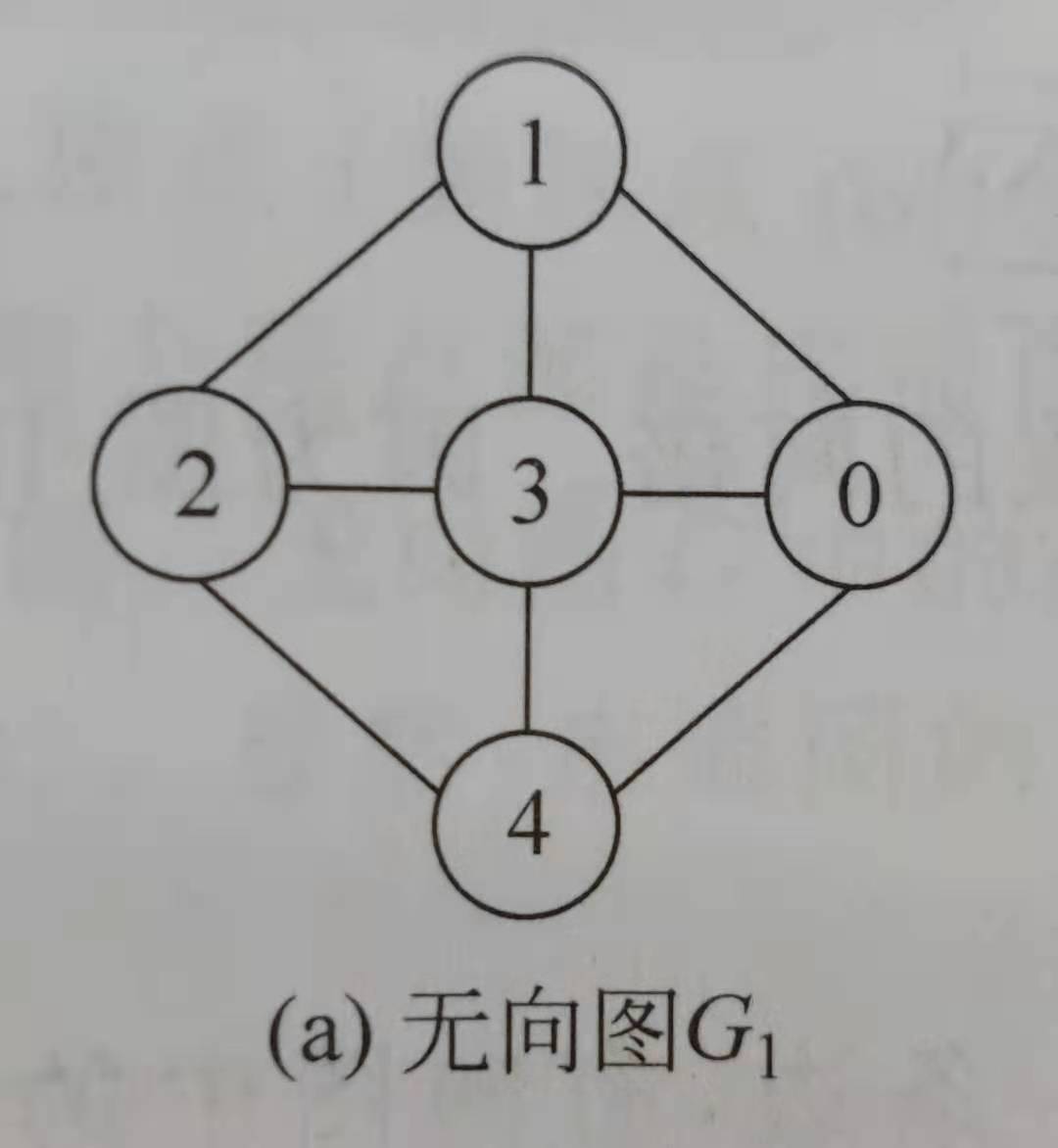
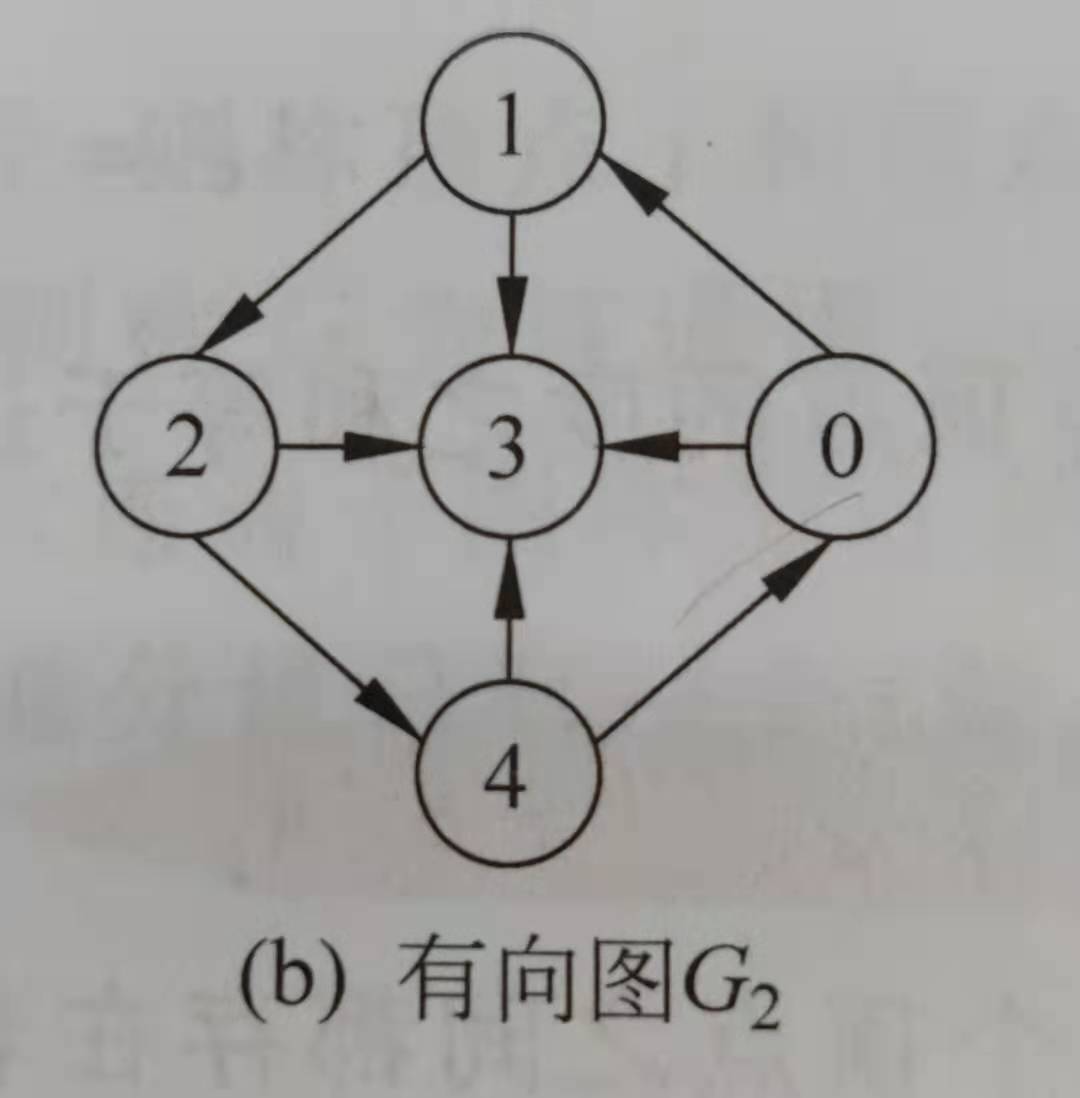
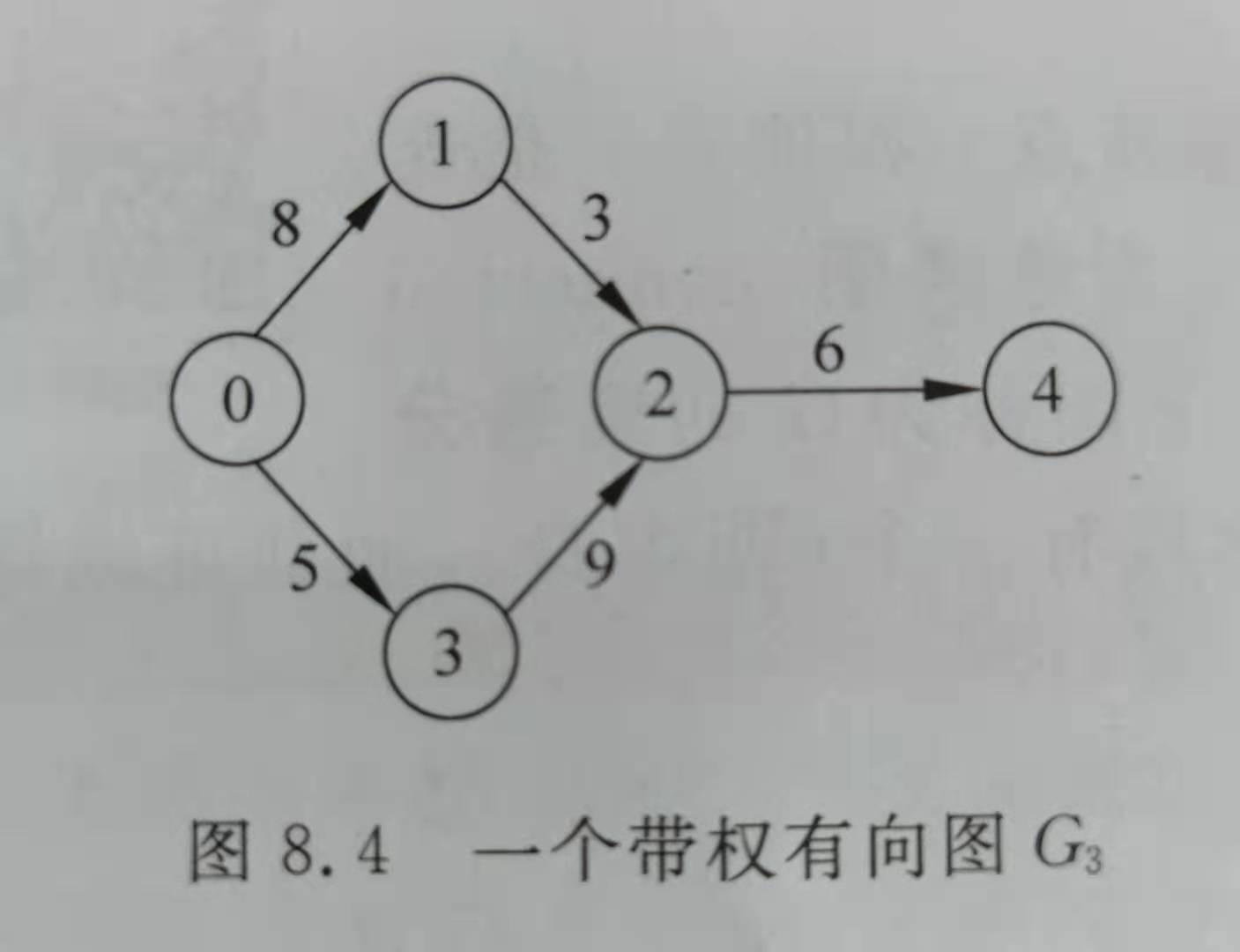
邻接矩阵的结构体定义
typedef struct ANode
{
int adjvex; //该边的邻接点编号
struct ANode * nextarc; //指向下一条边的指针
int weight; //该边的相关信息，如权值（这里用整型表示）
}ArcNode; //边结点的类型
typedef struct Vnode
{
InfoType info; //顶点的其他信息
ArcNode * firstarc; //指向第一个边结点
}VNode; //邻接表的头结点类型
typedef struct
{
VNode adjlist[MAXV]; //邻接表的头结点数组
int n,e; //图中的顶点数n和边数e
}AdjGraph; //完整的图邻接表类型
建图函数
1.1.3 邻接矩阵和邻接表表示图的区别
邻接矩阵适合用于稠密图，而邻接表更适合用于稀疏图。
邻接矩阵时间复杂度为O(n2<\sup>),n为顶点个数。
邻接表时间复杂度为O(n+e），n为顶点个数，e为边数。
1.2 图遍历
1.2.1 深度优先遍历
选上述的图，继续介绍深度优先遍历结果
深度遍历代码
int visited[MAX]={0}; //全局数组
void DFS(AdjGraph *G,int v) //深度优先遍历算法
{
ArcNode * p;
visited[v]=1; //置已访问标记
printf("%d",v); //输出被访问顶点的编号
p=G->adjlist[v].firstarc; //p指向顶点v的第一个邻接点
while(p!=NULL)
{
if(visited[p->adjvex]==0) //若p->adjvex顶点未被访问，递归访问它
DFS(G,p->adjvex);
p=p->nextarc; //p指向顶点v的下一个邻接点
}
}
适用于解决：求无向图的连通分量的个数、连通分量都包含哪些顶点、两个顶点是否在同一个连通分量中、单源路径问题、检测无向图中的环、二分图检测等等
引用一篇博客：深度优先遍历的应用
1.2.2 广度优先遍历
选上述的图，继续介绍广度优先遍历结果
广度遍历代码
void BFS(AdjGraph * G,int v)
{
int w,i;
ArcNode * p;
SqQueue * qu;
InitQueue(qu);
int visited[MAXV];
for (i=0;i<G->n;i++）
visited[i]=0;
printf("%2d",v);
visited[v]=1;
enQueue(qu,v);
while(!QueueEmpty(qu))
{
deQueue(qu,w);
p=G->adjlist[w].firstarc;
while(p!=NULL)
{
if(visited[p->adjvex]==0)
{
printf("%2d",p->adjvex);
visited[p->adjvex]=1;
enQueue(qu,p->adjvex);
}
p=p->nextarc;
}
}
printf("\n");
}
适用于解决：求解单源路径问题、求解联通分量的个数、具体的每一个连通分量都包含哪些顶点、环检测、二分图的检测等等
引用一篇博客：广度优先遍历的应用
1.3 最小生成树
最小生成树是一条最短路径（包含所有顶点的路径），所有路径的权值相加最小，且边最少即为n-1（n为顶点数）；
1.3.1 Prim算法求最小生成树
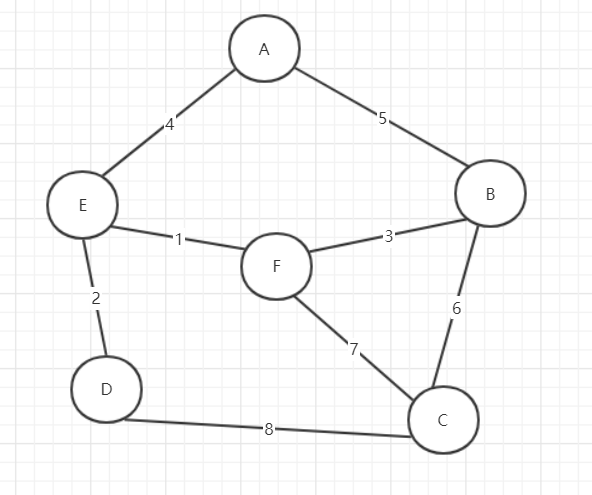
基于上述图结构求Prim算法生成的最小生成树的边序列
Prim算法的两个辅助数组是：closest和lowcost。
对于V-U中的一个顶点j，它的最小边对应U中的某个顶点，则用closest[j]保存U中的这个顶点。并用lowcost[j]保存该最小边所对应的权值。
void Prim(MatGraph g,int v)
{
int lowcost[MAXV];
int MIN;
int closest[MAXV],i,j,k;
for(i=0;i<g.n;i++) //给lowcost[]、closest[]置初值
{
lowcost[i]=g.edges[v][i];
closest[i]=v;
}
for(i=1;i<g.n;i++) //找出（n-1）个顶点
{
MIN=INF;
for(j=0;j<g.n;j++) //在（V-U）中找出离U最近的顶点k
if(lowcost[j]!=0&&lowcost[j]<MIN)
{
MIN=lowcost[j];
k=j; //k记录最近顶点的编号
}
printf("边(%d,%d)权为:%d\n",closest[k],k,MIN); //输出最小生成树的一条边
lowcost[k]=0; //标记k已经加入U
for(j=0;j<g.n;j++) //对（V-U）中的顶点j进行调整
if(lowcost[j]!=0&&g.wdges[k][j]<lowcost[j])
{
lowcost[j]=g.edges[k][j];
closest[j]=k; //修改数组lowcost和closest
}
}
}
Prim算法的时间复杂度是：O（n2）
Prim算法适用于稠密图，可以不用判断是否产生回路，因为在待选边表中不停计算的过程中，可以有效避免产生回路的情况。其时间复杂度只与节点数量有关，在特定情况下可以更快的执行完程序。
1.3.2 Kruskal算法求解最小生成树
基于上述图结构求Kruskal算法生成的最小生成树的边序列
实现Kruskal算法的辅助数据结构是什么？其作用是什么？Kruskal算法代码。
实现Kruskal算法的辅助数据结构是一个辅助数组vset[0...(n-1)]，用于记录一个顶点i所在的连通分量编号，即vset[i];
其辅助数组用于判断选取的一条边会不会使其最小生成树出现回路。
typedef struct
{
int u; //边的起始顶点
int v; //边的终止顶点
int w; //边的权值
}Edge;
void Kruskal(MatGraph g) //Kruskal算法
{
int i,j,u1,v1,sn1,sn2,k;
int vset[MAXV];
Edge E[MaxSize]; //存放图中的所有边
k=0; //e数组的下标从0开始计
for(i=0;i<g.n;i++) //由g产生边集E，不重复选取同一条边
for(j=0;j<=i;j++)
if(g.edges[i][j]!=0&&g.edges[i][j]!=INF)
{
E[k].u=i;
E[k].v=j;
E[k].w=g.edges[i][j];
k++;
}
InsertSort(E,g.e); //采用直接插入排序对E数组按权值递增排序
for(i=0;i<g.n;i++) //初始化辅助数组
vset[i]=i;
k=1; //k表示当前构造生成树的第几条边，初值为1
j=0; //E中边的下标，初值为0
while(k<g.n) //生成的边数小于n时循环
{
u1=E[j].u;v1=E[j].v; //取一条边的两个顶点
sn1=vset[u1];
sn2=vset[v1]; //分别得到两个顶点所属的集合编号
if(sn1!=sn2) //两顶点属于不同的集合，该边是最小生成树的一条边
{
printf("(%d,%d):%d\n",u1,v1,E[j].w); //输出最小生成树的一条边
k++; //生成边数增1
for(i=0;i<g.n;i++) //两个集合统一编号
if(vest[i]==sn2) //集合编号为sn2的改为sn1
vset[i]=sn1;
}
j++; //扫描下一条边
}
}
void Kruskal(MatGraph g) //改进的Kruskal算法
{
int i,j,k,u1,v1,sn1,sn2;
UFSTree t[MaxSize];
Edge E[MaxSize];
k=1; //e数组的下标从1开始计
for(i=0;i<g.n;i++) //由g产生的边集E
for(j=0;j<=i;j++)
if(g.edges[i][j]!=0&&g.edges[i][j]!=INF)
{
E[k].u=i;
E[k].v=j;
E[k].w=g.edges[i][j];
}
HeapSort(E,g.e); //采用堆排序对E数组按权值递增排序
MAKE_SET(t,g.n); //初始化并查集树t
k=1; //k表示当前构造生成树的第几条边，初值为1
j=1; //E中边的下标从1开始
while(k<g.n) //生成的边数小于n时循环
{
u1=E[j].u;
v1=E[j].v; //取一条边的头尾顶点编号u1和v2
sn1=FIND_SET(t,u1);
sn2=FIND_SET(t,v1); //分别得到两个顶点所属的集合编号
if(sn1!=sn2) //两顶点属于不同的集合，该边是最小生成树的一条边
{
printf("(%d,%d):%d\n",u1,v1,E[j].w);
k++; //生成边数增1
UNION(t,u1,v1); //将u1和v1两个顶点合并
}
j++; //扫描下一条边
}
}
未改进前Kruskal算法的时间复杂度是O(e2)
改进后Kruskal算法的时间复杂度是O(elog2e)
Kruskal算法适用于求稀疏图中的最小生成树,不需要用邻接表或者邻接矩阵存图，只需要用个结构体存边即可。其思路比Prim算法清晰很多。
1.4 最短路径
1.4.1 Dijkstra算法求解最短路径
Dijkstra算法需要两个辅助数组dist[MAXV], path[MAXV]，前者用于存储各点到所求点的最短路程，后者用于存储其他的点到所求点路径的上一点。
void Dijkstra(MatGraph g,int v) //Dijkstra算法
{
int dist[MAXV],path[MAXV];
int S[MAXV]; //S[i]=1表示顶点i在S中，S[i]=0表示顶点i在U中
int MINdis,i,j,u;
for(i=0;i<g.n;i++)
{
dist[i]=g.edges[v][i]; //距离初始化
S[i]=0; //S[]置空
if(g.edges[v][i]<INF) //路径初始化
path[i]=v; //顶点v到顶点i有边时，置顶点i的前一个顶点为v
else
path[i]=-1; //顶点v到顶点i没有边时，置顶点i的前一个顶点为-1
}
S[v]=1; //源点编号v放入S中
path[v]=0;
for(i=0;i<g.n-1;i++) //循环直到所有顶点的最短路径都求出
{
MINdis=INF; //MINdis置最大长度初值
for(j=0;j<g.n;j++) //选取不在S中（即U中）且具有最小最短路径长度的顶点u
if(S[j]==0&&dist[j]<MINdis)
{
u=j;
MINdis=dist[j];
}
S[u]=1; //顶点u加入S中
for(j=0;j<g.n;j++) //修改不在S中（即U中）的顶点的最短路径
if(S[j]==0)
if(g.edges[u][j]<INF&&dist[u]+g.edges[u][j]<dist[j])
{
dist[j]=dist[u]+g.edges[u][j];
path[j]=u;
}
}
Dispath(g,dist,path,S,v); //输出最短路径
}
void Dispath(MatGraph g,int dist[],int path[],int S[],int v)
{
int i,j,k;
int apath[MAXV],d; //存放一条最短路径（逆向）及其顶点个数
for(i=0;i<g.n;i++) //循环输出从顶点v到i的路径
if(S[i]==1&&i!=v)
{
printf("从顶点%d到顶点%d的路径长度为：%d\t路径为:",v,i,dist[i]);
d=0; //添加路径上的终点
apath[d]=i;
k=path[i];
if(k==-1) //没有路径的情况
printf("无路径\n");
else //存在路径时输出该路径
{
while(k!=v)
{
d++;
apath[d]=k;
k=path[k];
}
d++; //添加路径上的起点
apath[d]=v;
printf("%d",apath[d]); //先输出起点
for(j=d-1;j>=0;j--) //再输出其他顶点
printf(",%d",apath[j]);
printf("\n");
}
}
}
Dijkstra算法的时间复杂度为O(n2)，适用于有权图，并要求其权不为负的。
因为dijkstra是基于贪心策略，每次都找一个距源点最近的点，然后将该距离定为这个点到源点的最短路径；
但如果存在负权边，那就有可能先通过并不是距源点最近的一个次优点，再通过这个负权边，使得路径之和更小，这样就出现了错误。
例题：
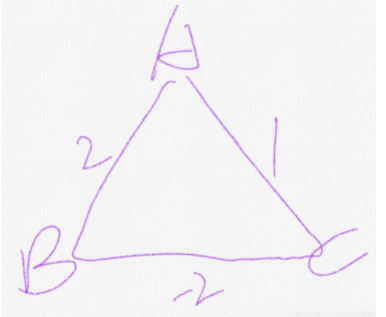
对于上图将A添加到集合中标记已访问，之后选出从A到所有节点中的最短的点，于是把C加入集合中标记已访问，之后C不能在更新了。
而显然，A与C之间最短路径权值为0（A-B-C），发生错误。
1.4.2 Floyd算法求解最短路径
Floyd算法解决求每一个顶点到其他顶点的最短路径问题。
Floyd算法使用邻接矩阵来存储图结构，需要以下两个辅助数据结构：
1.二维数组 Path[i][j]：最短路径上顶点 vj 的前一顶点的序号；
2.二维数组 A[i][j]：记录顶点 vi 和 vj 之间的最短路径长度；
void Floyd(MatGraph g) //Floyd算法
{
int A[MAXV][MAXV],path[MAXV][MAXV];
int i,j,k;
for(i=0;i<g.n;i++)
for(j=0;j<g.n;j++)
{
A[i][j]=g.edges[i][j];
if(i!=j&&g.edges[i][j]<INF)
path[i][j]=i; //顶点i到j有边时
else
path[i][j]=-1; //顶点i到j没有边时
}
for(k=0;k<g.n;k++) //依次考查所有顶点
{
for(i=0;i<g.n;i++)
for(j=0;j<g.n;j++)
if(A[i][j]>A[i][k]+A[k][j])
{
A[i][j]=A[i][k]+A[k][j]; //修改最短路径长度
path[i][j]=path[k][j]; //修改最短路径
}
}
Dispath(g,A,path); //输出最短路径
}
void Dispath(MatGraph g,int A[][MAXV],int path[][MAXV])
{
int i,j,k,s;
int apath[MAXV],d; //存放一条最短路径中间顶点（反向）及其顶点个数
for(i=0;i<g.n;i++)
for(j=0;j<g.n;j++)
{
if(A[i][j]!=INF&&i!=j) //若顶点i和j之间存在路径
{
printf("从%d到%d的路径为:",i,j);
k=path[i][j];
d=0; //路径上添加终点
apath[d]=j;
while(k!=-1&&k!=i) //路径上添加中间点
{
d++;
apath[d]=k;
k=path[i][k];
}
d++; //路径上添加起点
apath[d]=i;
printf("%d",apath[d]); //输出起点
for(s=d-1;s>=0;s--) //输出路径上中间顶点
printf(",%d",apath[s]);
printf("\t路径长度为:%d\n",A[i][j]);
}
}
}
Floyd算法是一种动态规划算法，稠密图效果最佳，边权可正可负。
此算法简单有效，由于三重循环结构紧凑，对于稠密图，效率要高于执行|V|次Dijkstra算法，也要高于执行V次SPFA算法。
优缺点如下：
优点：容易理解，可以算出任意两个节点之间的最短距离，代码编写简单。
缺点：时间复杂度为O(n3)比较高，不适合计算大量数据。
1.5 拓扑排序
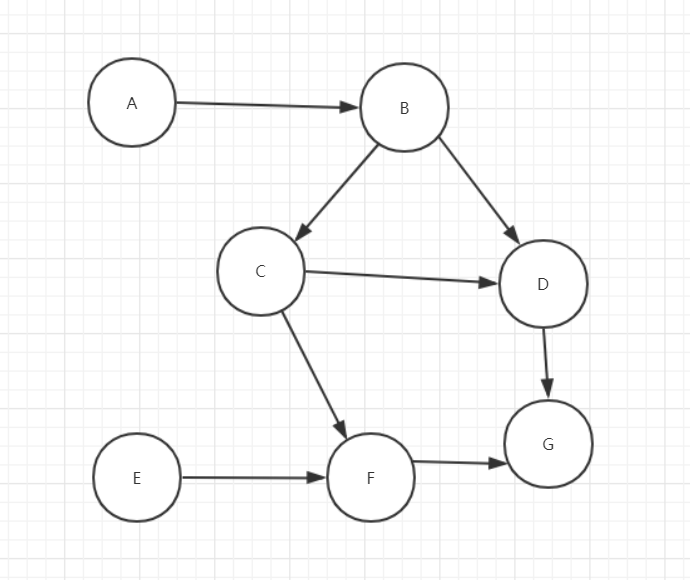
上有向图的一种拓扑序列A->E->B->C->F->D->G
实现拓扑排序代码，结构体如何设计？
typedef struct
{
Vertex data; //顶点信息
int count; //增加数据域：存放顶点入度
ArcNode *firstarc; //指向第一个邻接点
}VNode; //头结点类型
void TopSort(AdjGraph * G) //拓扑排序算法
{
int i,j;
int St[MAXV],top=-1; //栈St的指针为top
ArcNode * p;
for(i=0;i<G->n;i++) //入度置初值0
G->adjlist[i].count=0;
for(i=0;i<G->n;i++) //求所有顶点的入度
{
p=G->adjlist[i].firstarc;
while(p!=NULL)
{
G->adjlist[p->adjvex].count++;
p=p->nextarc;
}
}
for(i=0;i<G->n;i++) //将入度为0的顶点进栈
if(G->adjlist[i].count==0)
{
top++;
St[top]=i;
}
while(top>-1) //栈不空循环
{
i=St[top]; //出栈的一个顶点i
top--;
printf("%d",i); //输出该顶点
p=G->adjlist[i].firstarc; //找到第一个邻接点
while(p!=NULL) //将顶点i的出边邻接点的入度减1
{
j=p->adjvex;
G->adjlist[j].count--;
if(G->adjlist[j].count==0) //将入度为0的邻接点进栈
{
top++;
St[top]=j;
}
p=p->nextarc; //找下一个邻接点
}
}
}
参考伪代码：
TOPOLOGICAL-SORTING-GREEDY(g)
let inDegree be every verties inDegree Array
let stack be new Stack
let result be new Array
for v equal to every vertex in g
if inDegree[v] == 0
stack.push(v)
end
while stack.empty() == false
vertex v = stack.top()
stack.pop()
result.append(v)
for i equal to every vertex adjacent to v
inDegree[i] = inDegree[i] - 1
if inDegree[i] == 0
stack.push(i)
end
end
return result.reverse()
1.6 关键路径
AOE-网是用边去表示活动的网，它是一种带权的有向无环图，其中，顶点表示事件，弧表示活动，权表示活动持续的时间。
在AOE网中，从源点到汇点的所有路径中具有最大路径长度的路径称为关键路径。
完成整个工程的最短时间就是AOE网中关键路径的长度，或者说是AOE网中一条关键路径上各活动持续时间的总和，把关键路径上的活动称为关键活动。
2.PTA实验作业（4分）
2.1 六度空间（2分）
2.1.1 伪代码（贴代码，本题0分）
void BFS(MGraph& g,int u){
将u顶点标记
初始化dist[u]=0记录距离
将u进队列
cnt++;//用来表示几个人
while q
取出队头，判断距离dist是否大于6
循环矩阵，只要没有被标记并且有边
进队列,距离+1；标记已访问，cnt++
}
2.1.2 提交列表
2.1.3 本题知识点
-
- new申请空间：new int* [MAXV + 1]
-
- dis[]进行距离计算，visited[]进行标记
-
- 每次每个人都要将数组初始化
2.2 村村通或通信网络设计或旅游规划（2分）
2.2.1 伪代码（贴代码，本题0分）
void Dijkstra(MGraph g, int v)
{
初始化dist数组、s数组、pay数组,dist数组
遍历图中所有节点
for（i = 0; i < g.n; i++）
若s[i]！ = 0，则数组找最短路径，顶点为u
s[u] = 1进s
for（i = 0; i < g.n; i++）
if（g.edges[u][j].len < INF && dist[u] + g.edges[u][j].len < dist[j]）
则修正dist[j] = dist[u] + g.edges[u][j].len;
pay[j] = pay[u] + g.edges[u][j].pay;
else if（路径一样长但是花费更少）
则修正pay[j] = pay[u] + g.edges[u][j].pay;
}
2.2.2 提交列表
2.2.3 本题知识点
-
- 邻接矩阵，无向图
-
- 最短路径Dijkstra算法
-
- 用另一个结构体，存路径长度和费用，并用dist[]与pay[]存储
