分类问题损失函数的信息论解释

分类问题的优化过程是一个损失函数最小化的过程，对应的损失函数一般称为logloss，对于一个多分类问题，其在N个样本上的logloss损失函数具有以下形式：

其中，yi(n)代表第n个样本是否属于第i个类别，取值为0或1，f(x(n))i代表分类模型对于第n个样本属于第i个类别的预测概率。将上面的式子稍作简化就可以得到我们常见的二分类问题下的损失函数，在这里不做展开，我们下面的讨论也都对于更为一般的多分类问题展开，而这些讨论对于二分类问题显然也同样适用。

 

上面的损失函数，很容易从最大似然的角度来做理解，也就是说等号右边的部分，去掉负号以后，对应着模型的一个估计f在N个样本上（取了log）的似然函数，而似然函数的最大化就对应着损失函数的最小化。

 

但是这个损失函数还有另外一个名字，叫做cross-entropy loss，从名字可以看出，这是一个信息论相关的名字，我们这篇文章就从信息论的角度，来理解一下分类问题的损失函数。

 

重新认识熵（entropy）

 

说起熵，大家都能知道衡量的是“数据的混乱程度”，但是它具体是如何衡量的呢？让我们首先来重新认识一下熵。

 

现在是周五的下班高峰期，你站在北京东三环的一座天桥上面，望着一辆辆汽车穿梭而过。你现在肩负着一个任务：你需要告诉我你看到的每一辆车的品牌型号，而我们的通讯工具，是一个二进制的通信管道，里面只能传输0或者1，这个管道的收费是1￥/bit。

 

显然你需要设计一组二进制串，每个串对应一个车型，例如1001对应的是一辆大众桑塔纳。那么你要如何设计这一组二进制串呢？具体来说，你会为丰田凯美瑞和特斯拉ModelS设计同样长度的串吗？

 

即使你不精通概率论，你可能也不会这么做，因为你知道大街上跑着的凯美瑞肯定比ModelS多得多，用同样长度的bit来传输肯定是不经济的。你肯定会为凯美瑞设计一个比较短的串，而为ModelS设计一个长一些的串。你为什么会这么做？本质上来讲，你是在利用你对分布的先验知识，来减少所需的bit数量。那具体我们应该如何利用分布知识来对信息进行编码呢？

 

幸运的是，香农（Shannon）老先生证明了，如果你知道一个变量的真实分布，那么为了使得你使用的平均bit最少，那么你应该给这个变量的第i个取值分配log1/yi个bit，其中yi是变量的第i个取值的概率。如果我们按照这样的方式来分配bit，那么我们就可以得到最优的数据传输方案，在这个方案下，我们为了传输这个分布产生的数据，平均使用的bit数量为：

有没有很眼熟？没错，这就是我们天天挂在嘴边的熵（entropy）。

 

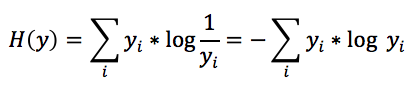
交叉熵（cross entropy）

 

在上面的例子中，我们利用我们对数据分布y的了解，来设计数据传输方案，在这个方案中，数据的真实分布y充当了一个“工具”的角色，这个工具可以让我们的平均bit长度达到最小。

 

但是在大部分真实场景中，我们往往不知道真实y的分布，但是我们可以通过一些统计的方法得到y的一个估计。如果我们用来设计传输方案，也就是说，我们给分布的第i个取值分配log1/yi个bit，结果会是怎样？

 

套用之前的式子，将log中的y替换成为y^，我们可以得到，如果使用y^作为“工具”来对数据进行编码传输，能够使用的最小平均bit数为：

 

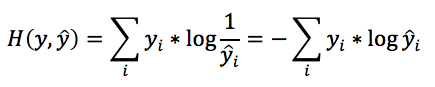
这个量，就是所谓的交叉熵（cross entropy），代表的就是使用y^来对y进行编码的话，需要使用的最短平均bit串长度。

 

交叉熵永远大于或等于熵，因为交叉熵是在用存在错误的信息来编码数据，所以一定会比使用正确的信息要使用更多的bit。只有当y^和y完全相等时，交叉熵才等于熵。

 

用交叉熵衡量分类模型质量

 

现在回到分类问题上来。假设我们通过训练得到了某模型，我们希望评估这个模型的好坏。从上面信道传输的角度来看，这个模型实际上提供了对真实分布y的一个估计y^。我们说要评估这个模型的好坏，实际是是想知道我们给出的估计y^和真实的分布y相差多大，那么我们可以使用交叉熵来度量这个差异。

 

由于交叉熵的物理意义是用y^作为工具来传输y平均需要多少个bit，那我们可以计算一下如果用y^来传输整个训练数据集需要多少个bit，首先我们看一下传输第n个样本需要多少个bit。由于估计出来的模型对于第n个样本属于第i个类的预测概率是y^i(n)，而第n个样本的真实概率分布是yi(n)，所以这一个样本也可以看做是一个概率分布，那么根据交叉熵的定义：

 那么传输整个数据集需要的bit就是：

 进一步变换可得：

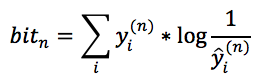
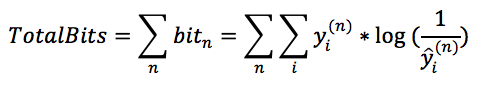
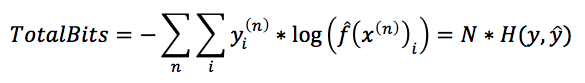
 其中。对比文章最开始的logloss损失函数可知：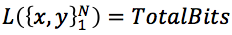

 

也就是说，分类问题的损失函数，从信息论的角度来看，等价于训练出来的模型（分布）与真实模型（分布）之间的交叉熵（两者相差一个只和样本数据量有关的倍数N），而这个交叉熵的大小，衡量了训练模型与真实模型之间的差距，交叉熵越小，两者越接近，从而说明模型越准确。

 

总结

 

通过上面的讲解，我们从信息论的角度重新认识了分类问题的损失函数。信息论和机器学习是紧密相关的两个学科，从信息论的角度来说，模型优化的本质就是在减少数据中的信息，也就是不确定性。希望这个理解角度，能够让大家对分类问题有一个更全面的认识。希望对熵有进一步了解的同学，可以读一下香农老先生的著名文章《AMathematical Theory of Communication》，有时间的同学更可以研读一下《Elements ofInformation Theory》这本巨著，一定会让你的ML内功发生质的提升。

 

本文的灵感和部分内容来自这篇文章：http://rdipietro.github.io/friendly-intro-to-cross-entropy-loss/。

来源： http://www.cnblogs.com/yymn/p/5634166.html

来自为知笔记(Wiz)