各种优化方法总结比较（sgd/momentum/Nesterov/adagrad/adadelta）

前言

这里讨论的优化问题指的是，给定目标函数f(x)，我们需要找到一组参数x，使得f(x)的值最小。

本文以下内容假设读者已经了解机器学习基本知识，和梯度下降的原理。

SGD

SGD指stochastic gradient descent，即随机梯度下降。是梯度下降的batch版本。

对于训练数据集，我们首先将其分成n个batch，每个batch包含m个样本。我们每次更新都利用一个batch的数据，而非整个训练集。即： 

xt+1=xt+Δxt

Δxt=−ηgt

其中，η为学习率，gt为x在t时刻的梯度。

这么做的好处在于：

• 当训练数据太多时，利用整个数据集更新往往时间上不显示。batch的方法可以减少机器的压力，并且可以更快地收敛。
• 当训练集有很多冗余时（类似的样本出现多次），batch方法收敛更快。以一个极端情况为例，若训练集前一半和后一半梯度相同。那么如果前一半作为一个batch，后一半作为另一个batch，那么在一次遍历训练集时，batch的方法向最优解前进两个step，而整体的方法只前进一个step。

Momentum

SGD方法的一个缺点是，其更新方向完全依赖于当前的batch，因而其更新十分不稳定。解决这一问题的一个简单的做法便是引入momentum。

momentum即动量，它模拟的是物体运动时的惯性，即更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向。这样一来，可以在一定程度上增加稳定性，从而学习地更快，并且还有一定摆脱局部最优的能力： 

Δxt=ρxt−1−ηgt

其中，ρ 即momentum，表示要在多大程度上保留原来的更新方向，这个值在0-1之间，在训练开始时，由于梯度可能会很大，所以初始值一般选为0.5；当梯度不那么大时，改为0.9。η 是学习率，即当前batch的梯度多大程度上影响最终更新方向，跟普通的SGD含义相同。ρ 与 η 之和不一定为1。

Nesterov Momentum

这是对传统momentum方法的一项改进，由Ilya Sutskever(2012 unpublished)在Nesterov工作的启发下提出的。

其基本思路如下图（转自Hinton的coursera公开课lecture 6a）：

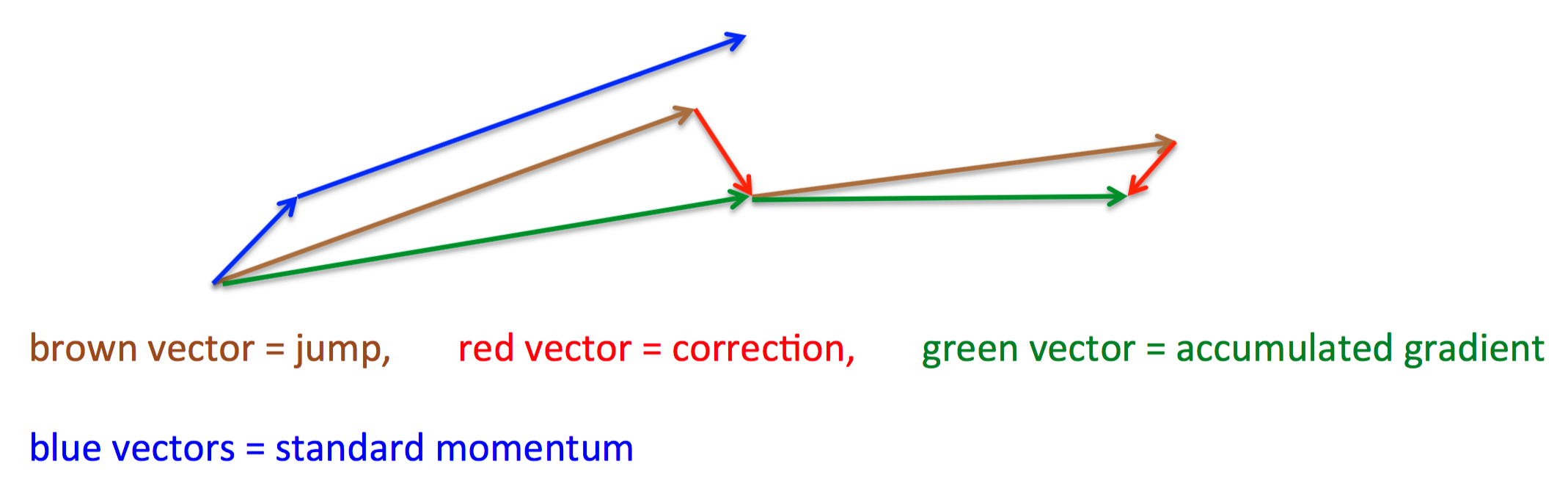
首先，按照原来的更新方向更新一步（棕色线），然后在该位置计算梯度值（红色线），然后用这个梯度值修正最终的更新方向（绿色线）。上图中描述了两步的更新示意图，其中蓝色线是标准momentum更新路径。

公式描述为： 

Δxt=ρxt−1−ηΔf(xt−1+ρxt−1)

Adagrad

上面提到的方法对于所有参数都使用了同一个更新速率。但是同一个更新速率不一定适合所有参数。比如有的参数可能已经到了仅需要微调的阶段，但又有些参数由于对应样本少等原因，还需要较大幅度的调动。

Adagrad就是针对这一问题提出的，自适应地为各个参数分配不同学习率的算法。其公式如下： 

Δxt=−η∑tτ=1gτ+ϵ−−−−−−−−−−√gt

其中gt 同样是当前的梯度，连加和开根号都是元素级别的运算。eta 是初始学习率，由于之后会自动调整学习率，所以初始值就不像之前的算法那样重要了。而ϵ是一个比较小的数，用来保证分母非0。

其含义是，对于每个参数，随着其更新的总距离增多，其学习速率也随之变慢。

Adadelta

Adagrad算法存在三个问题

• 其学习率是单调递减的，训练后期学习率非常小
• 其需要手工设置一个全局的初始学习率
• 更新xt时，左右两边的单位不同一

Adadelta针对上述三个问题提出了比较漂亮的解决方案。

首先，针对第一个问题，我们可以只使用adagrad的分母中的累计项离当前时间点比较近的项，如下式： 

E[g2]t=ρE[g2]t−1+(1−ρ)g2t

Δxt=−ηE[g2]t+ϵ−−−−−−−−√gt

这里ρ是衰减系数，通过这个衰减系数，我们令每一个时刻的gt随之时间按照ρ指数衰减，这样就相当于我们仅使用离当前时刻比较近的gt信息，从而使得还很长时间之后，参数仍然可以得到更新。

针对第三个问题，其实sgd跟momentum系列的方法也有单位不统一的问题。sgd、momentum系列方法中： 

Δx的单位∝g的单位∝∂f∂x∝1x的单位

类似的，adagrad中，用于更新Δx的单位也不是x的单位，二是1。

而对于牛顿迭代法： 

Δx=H−1tgt

其中H为Hessian矩阵，由于其计算量巨大，因而实际中不常使用。其单位为： 

Δx∝H−1g∝∂f∂x∂2f∂2x∝x的单位

注意，这里f无单位。因而，牛顿迭代法的单位是正确的。

所以，我们可以模拟牛顿迭代法来得到正确的单位。注意到： 

Δx=∂f∂x∂2f∂2x⇒1∂2f∂2x=Δx∂f∂x

这里，在解决学习率单调递减的问题的方案中，分母已经是∂f∂x的一个近似了。这里我们可以构造Δx的近似，来模拟得到H−1的近似，从而得到近似的牛顿迭代法。具体做法如下： 

Δxt=−∑t−1τ=1Δxτ−−−−−−−−√E[g2]t+ϵ−−−−−−−−√

可以看到，如此一来adagrad中分子部分需要人工设置的初始学习率也消失了，从而顺带解决了上述的第二个问题。

各个方法的比较

Karpathy做了一个这几个方法在MNIST上性能的比较，其结论是： 
adagrad相比于sgd和momentum更加稳定，即不需要怎么调参。而精调的sgd和momentum系列方法无论是收敛速度还是precision都比adagrad要好一些。在精调参数下，一般Nesterov优于momentum优于sgd。而adagrad一方面不用怎么调参，另一方面其性能稳定优于其他方法。

实验结果图如下：

Loss vs. Number of examples seen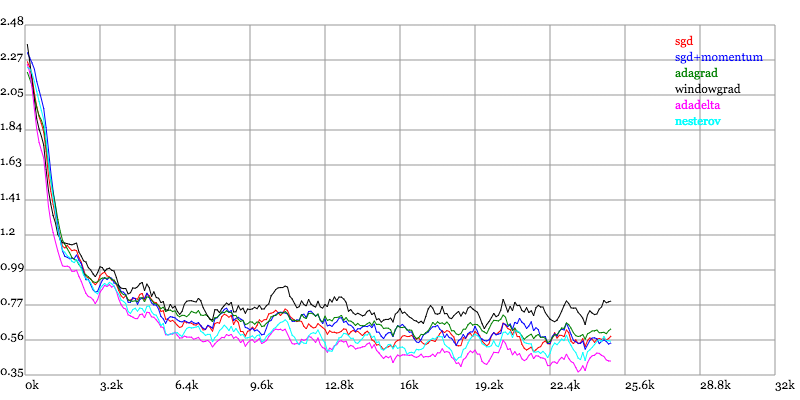 

Testing Accuracy vs. Number of examples seen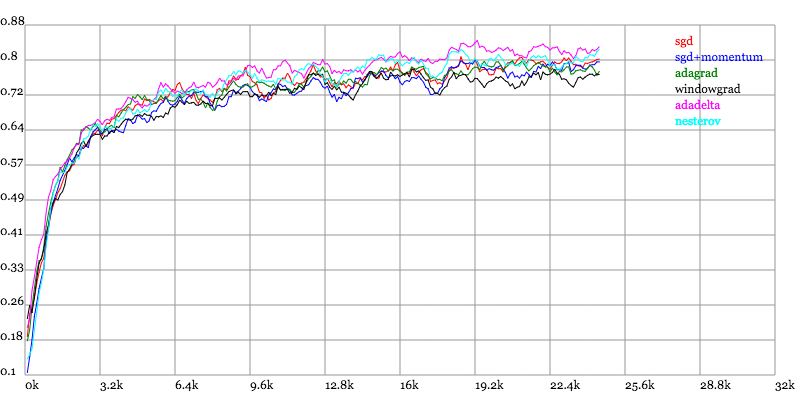 

Training Accuracy vs. Number of examples seen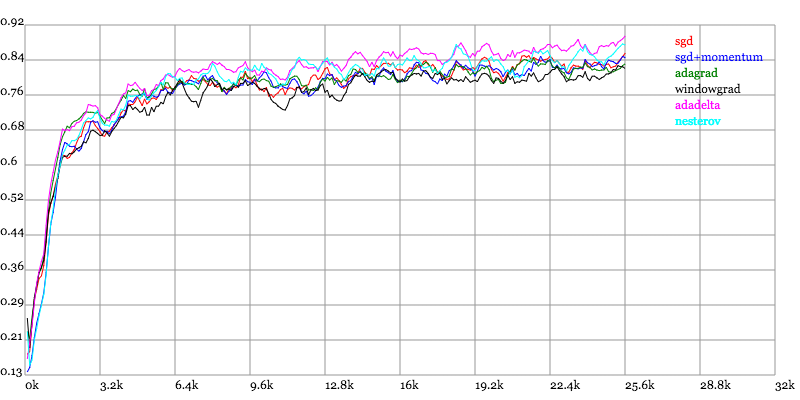

其他总结文章

最近看到了一个很棒的总结文章，除了本文的几个算法，还总结了RMSProp跟ADAM（其中ADAM是目前最好的优化算法，不知道用什么的话用它就对了）

来源： http://blog.csdn.net/luo123n/article/details/48239963

 

随机梯度下降（Stochastic gradient descent）和 批量梯度下降（Batch gradient descent ）的公式对比、实现对比

梯度下降（GD）是最小化风险函数、损失函数的一种常用方法，随机梯度下降和批量梯度下降是两种迭代求解思路，下面从公式和实现的角度对两者进行分析，如有哪个方面写的不对，希望网友纠正。

下面的h(x)是要拟合的函数，J(theta)损失函数，theta是参数，要迭代求解的值，theta求解出来了那最终要拟合的函数h(theta)就出来了。其中m是训练集的记录条数，j是参数的个数。

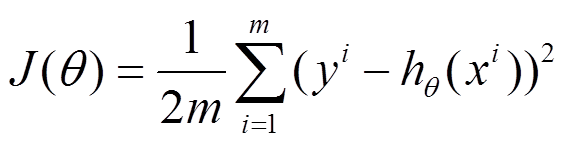
1、批量梯度下降的求解思路如下：

（1）将J(theta)对theta求偏导，得到每个theta对应的的梯度

   

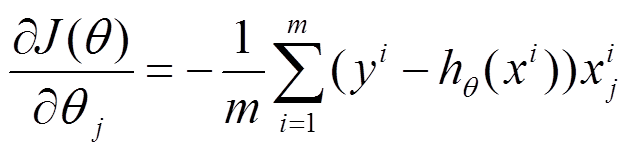
（2）由于是要最小化风险函数，所以按每个参数theta的梯度负方向，来更新每个theta

（3）从上面公式可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集所有的数据，如果m很大，那么可想而知这种方法的迭代速度！！所以，这就引入了另外一种方法，随机梯度下降。

2、随机梯度下降的求解思路如下：

（1）上面的风险函数可以写成如下这种形式，损失函数对应的是训练集中每个样本的粒度，而上面批量梯度下降对应的是所有的训练样本：

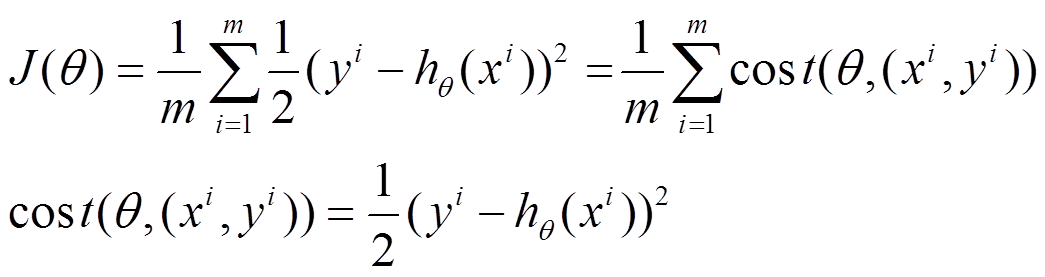
（2）每个样本的损失函数，对theta求偏导得到对应梯度，来更新theta

（3）随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

3、对于上面的linear regression问题，与批量梯度下降对比，随机梯度下降求解的会是最优解吗？

（1）批量梯度下降---最小化所有训练样本的损失函数，使得最终求解的是全局的最优解，即求解的参数是使得风险函数最小。

（2）随机梯度下降---最小化每条样本的损失函数，虽然不是每次迭代得到的损失函数都向着全局最优方向， 但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。

4、梯度下降用来求最优解，哪些问题可以求得全局最优？哪些问题可能局部最优解？

对于上面的linear regression问题，最优化问题对theta的分布是unimodal，即从图形上面看只有一个peak，所以梯度下降最终求得的是全局最优解。然而对于multimodal的问题，因为存在多个peak值，很有可能梯度下降的最终结果是局部最优。

5、随机梯度和批量梯度的实现差别

以前一篇博文中NMF实现为例，列出两者的实现差别（注：其实对应Python的代码要直观的多，以后要练习多写python！）

// 随机梯度下降，更新参数
public void updatePQ_stochastic(double alpha, double beta) {
    for (int i = 0; i < M; i++) {
        ArrayList<Feature> Ri = this.dataset.getDataAt(i).getAllFeature();
        for (Feature Rij : Ri) {
            // eij=Rij.weight-PQ for updating P and Q
            double PQ = 0;
            for (int k = 0; k < K; k++) {
                PQ += P[i][k] * Q[k][Rij.dim];
            }
            double eij = Rij.weight - PQ;

            // update Pik and Qkj
            for (int k = 0; k < K; k++) {
                double oldPik = P[i][k];
                P[i][k] += alpha
                        * (2 * eij * Q[k][Rij.dim] - beta * P[i][k]);
                Q[k][Rij.dim] += alpha
                        * (2 * eij * oldPik - beta * Q[k][Rij.dim]);
            }
        }
    }
}

// 批量梯度下降，更新参数
public void updatePQ_batch(double alpha, double beta) {

    for (int i = 0; i < M; i++) {
        ArrayList<Feature> Ri = this.dataset.getDataAt(i).getAllFeature();

        for (Feature Rij : Ri) {
            // Rij.error=Rij.weight-PQ for updating P and Q
            double PQ = 0;
            for (int k = 0; k < K; k++) {
                PQ += P[i][k] * Q[k][Rij.dim];
            }
            Rij.error = Rij.weight - PQ;
        }
    }

    for (int i = 0; i < M; i++) {
        ArrayList<Feature> Ri = this.dataset.getDataAt(i).getAllFeature();
        for (Feature Rij : Ri) {
            for (int k = 0; k < K; k++) {
                // 对参数更新的累积项
                double eq_sum = 0;
                double ep_sum = 0;

                for (int ki = 0; ki < M; ki++) {// 固定k和j之后,对所有i项加和
                    ArrayList<Feature> tmp = this.dataset.getDataAt(i).getAllFeature();
                    for (Feature Rj : tmp) {
                        if (Rj.dim == Rij.dim)
                            ep_sum += P[ki][k] * Rj.error;
                    }
                }
                for (Feature Rj : Ri) {// 固定k和i之后,对多有j项加和
                    eq_sum += Rj.error * Q[k][Rj.dim];
                }

                // 对参数更新
                P[i][k] += alpha * (2 * eq_sum - beta * P[i][k]);
                Q[k][Rij.dim] += alpha * (2 * ep_sum - beta * Q[k][Rij.dim]);
            }
        }
    }
}

来源： http://blog.csdn.net/lilyth_lilyth/article/details/8973972

梯度下降法的缺点是：

• 靠近极小值时速度减慢。
• 直线搜索可能会产生一些问题。
• 可能会'之字型'地下降。

 

三、随机梯度下降法stochastic gradient descent，也叫增量梯度下降

由于梯度下降法收敛速度慢，而随机梯度下降法会快很多

–根据某个单独样例的误差增量计算权值更新，得到近似的梯度下降搜索（随机取一个样例）

–可以看作为每个单独的训练样例定义不同的误差函数

–在迭代所有训练样例时，这些权值更新的序列给出了对于原来误差函数的梯度下降的一个合理近似

–通过使下降速率的值足够小，可以使随机梯度下降以任意程度接近于真实梯度下降

•标准梯度下降和随机梯度下降之间的关键区别

–标准梯度下降是在权值更新前对所有样例汇总误差，而随机梯度下降的权值是通过考查某个训练样例来更新的

–在标准梯度下降中，权值更新的每一步对多个样例求和，需要更多的计算

–标准梯度下降，由于使用真正的梯度，标准梯度下降对于每一次权值更新经常使用比随机梯度下降大的步长

–如果标准误差曲面有多个局部极小值，随机梯度下降有时可能避免陷入这些局部极小值中

来源： http://www.cnblogs.com/549294286/archive/2012/12/13/2817204.html

[Machine Learning] 梯度下降法的三种形式BGD、SGD以及MBGD

在应用机器学习算法时，我们通常采用梯度下降法来对采用的算法进行训练。其实，常用的梯度下降法还具体包含有三种不同的形式，它们也各自有着不同的优缺点。

下面我们以线性回归算法来对三种梯度下降法进行比较。

一般线性回归函数的假设函数为：

$h_{\theta}=\sum_{j=0}^{n}\theta_{j}x_{j}$

对应的能量函数（损失函数）形式为：

$J_{train}(\theta)=1/(2m)\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2}$

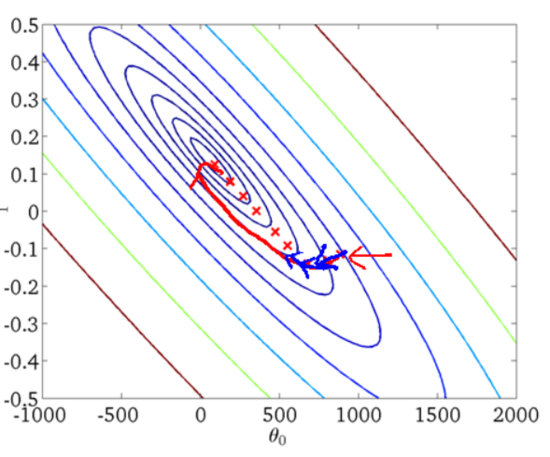
下图为一个二维参数（$\theta_{0}$和$\theta_{1}$）组对应能量函数的可视化图：

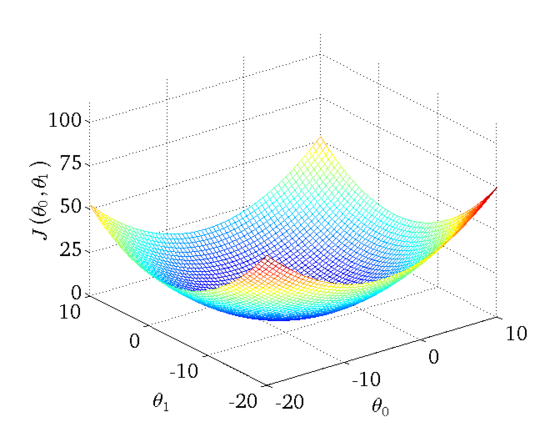
1. 批量梯度下降法BGD

批量梯度下降法（Batch Gradient Descent，简称BGD）是梯度下降法最原始的形式，它的具体思路是在更新每一参数时都使用所有的样本来进行更新，其数学形式如下：

(1) 对上述的能量函数求偏导：

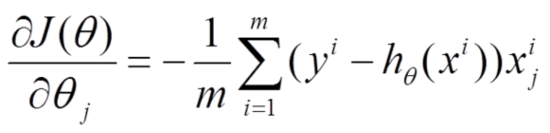
(2) 由于是最小化风险函数，所以按照每个参数$\theta$的梯度负方向来更新每个$\theta$：

具体的伪代码形式为：

repeat{

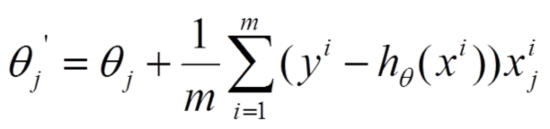
（for every j=0, ... , n）

}

从上面公式可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集所有的数据，如果样本数目$m$很大，那么可想而知这种方法的迭代速度！所以，这就引入了另外一种方法，随机梯度下降。

优点：全局最优解；

缺点：当样本数目很多时，训练过程会很慢。

从迭代的次数上来看，BGD迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下：

2. 随机梯度下降法SGD

由于批量梯度下降法在更新每一个参数时，都需要所有的训练样本，所以训练过程会随着样本数量的加大而变得异常的缓慢。随机梯度下降法（Stochastic Gradient Descent，简称SGD）正是为了解决批量梯度下降法这一弊端而提出的。

将上面的能量函数写为如下形式：

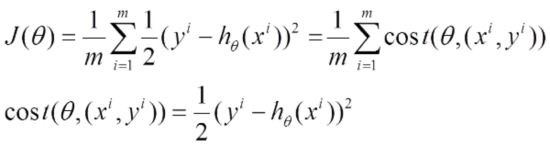
利用每个样本的损失函数对$\theta$求偏导得到对应的梯度，来更新$\theta$：

具体的伪代码形式为：

1. Randomly shuffle dataset；

2.  repeat {

for i=1, ... , $m${

(for j=0, ... , $n$)

}

}

随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

优点：训练速度快；

缺点：准确度下降，并不是全局最优。

从迭代的次数上来看，SGD迭代的次数较多，在解空间的搜索过程看起来很盲目。其迭代的收敛曲线示意图可以表示如下：

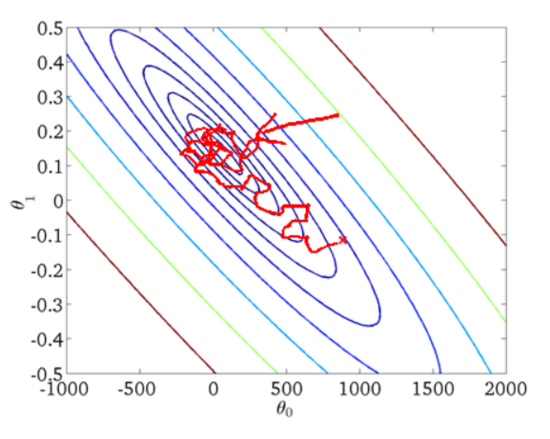
3. 小批量梯度下降法MBGD

有上述的两种梯度下降法可以看出，其各自均有优缺点，那么能不能在两种方法之间取得一个折衷呢？即，算法的训练过程比较快，而且也要保证最终参数训练的准确率，而这正是小批量梯度下降法（Mini-batch Gradient Descent，简称MBGD）的初衷。

MBGD在每次更新参数时使用b个样本（b一般为10），其具体的伪代码形式为：

Sayb=10, m=1000.

Repeat{

for i=1, 11, 21, 31, ... , 991{

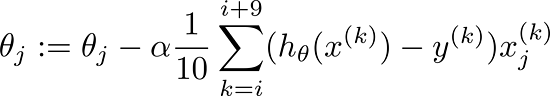
(for every j=0, ... , $n$)

}

}

4. 总结

Batch gradient descent:Use all examples in each iteration；

Stochastic gradient descent:Use 1 example in each iteration；

Mini-batch gradient descent:Use b examples in each iteration.

来源： http://www.tuicool.com/articles/qmqaIbB

来自为知笔记(Wiz)