异常检测 简介 Anomaly Detection
Anomaly Detection，也叫做 异常检测，目的在于让机器知道我所不知道的事情。
1. 什么是 Anomaly（异常）？
虽然说是 异常，但其实是以训练集为核心，判断输入数据是否与训练集中的数据 “类似”。在不同的领域可以有不同的叫法，比如：outlier Detection，novelty Detection，exceptions Detection。
至于什么才是“类似”，它的定义这取决于你所用的方法。如下图所示，如果你给的训练集只有雷丘，那么比卡丘就是“异常”；相反，如果你给的训练集是比卡丘，那雷丘就是“异常”。
1.1 问题定义 Problem Formulation
- 给定一个训练集
- 我们要找到一个函数来检测 输入 x 是不是属于训练集（是否和训练集的数据属于同一类）
1.2 为什么不能用二分类来解决这个问题？
如上面所说的，所谓“异常”，其实就是看是否和训练集“相似”，虽然我们很容易获得正训练集（如上面的雷丘），但是负训练集我们无法来决定，如果我们用 宝可梦 来作为负训练集来训练二分类，那下次输入一个 亚古兽 呢？这时候二分类模型就无法识别这个没见过的 负样本，而这样的负样本实在是太多了，我们没法穷举。如下图所示。
更坏的情况就是，很多情景下，我们没法收集到负样本。比如说刷卡行为，大多数情况都只是正常的交易行为，而盗刷这一类情况就少之又少，甚至（目前）没有。
所以异常检测无法简化成二分类来实现，这是一个独立的研究主题。
1.3 异常检测模型 分类
根据给出的训练集，我们可以大致将其分成两大类三小类：
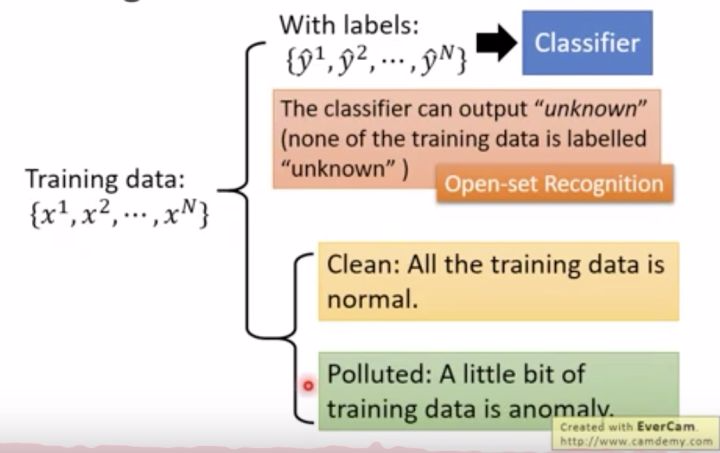
- (labeled)训练集中每个样本都有标签，用这些样本来训练一个分类器，这个分类器除了能够识别训练集中已有样本标签外，还能输出 “unknown” 标签，用来表示该输入是“没见过的”、不在训练集中的。我们把它叫做 “open-set recognition（开放式识别）”
- (unlabeled)另一种情况是，我的训练集是没有标签的
- （clean）但这个训练集是“干净”的，我们可以将这个训练集里所有的样本都视为“正样本“;
- （polluted）然而干净的数据集在现实应用中很少，大多数都是或多或少参杂着”异常样本“，而且你无法知道，比如说银行给你大量刷卡数据进行训练，而这些数据里有可能有盗刷的数据且没有标注出来。
2. Labeled（带标签）
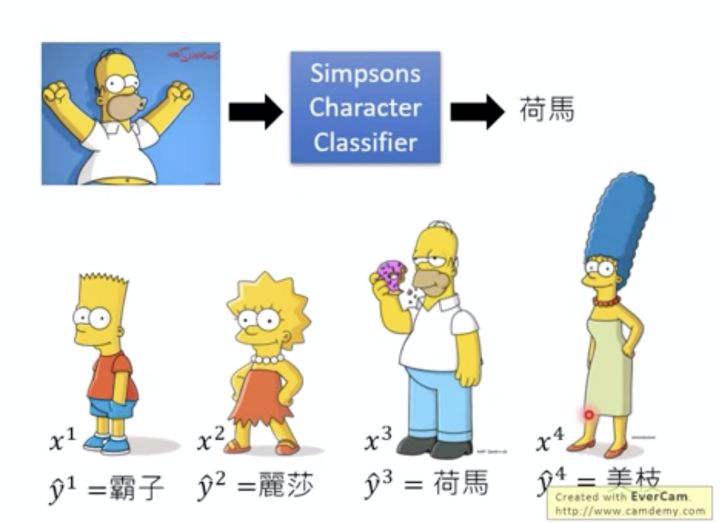
在这里就用 辛普森家族 来举例子。这里有一堆辛普森家族的人物形象及其对应的人物名称（视为标签），这样我们就能训练一个“辛普森角色分类器”，输入一个人物的形象，输出该人物的名称（标签）。
那我们训练好“辛普森角色分类器”后，这个分类器会输出两类数据：类别（预测的名字）、信心值；然后给定一个阈值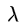 
，当信心度大于这个阈值，就视为“正常值（属于辛普森家族）”，低于则视为“异常值（不属于辛普森家族）”
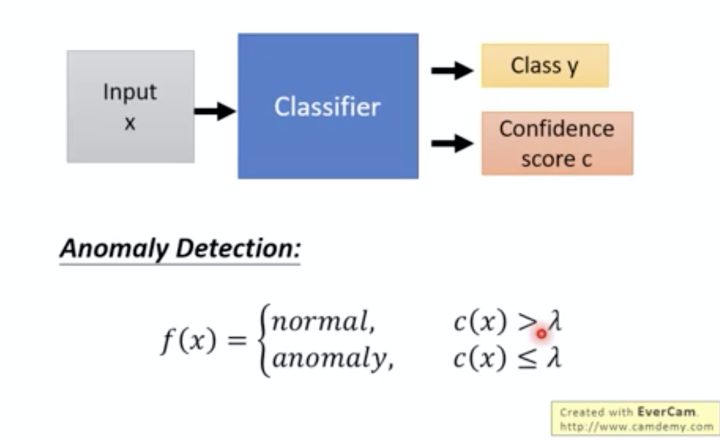
分类器的输出其实是一个概率分布(distribution)，输出前经过一个 softmax，使得这个分布中的值之和为1，其输出每一项 表示 每一个类别及其对应的信心值；我们将其中的最大值，视为分类器对该输入的信心值.
除了最高值，我们还可以用 熵（entropy）来决定分类器最后的信心值。
如下图所示，第一个分类器中，霸子的信心值很高（总体熵低），且其他很低，就说明分类器能够很好地把这个人物形象进行分类，故认为该形象是“正常值”；
而第二个分类器中，每一类的信心值都不高且均匀（最大值不高，总体熵高），说明分类器没见过该形象，信心不够，没法很好地区分，则可以认为该形象是“异常值”。
除了用分类器与其输出的分布来 判断 该分类器的信心度，当然还有其他的方式，如下图所说的，不仅输出分布（用来分类），还教分类器直接输出其信心度（直接可以判断是否异常）。
关于上面模型训练部分，一般来说我们有个“验证集”来调节模型的超参数，在“训练集”中，所有的样本都是“正样本“且有各自的标签（如都是辛普森和他们的人物名字），而在”验证集“中就没必要每个样本都有其“人物标签”，只需要判断其“是否属于辛普森家族”就行了（两个标签：属于、不属于）。
2.1 评价标准
在上面的例子中，“辛普森家族异常检测模型“其实是一个普通分类器，那我们是否也可以用准确率（Accuracy）来评估这个模型的好坏呢？答案是：这不是一个好的选择。
正如我们前面所说的，异常检测的数据集的标签分布是不均匀的，也就是说我们很大概率能够找到“正样本”而缺少“负样本”；这种情况下，如果模型“无情地”把所有的样本都预测成正样本，那准确率也会很高，这样显然是不对的。
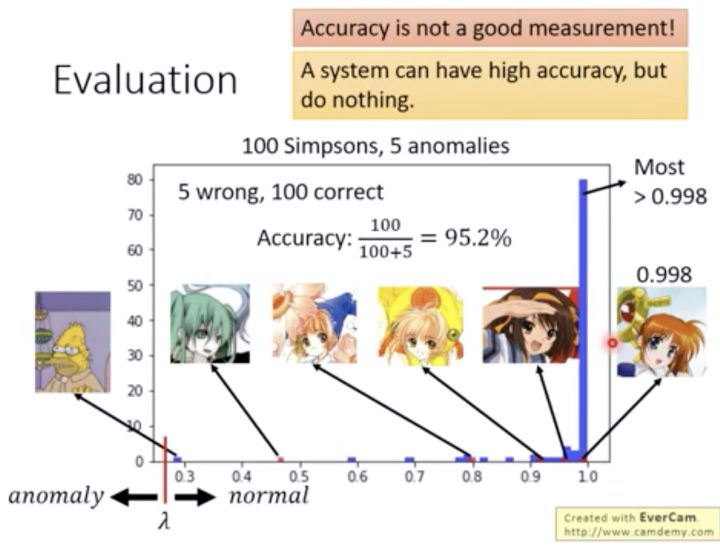
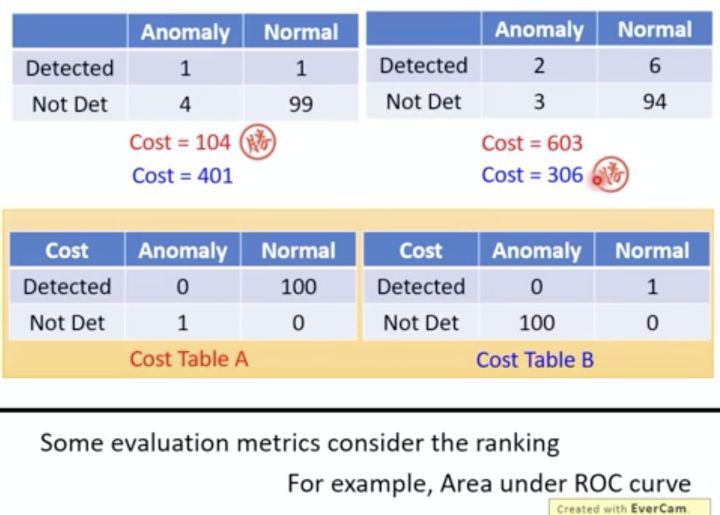
准确率对于不平衡数据没法很好地评估，其实也有很多方法来解决，比如说成本积分制： 当正常数据没有检测出，则成本为100，异常数据没有检测出，成本为1（见Cost Table A），这时候左边模型的成本则会低于右边模型的成本（红色字体），则左边的模型更优秀； 而如果正常数据没检测出的成本为1，异常数据没检测出的成本为100，这时候右边的模型就更优秀（蓝色字体）；
积分制的使用要取决于你对业务的理解：异常数据没检测出、正常数据没检测出，哪个更加重要？比如在医疗上，对于癌细胞的异常检测，宁愿检测错正常人，也不要漏过一个病人，这时候“异常数据没检测出的成本更高”。
除了积分制，还有很多方法，比如AUC、Macro-F1等等。
2.2 存在的问题
分类器也许可以能够对“一般异常”进行“识别”，比如下面猫狗的分类器，就能够把羊驼和马来貘识别为“异常”，然而有一些“异常数据”则没那么容易了，比如说老虎和狼，这就是模型泛化问题；
因为模型一般只会抽取出一类图片中的共同特征，而此时“异常数据”无意中也具备了这一共同特征，那么就会出现把狼识别成狗的情况了。
另一个例子就是上面的“辛普森家族分类器”，将人物涂黄后，模型就会进一步识别成“丽莎”，这就说明了模型识别丽莎靠的是颜色，这显然是不正确的。
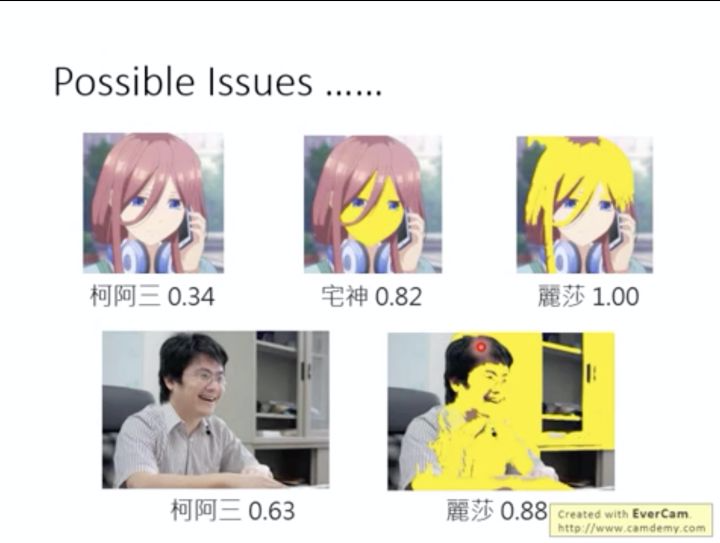
针对以上存在的问题，也有很多工作试图去解决，比如说收集一些“异常数据”，让分类器去学习给它们更低的信心值；然而我们一开始就说了，异常数据很难获取，那我们就想：能不能自动生成“异常数据”？
这时候我们就可以用GAN来尝试生成“有点像正常数据却又没那么像”的异常数据。
下面给出了相关文献，有兴趣的可以去了解一下。
3. Without Labels(不带标签的)
这一部分，就是得到了没有标签的数据。该问题的定义和带标签的分类器一样，都是根据训练集训练模型，然后帮我分析输入数据相较于训练集是否属于异常数据。与分类器给出的信心值不同，这一类的模型给出的是一个概率，如果概率大于某个阈值，才认为是正常值；
在这一部分，用一个游戏举个例子：Twitch Plays Pokemon。这个游戏是一个多人同时“玩一个角色”的在线游戏，然而和我们平时玩的网游不一样，在这个游戏中，下一步动作取决于所有在线用户的操作（如下图的右边，是每一个用户按下的指令）。
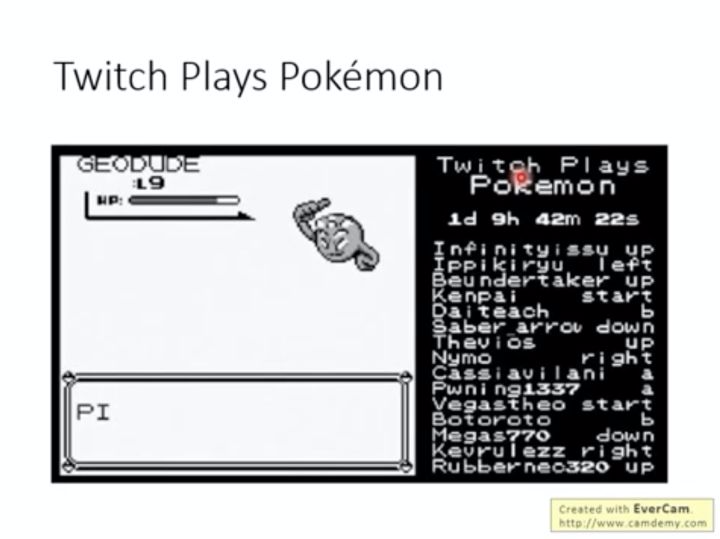
然而玩这个游戏的人非常崩溃，因为这个游戏很难进行下去（因为要所有在线玩家都给一个角色发送指令，而每个玩家的指令又不相同，而游戏只会执行其中一个指令）。所以玩家们就在想：是不是有些“恶意玩家”在乱发送指令，阻止游戏进程？也就是说是不是有人不想让这个游戏结束。
这样我们就有需求——找出“恶意用户”。在这之前，我们先有个假设：大部分玩家都希望完成这个游戏（也就是说大部分都是正常数据），而这部分数据我们会用来训练。然后我们使用异常检测，找出其中的“恶意玩家”（异常数据）。
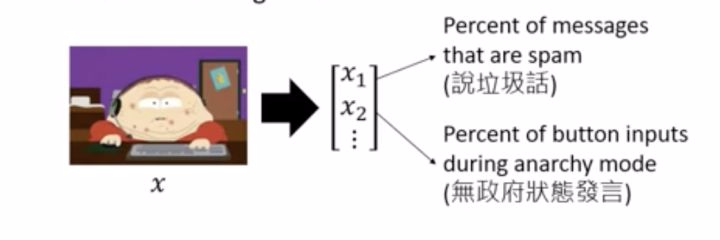
接下来，我们就要对其进行建模。在这里，我们的需求是把一堆“无标签”玩家分为正常用户和异常用户，这时我们需要把用户表示成一个向量，这样才能输入进我们的模型；而向量中的每一项可以表示这个用户的一种行为。
如下图， x1 表示这个用户过去一段时间内说垃圾话的频率（垃圾话是指游戏指令之外的话，多余的，不影响游戏进程）, x2 表示的是这个用户过去一段时间内，随机机制下的发言频率。
这个游戏有两种机制：投票机制和随机机制 投票机制：20秒内最多玩家输入的指令，则作为游戏下一步的指令； 随机机制：随机选择在线玩家输入的指令，作为游戏下一步的指令。
输入定义好了，我们就可以看看输出：模型会输出一个概率 P(x) ，和分类器不一样，无标签训练模型没有对应的Y值（标签）和信心值，只会输出一个概率 P(x) ；而和分类器相似的是，我们一样有一个
，当
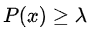时，视为正常数据；当
时，视为异常数据。如下图所示。
假设我们现在已经获取了大量用户的数据，下图是这些数据可视化展示。从可视化中可以获得一些信息：
- 在随机机制下，用户就越喜欢发指令（左上图）；
- 大部分用户都会或多或少地乱输入指令（说垃圾话，右下图）。
这时候，我们就可以很直观地看到，但用户落在左上角的位置，则很大可能这就是一个“正常玩家”，而用户落在靠右或者靠下的位置，则很大可能是“异常玩家”。
然而，我们需要一个数值化的表示方法，给每一个玩家一个分数。
假设我们之前看到的图，图上面所有的点都是由一个概率密度函数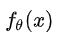
生成的（不懂也没关系，就当它是一个函数就行了），
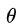是该函数的参数，决定了这个函数“长什么样”，是未知的，需要从数据中学习。
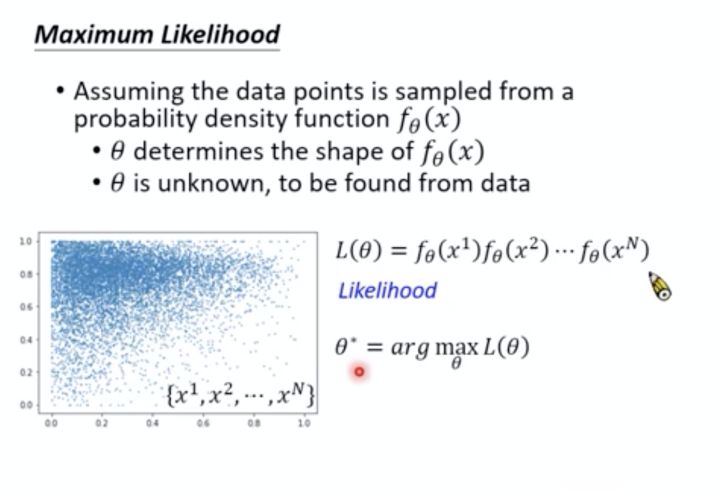
而我们的工作就变成了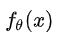： 它究竟长什么样？这时候我们就需要一个“Likelihood”的概念，意思就是说，根据我们的概率密度函数 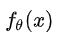，能够产生这样的已知数据的概率有多大。
如果严格来说，
而这个“Likelihood”要怎么算呢，它其实就等于每项已知数据根据 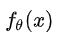这个函数所产生出来的概率的乘积；于是我们就有下面这条公式，很显然，这个公式是由 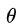来控制的，不同的 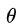，就会有不同的 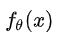，就会算出不同的“Likelihood”
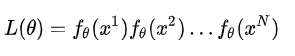
这时候，我们并不知道 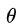是多少，但我们知道，这个 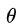，能够使我们的“Likelihood”最大化
上面是只是一个抽象的说法。在这里，我们为了让大家更好理解，我们就假设概率密度函数 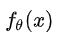为常用的高斯分布（Gaussian Distribution），这个概率密度函数并不简单，大家看不懂也没关系，就当它是一个普通函数就可以了，输入一个向量x，输出这个x被采样到的概率 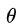；而我们前面提到需要学习的 P(x) ，在这里就等于这里需要学习的均值
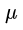和协方差矩阵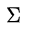 
为什么这里选择高斯分布？
其实这只是举例子，
这时候，Likelihood方程就会置换成下图的形式，用来找出能使Likelihood最大化的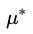 
和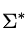 
。
左图给了一个很好的示例，告诉我们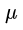， 的取值，如何影响Likelihood的取值；左上角时，数据落在这个区域的概率就很大，这时候Likelihood就很大，而右下角时，落在这个区域的概率就小，这是Likelihood就小。
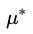和 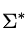其实是有公式算出来的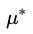， 就是所有的训练数据的向量做一个平均（输入向量是二维的，所以 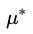也是二维的），而 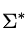就看图的右下角这个公式，这里很简单。
在这里，我们已经得到了 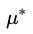和 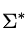，我们可以用来做异常检测，我们把测试数据代入我们的高斯分布方程，我们就能算出其概率，如果这个概率大于阈值 ，是认为是正常值，否则视为异常值。
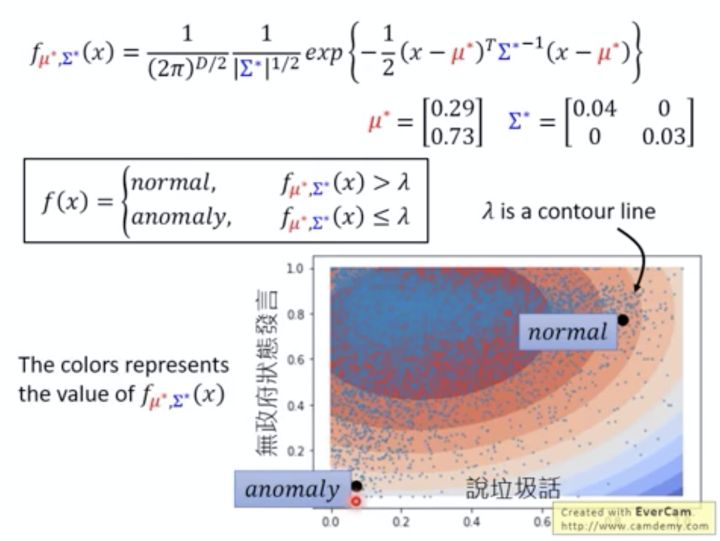
如果我们用这个训练好的方程，大概就是下图右下角的样子，颜色越深代表这个方程输出的数值就越大，就越代表“正常玩家”，而颜色越浅越蓝的，就代表“异常玩家”；而这个阈值 ，其实其中一条等高线；右下图就给出了正常点和异常点的位置示意。
以上的例子，我们只是使用了两个特征，也就是输入向量x只是二维；而机器学习的好处就是可以处理更多特征，只要你想到的，都可以加进去。下图就增加到5个特征，再训练一个Likelihood，从而获得“更准确的”异常检测效果。
3.1 更多的方法
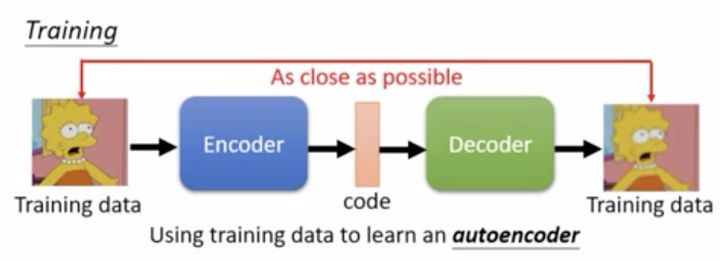
除了上面的方法，还有一种常用方法是：Auto-encoder（自动编码器），如下图所示，Encoder（编码器）先把辛普森的照片编码成一个code（隐含层），然后Decoder（解码器）把code解码回原来的的照片，训练时会同时训练编码器和解码器，尽量让解码后的照片和原照片尽可能相似（甚至相同）。这时候如果用Auto-encoder来识别一张“异常图片”，这时候的解码器是无法重构回原来的照片，通过计算重构后的照片和原照片的“距离”（或者说是相似度、还原度），就可以区分该照片是不是“异常值”。
在我看来，Auto-encoder比分类器多了一重保障（指Decoder解码器），在分类器上，找到对应的特征，就进行判断，比如颜色、轮廓等等，上面就有例子说明这样的情况并不可靠；而解码器就是一种利用特征的过程，我利用编码器提取的特征，看是否能够重构回原来照片，就能知道这是不是异常值；
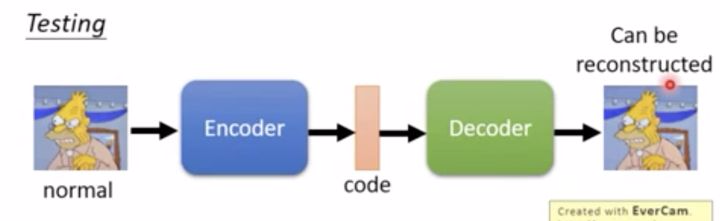
下图是正常的图片，可以看到模型很容易就重构了回来，而且和原图非常接近。因为这个模型看过辛普森，所以非常“擅长”还原辛普森。
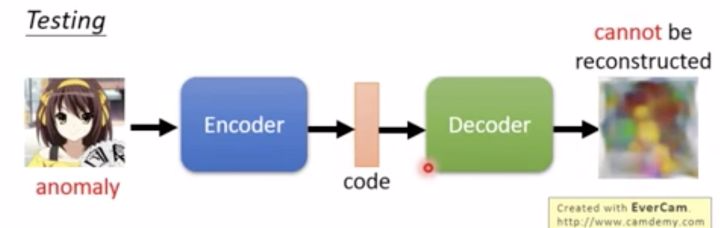
如下图的Testing阶段，对比原图和重构图，我们可以看到，编码器提取到的应该是“黄色”和“棕色”这两个特征，然而编码器用两个特征构建出来的图片，显然和原图相差甚远，这时候就可以识别为“异常值”。（从重构图可以隐约看到，这大概也是一个辛普森角色）
除了自动编码器，还有很多其他模型可以做这样的事，比如one-class SVM，Isolated Forest。有兴趣的可以自行进一步学习。
4. 应用
异常检测的应用非常广泛，下面几项是非常常见的：
- Fraud Detection（欺诈识别）
- 训练集：正常的刷卡行为；输入x：盗刷行为？
- Network Intrusion Detection（网络入侵检测）
- 训练集：正常的访问；输入x：攻击行为？
- Cancer Detection（癌症检测）
- 训练集：正常细胞；输入x：癌细胞
来源： https://zhuanlan.zhihu.com/p/116235115
欢迎转载，转载请保留页面地址。帮助到你的请点个推荐。
