神经网络前向传播和反向传播公式 详细推导
神经网络的前向传播和反向传播公式详细推导
本篇博客是对Michael Nielsen所著的《Neural Network and Deep Learning》第2章内容的解读，有兴趣的朋友可以直接阅读原文Neural Network and Deep Learning。
对神经网络有些了解的人可能都知道，神经网络其实就是一个输入XX到输出YY的映射函数：f(X)=Yf(X)=Y，函数的系数就是我们所要训练的网络参数WW，只要函数系数确定下来，对于任何输入xixi我们就能得到一个与之对应的输出yiyi，至于yiyi是否符合我们预期，这就属于如何提高模型性能方面的问题了，本文不做讨论。
那么问题来了，现在我们手中只有训练集的输入XX和输出YY，我们应该如何调整网络参数WW使网络实际的输出f(X)=Y^f(X)=Y^与训练集的YY尽可能接近？
在开始正式讲解之前，让我们先对反向传播过程有一个直观上的印象。反向传播算法的核心是代价函数CC对网络中参数（各层的权重ww和偏置bb）的偏导表达式
。这些表达式描述了代价函数值CC随权重ww或偏置bb变化而变化的程度。到这里，BP算法的思路就很容易理解了：如果当前代价函数值距离预期值较远，那么我们通过调整ww和bb的值使新的代价函数值更接近预期值（和预期值相差越大，则ww和bb调整的幅度就越大）。一直重复该过程，直到最终的代价函数值在误差范围内，则算法停止。
BP算法可以告诉我们神经网络在每次迭代中，网络的参数是如何变化的，理解这个过程对于我们分析网络性能或优化过程是非常有帮助的，所以还是尽可能搞透这个点。我也是之前大致看过，然后发现看一些进阶知识还是需要BP的推导过程作为支撑，所以才重新整理出这么一篇博客。
前向传播过程
在开始反向传播之前，先提一下前向传播过程，即网络如何根据输入XX得到输出YY的。这个很容易理解，粗略看一下即可，这里主要是为了统一后面的符号表达。
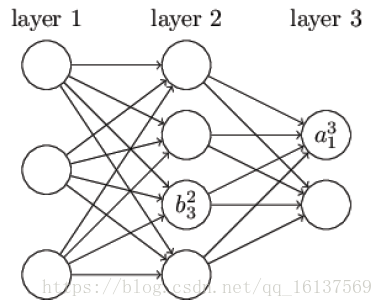
记wljkwjkl为第l−1l−1层第kk个神经元到第ll层第jj个神经元的权重，bljbjl为第ll层第jj个神经元的偏置，aljajl为第ll层第jj个神经元的激活值（激活函数的输出）。不难看出，aljajl的值取决于上一层神经元的激活：
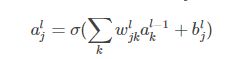
将上式重写为矩阵形式：
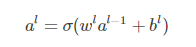
为了方便表示，记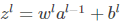
为每一层的权重输入，(2)(2)式则变为al=σ(zl)al=σ(zl)。
利用(2)(2)式一层层计算网络的激活值，最终能够根据输入XX得到相应的输出Y^Y^。
反向传播过程
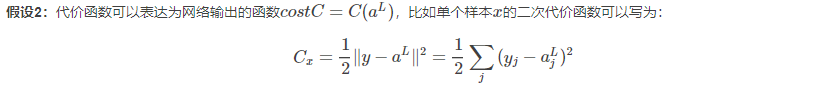
反向传播的四个基本方程
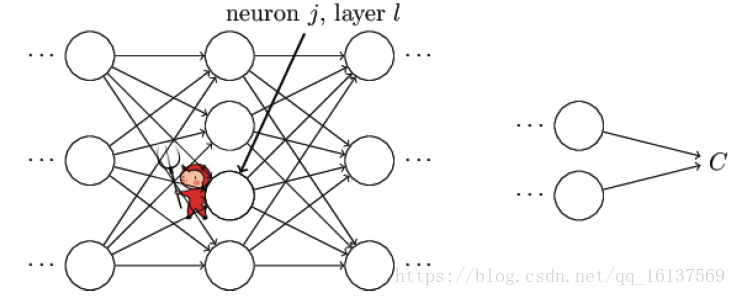
如上图所示，假设有个小恶魔在第ll层第jj个单元捣蛋，他让这个神经元的权重输出变化了ΔzljΔzjl，那么这个神经元的激活输出为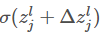
，然后这个误差向后逐层传播下去，导致最终的代价函数变化了
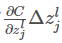。现在这个小恶魔改过自新，它想帮助我们尽可能减小代价函数的值（使网络输出更符合预期）。假设
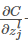一开始是个很大的正值或者负值，小恶魔通过选择一个和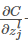方向相反的ΔzljΔzjl使代价函数更小（这就是我们熟知的梯度下降法）。随着迭代的进行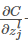，会逐渐趋向于0，那么ΔzljΔzjl对于代价函数的改进效果就微乎其微了，这时小恶魔就一脸骄傲的告诉你：“俺已经找到了最优解了（局部最优）”。这启发我们可以用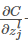来衡量神经元的误差：
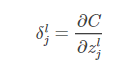
下面就来看看四个基本方程是怎么来的。
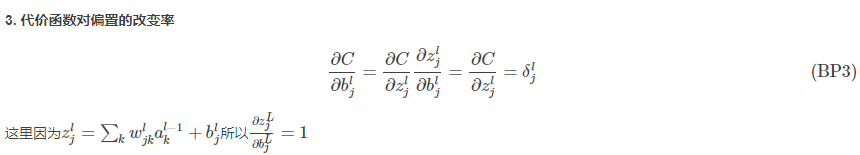
反向传播为什么快
回答这个问题前，我们先看一下普通方法怎么求梯度。以计算权重为例，我们将代价函数看成是权重的函数C=C(w)C=C(w)，假设现在网络中有100万个参数，我们可以利用微分的定义式来计算代价函数对其中某个权重wjwj的偏导：
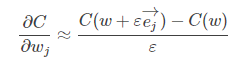
欢迎转载，转载请保留页面地址。帮助到你的请点个推荐。
