《机器学习》第二次作业——第四章学习记录和心得
目录
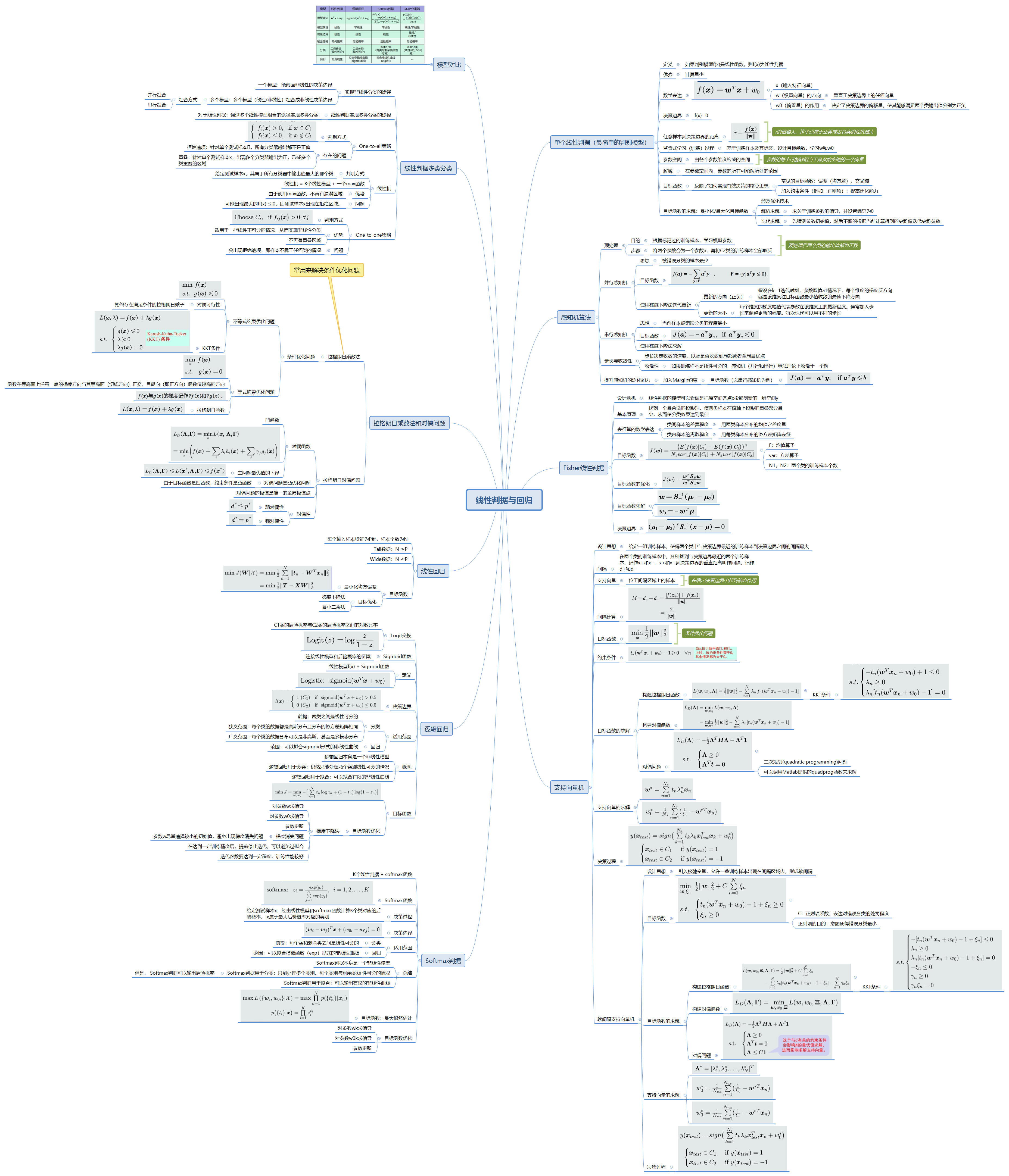
第四章 线性判据与回归
4.1、 线性判据基本概念
定义
- 如果判别模型f(x)是线性函数,则f(x)为线性判据。
- 可以用于两类分类
- 也可以用于多类分类,相邻两类之间的决策边界也是线性的。
优势
- 计算量少:在学习和分类过程中,线性判据方法都比基于学习概率分布的方法计算量少。
- 适用于训练样本较少的情况。
数学表达
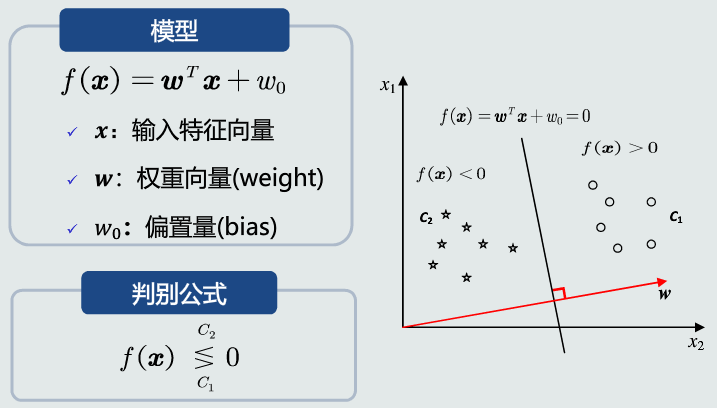
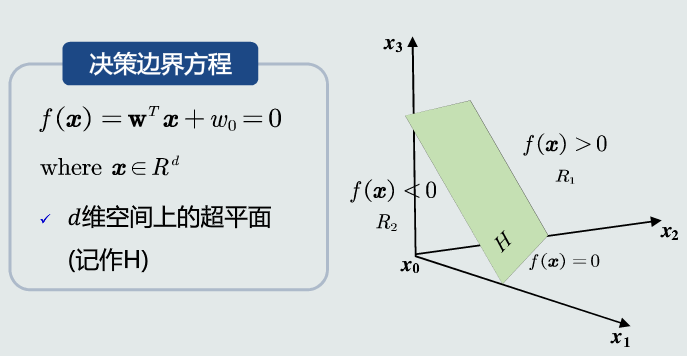
决策边界
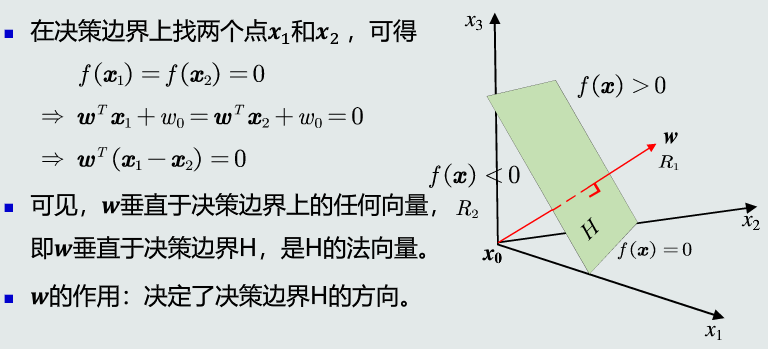
w的方向
w0的作用
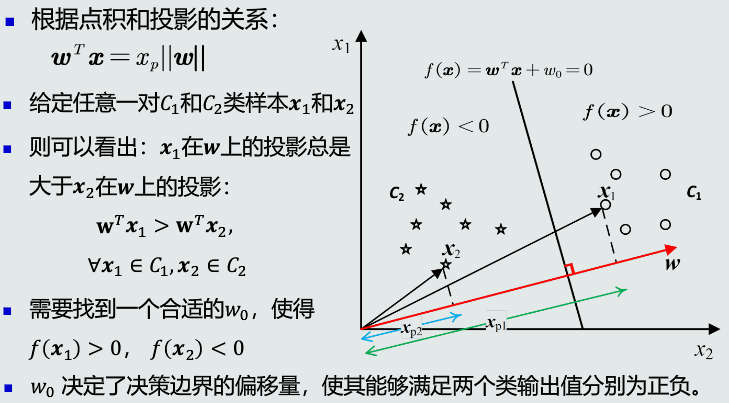
任意样本到决策边界的距离
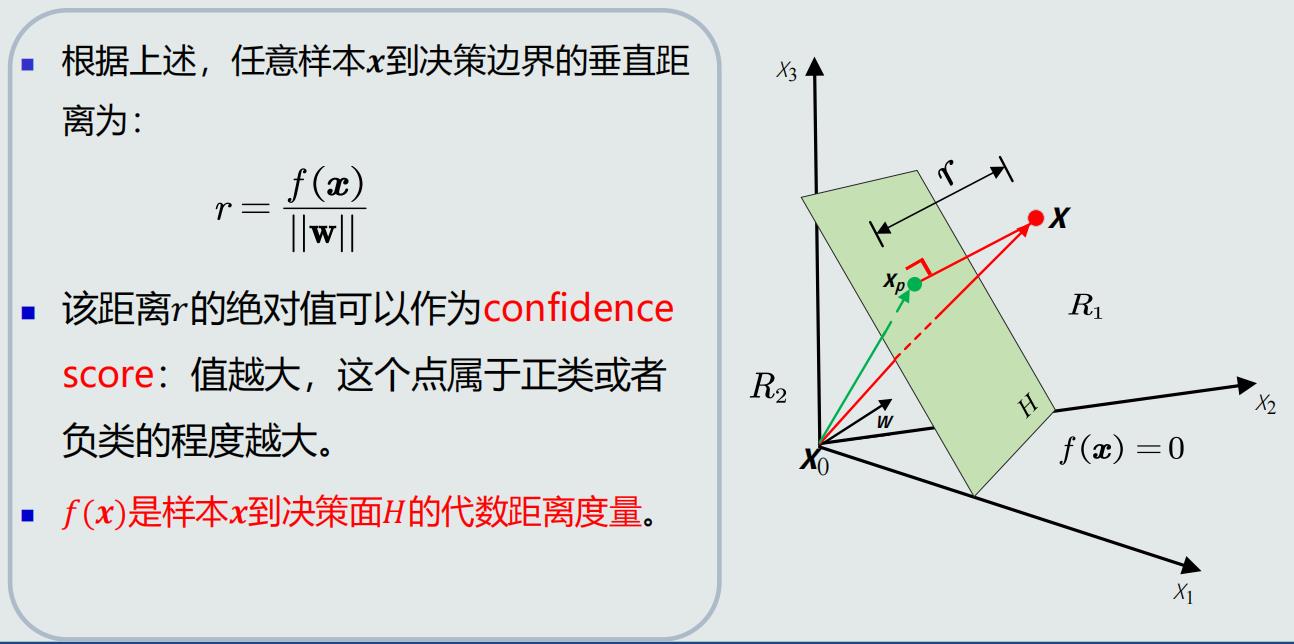
决策边界到坐标原点的距离
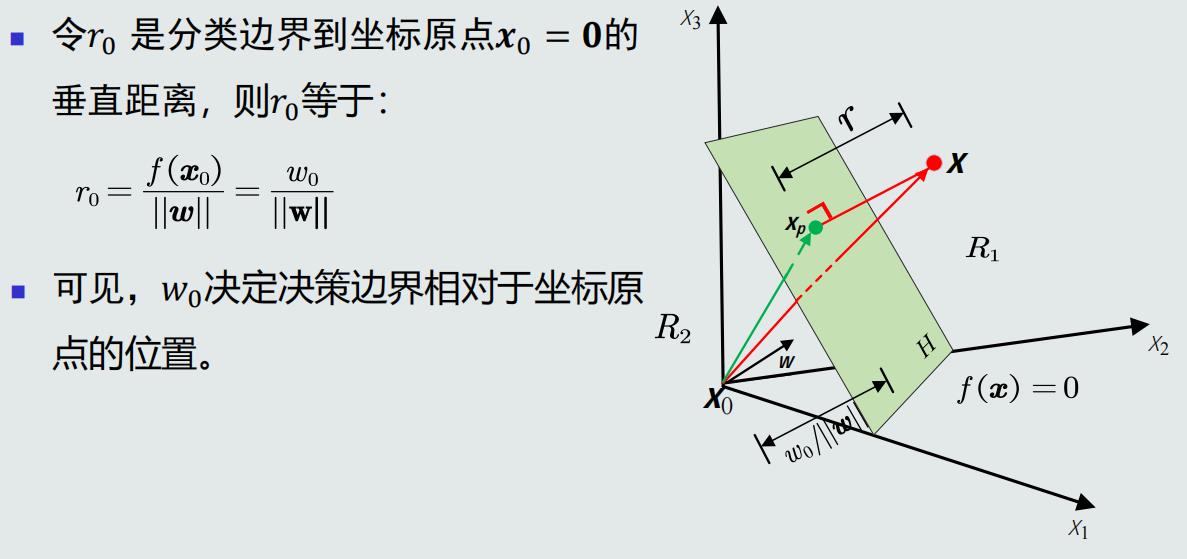
4.2、 线性判据学习概述
线性判据:学习和识别过程

参数空间&解域
- 参数空间:由各个参数维度构成的空间
- 解域:在参数空间内,参数的所有可能解所处的范围
- 参数的每个可能解相当于是参数空间的一个向量
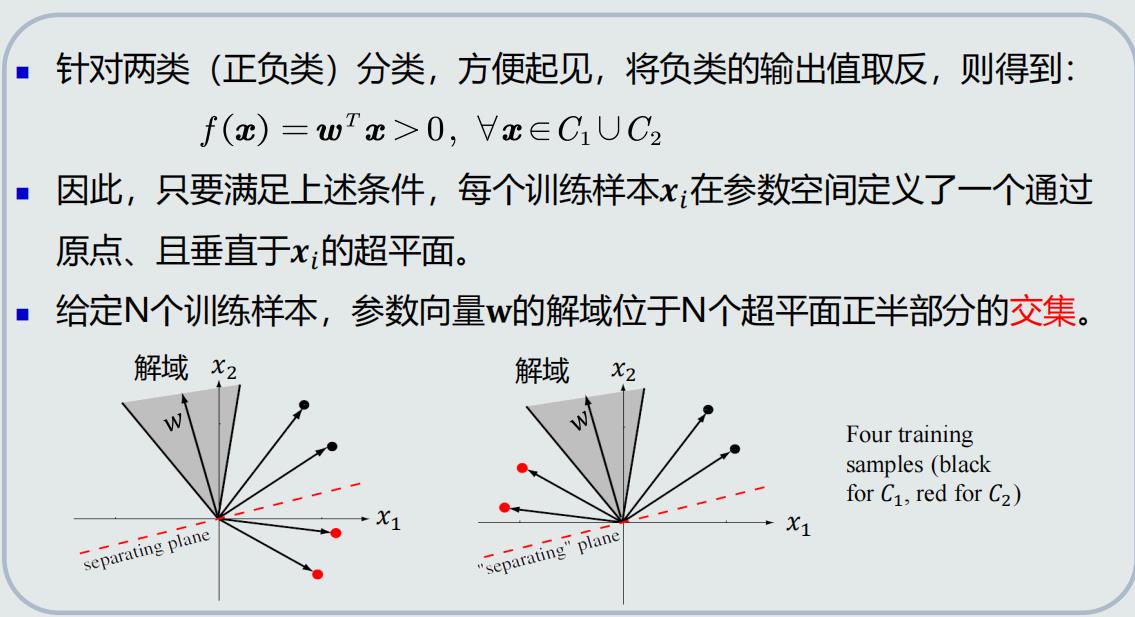
目标函数

目标函数的求解:最小化/最大化目标函数
- 涉及优化技术
- 解析求解:求关于训练参数的偏导,并设置偏导为0
- 迭代求解:先猜测参数初始值,然后不断的根据当前计算得到的更新值迭代更新参数
加入约束条件

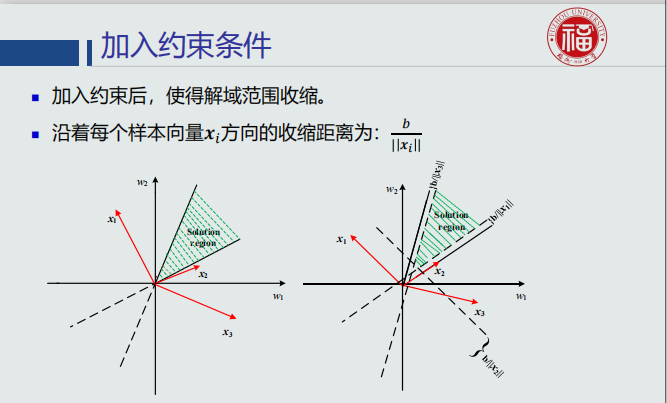
4.3、 并行感知机算法
感知机算法:预处理

几何解释
- 在几何上,通过在特征空间上增加一个维度,使得决策边界可以通过原点(𝑤0项)
- 翻转𝐶2类的样本:得到一个平面使得所有样本位于该平面同一侧
并行感知机:目标函数


梯度下降法
- 使用当前梯度值迭代更新参数。更新的方向(正负):假设在k=1迭代时刻,参数取值𝒂1情况下,每个维度的梯度反方向就是该维度往目标函数最小值收敛的最速下降方向
- 更新的大小:每个维度的梯度幅值代表参数在该维度上的更新程度。通常加入步长(𝜂𝑘)来调整更新的幅度。每次迭代可以用不同的步长
并行感知机:参数更新

并行感知机:算法流程

4.4、 串行感知机算法
串行感知机


串行感知机:算法流程

- 收敛性:如果训练样本是线性可分的,感知机(并行和串行)算法理论上收敛于一个解
- 步长决定收敛的速度、以及是否收敛到局部或者全局最优点。
- 如果目标函数J(a)满足L-Lipschitz条件(对于任意a,存在一个常数L,使得|J(a)|<L成立),则步长𝜂 = 1/ 2𝐿 可确保收敛到局部最优点。
- 如果目标函数J(a)是凸函数,局部最优点就是全局最优点。
感知机变体:加入Margin约束


4.5、 Fisher线性判据
Fisher判据设计动机&基本原理
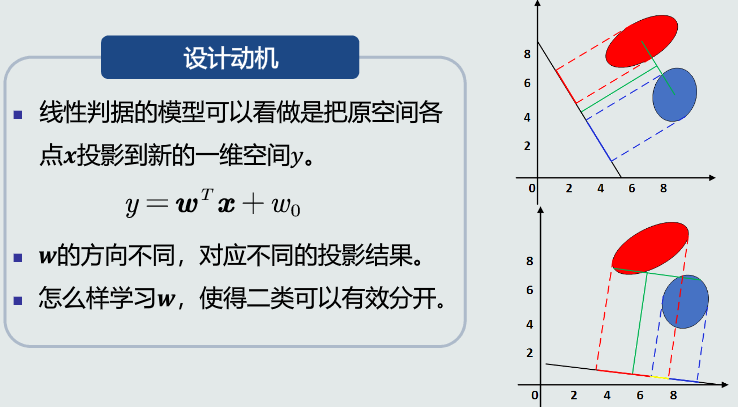

表征量的数学表达:
- 类间样本的差异程度:用两类样本分布的均值之差度量
- 类内样本的离散程度:用每类样本分布的协方差矩阵表征
Fisher线性判据:目标函数

目标函数的优化


最优参数解


Fisher线性判据:决策边界
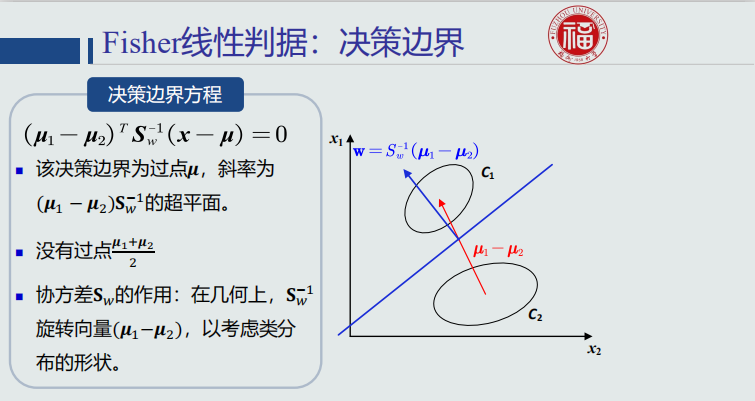
Fisher线性判据:训练算法流程

4.6、 支持向量机基本概念
支持向量机:设计动机
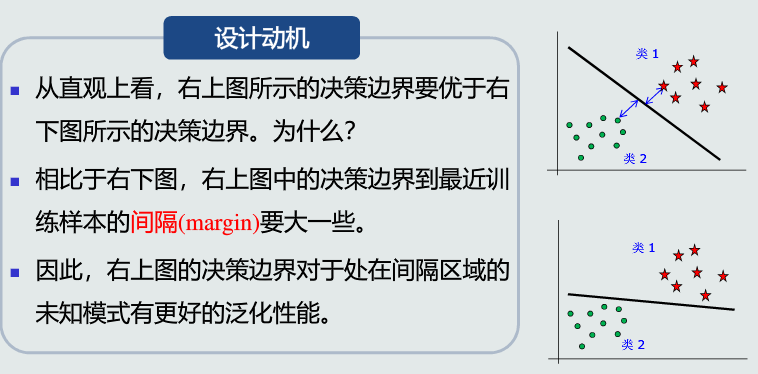
- 设计思想: 给定一组训练样本,使得两个类中与决策边界最近的训练样本到决策边界之间的间隔最大
- 间隔:在两个类的训练样本中,分别找到与决策边界最近的两个训练样本,记作𝒙+和 𝒙− 。𝒙+和𝒙−到决策边界的垂直距离叫作间隔,记作𝑑+和𝑑−
支持向量的概念
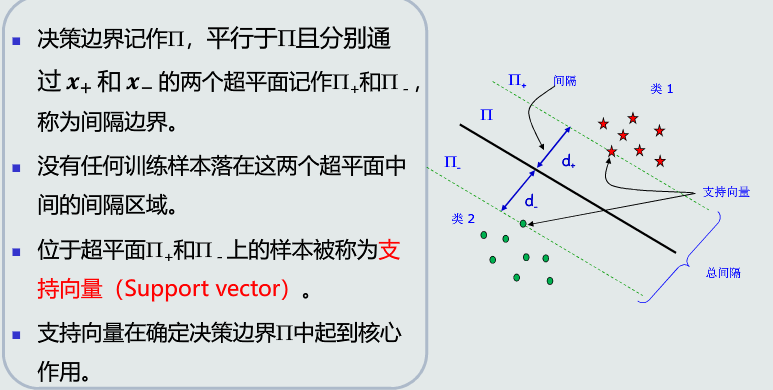
间隔计算
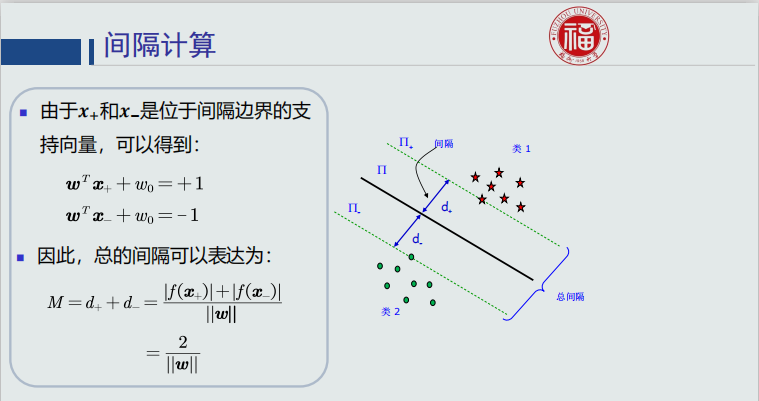
支持向量机:目标函数


4.7、 拉格朗日乘数法
- 支持向量机的目标函数是一个条件优化问题,拉格朗日乘数法是常用的解决该类问题的方法
条件优化问题

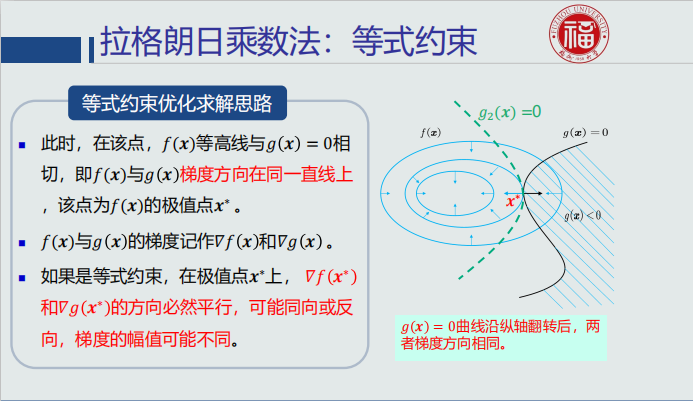
拉格朗日乘数法:等式约束
- 函数在等高面上任意一点的梯度方向与其等高面(切线方向)正交,且朝向(即正方向)函数值较高的方向
- 𝑓(𝒙)的极值点𝒙∗必须位于曲线𝑔(𝒙)=0上。沿着𝑔(𝒙)= 0的切线方向、向着𝑓(𝒙)负梯度方向移动。当出现沿着切线方向、无法再向𝑓(𝒙)负梯度方向移动时停止
- 𝑓(𝒙)负梯度方向,即梯度下降最快方向,𝑓(𝒙)取值沿着该方向不断减小

拉格朗日乘数法:不等式约束
-
情况1:极值点落在可行域内,直接通过𝛻𝑓(𝒙)= 0获得极值点
-
情况2:极值点落在可行域边界,g(x)=0,搜寻极值点𝒙∗:当出现沿着g(x)= 0切线方向、无法再向𝑓(𝒙)负梯度方向移动时停止。在该点,𝑓(𝒙)等高线与g(x)= 0相切,该点为𝑓(𝒙)的极值点𝒙∗ 。对于不等式约束,在极值点𝒙∗,𝑓(𝒙)与g(x)的负梯度方向平行且相反。梯度的幅值可能不同
-
综合两种情况:

不等式约束:KKT条件
- 在𝑔(X)≤ 0约束条件下最小化𝑓(𝒙)的问题,可以转化为如下约束条件(KKT条件)下的拉格朗日函数优化问题


4.8、 拉格朗日对偶问题
拉格朗日对偶函数

主问题最优值的下界

对偶问题

对偶函数凹凸性
- 对偶函数是以𝚲和𝚪为自变量的、与𝒙无关
- 因此,里面的拉格朗日函数𝐿看做关于对偶变量𝚲和𝚪的仿射组合
- 对偶函数𝐿𝐷则是拉格朗日函数𝐿的逐点最小值函数

- 由于目标函数是凹函数,约束条件是凸函数,所以对偶问题是凸优化问题
- 凸优化的性质:局部极值点就是全局极值点
弱对偶性
- 设对偶问题的最优值为𝑑∗、主问题的最优值为𝑝∗
- 对于所有的优化问题都存在:𝑑∗≤𝑝∗
强对偶性

4.9、 支持向量机学习算法
构建拉格朗日函数

构建对偶函数


对偶问题

对偶问题求解

求解支持向量



支持向量机:决策过程

4.10、 软间隔支持向量机
设计思想
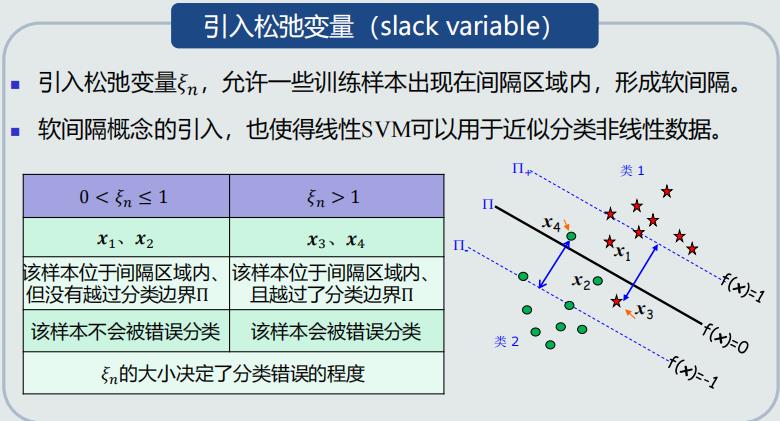

构建目标函数

构建拉格朗日函数


构建对偶函数
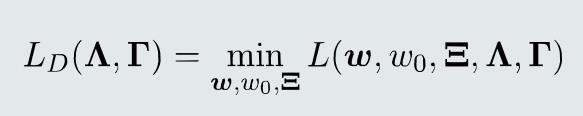


对偶问题

支持向量


参数最优解


决策过程

4.11、 线性判据多类分类
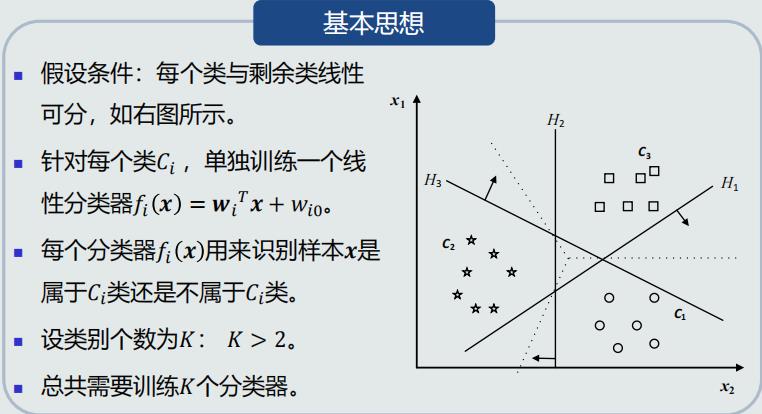
实现非线性分类的途径
- 一个模型:能刻画非线性的决策边界
- 多个模型:多个模型(线性/非线性)组合成非线性决策边界
- 组合方式:并行组合、串行组合
线性判据实现多类分类的途径
- 对于线性判据:通过多个线性模型组合的途径实现多类分类
One-to-all策略
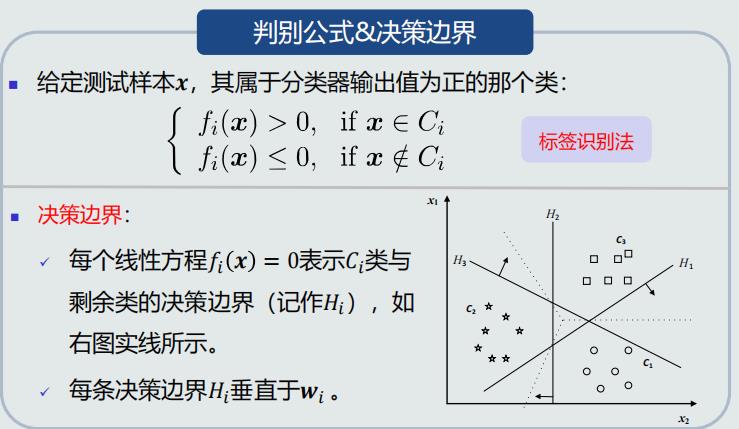
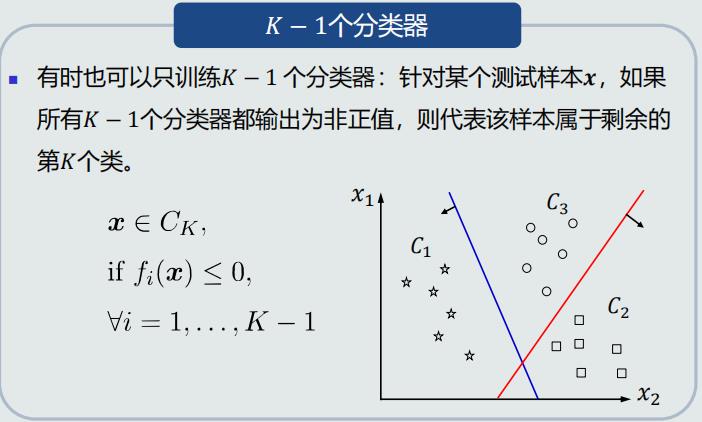
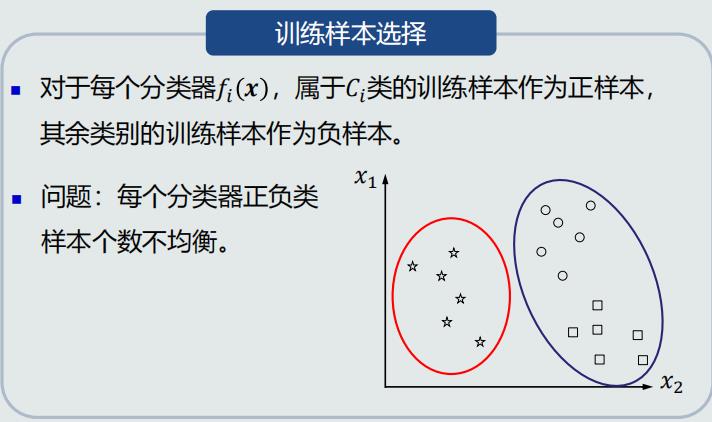
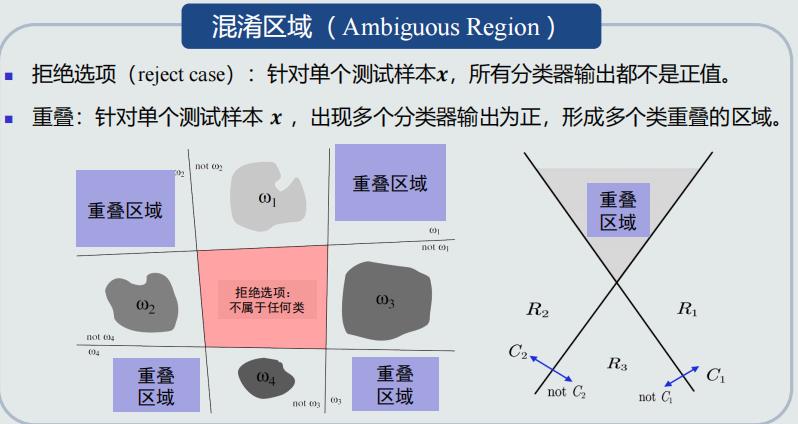
线性机




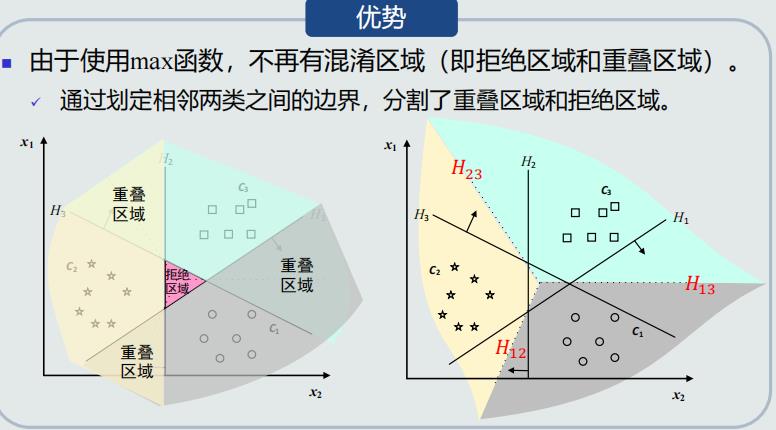
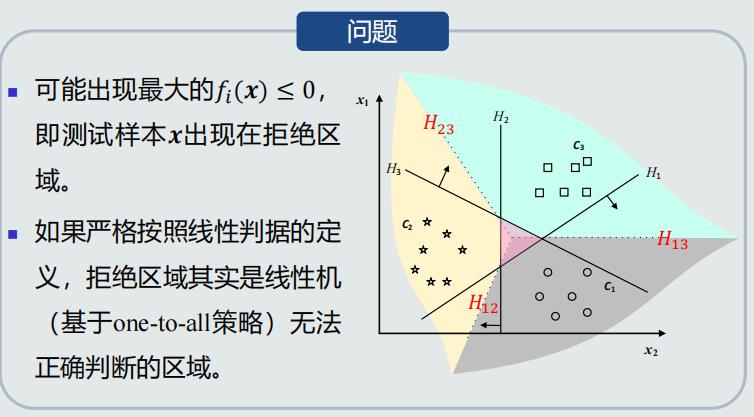
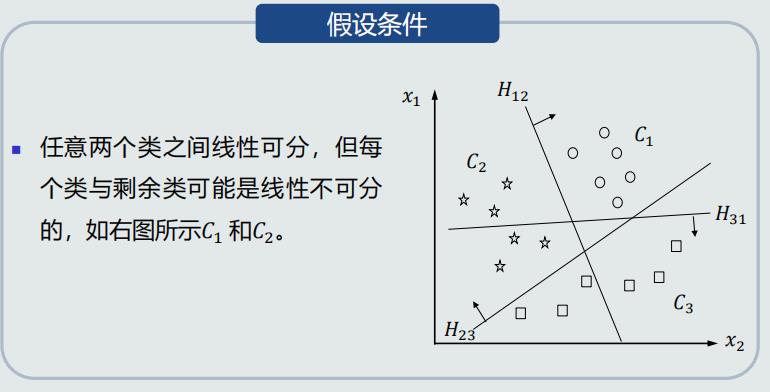
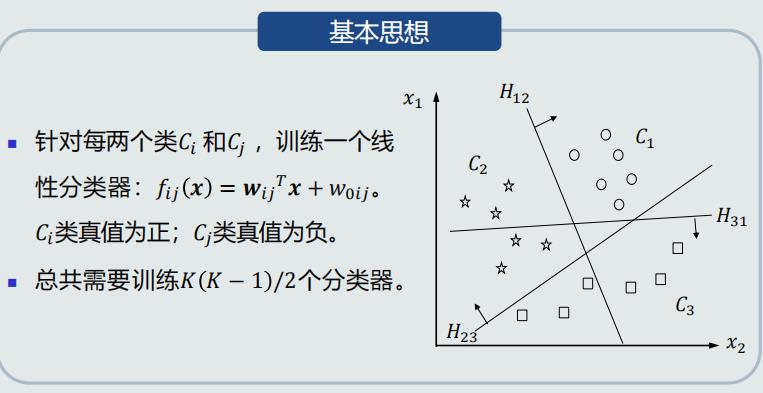
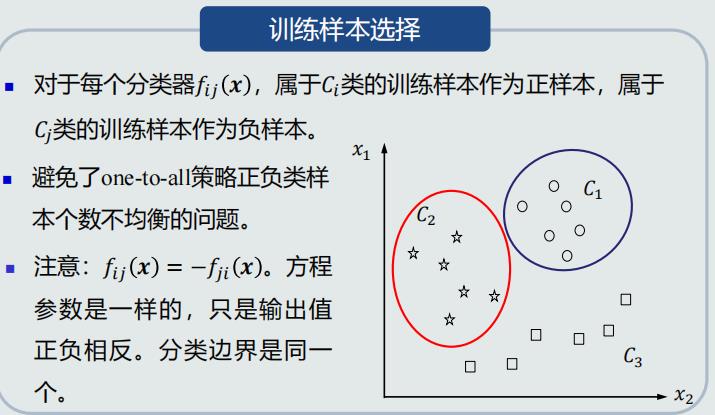
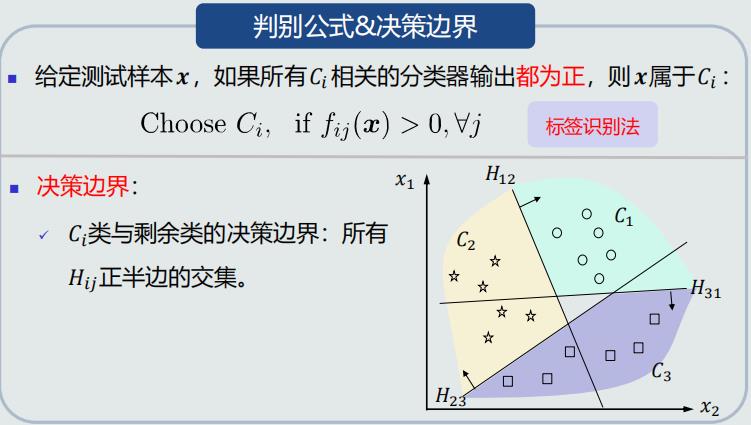
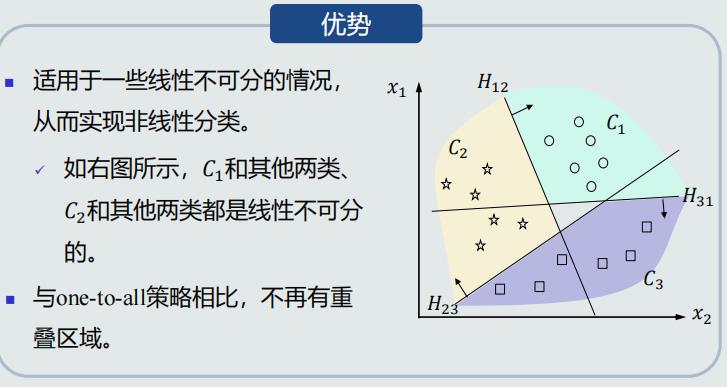
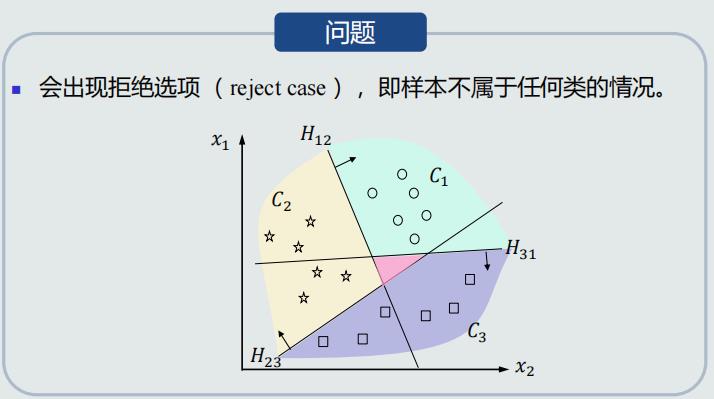
One-to-one策略

总结
- 使用线性判据进行多类分类,本质上是利用多个线性模型组合而成一个非线性分类器
- 因此,决策边界不再是由单个超平面决定,而是由多个超平面组合共同切割特征空间
4.12、 线性回归
输出数据
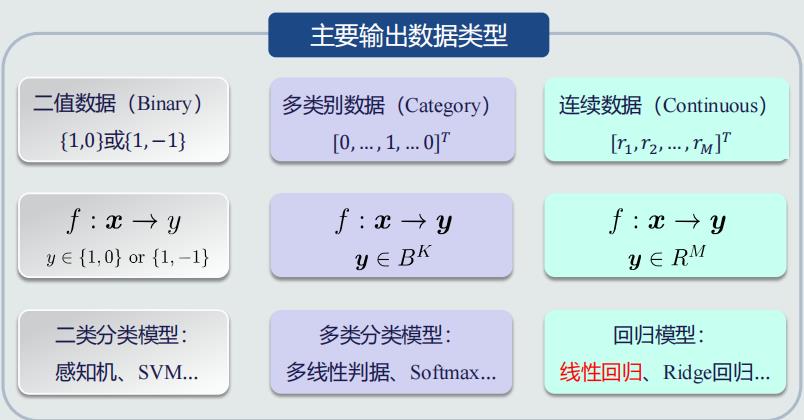
输入数据

线性回归模型表达


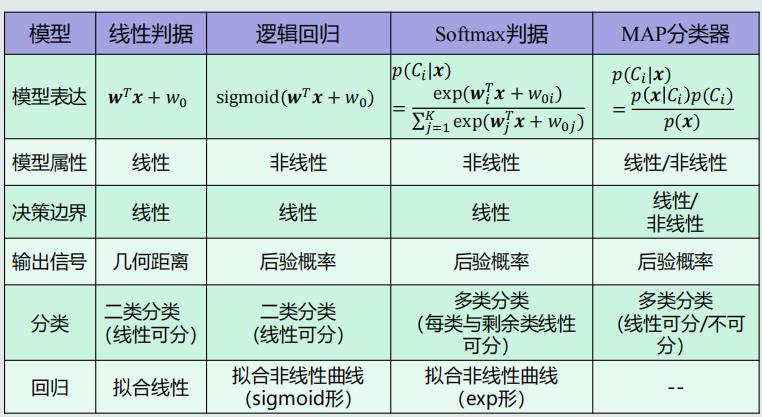
模型对比

训练样本

目标函数

- 线性判据:主要判断预测的输出值与真值在符号上的差异
- 感知机:被错误分类的样本的输出值之和。虽然输出值代表错误的程度,但是不考虑正确分类的正确程度
- 线性回归:比较预测的输出值和真值在数值上的差异
目标优化
- 梯度下降法

- 最小二乘法

似然函数


4.13、 逻辑回归的概念
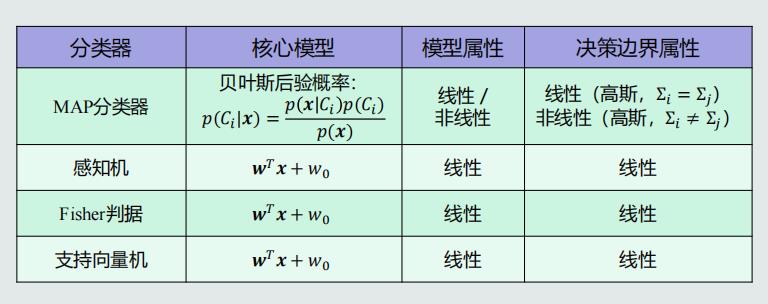
典型模型的属性
Logit变换

- Sigmoid函数:连接线性模型和后验概率的桥梁
- 线性模型𝑓(𝒙) + Sigmoid函数 = 后验概率
逻辑回归


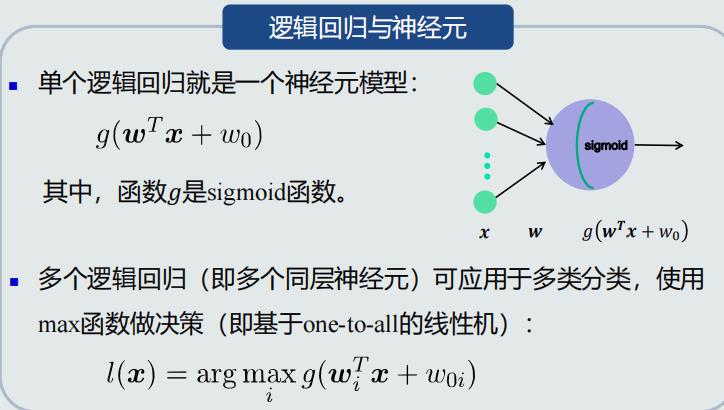

- 总结
- 逻辑回归本身是一个非线性模型
- 逻辑回归用于分类:仍然只能处理两个类别线性可分的情况。但是,sigmoid函数输出了后验概率,使得逻辑回归成为一个非线性模型。因此,逻辑回归比线性模型向前迈进了一步
- 逻辑回归用于拟合:可以拟合有限的非线性曲线
模型对比
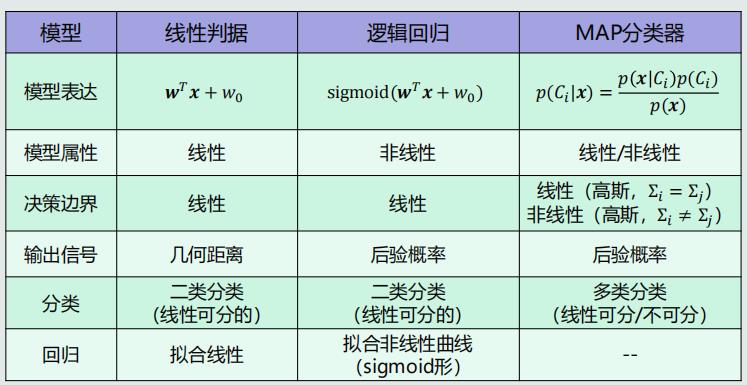
4.14、 逻辑回归的学习
最大似然估计法

训练目标
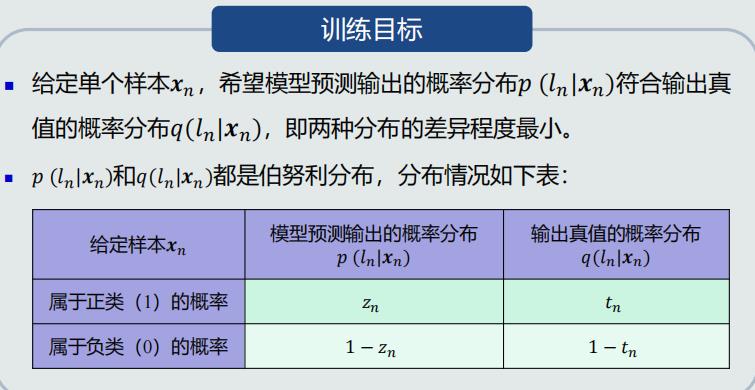
交叉熵

目标函数优化:梯度下降法
- 对参数𝒘求偏导
- 对参数𝑤0求偏导
- 参数更新
梯度消失问题

- 参数𝒘尽量选择较小的初始值,避免出现梯度消失问题
- 如果迭代停止条件设为训练误差为0,或者所有训练样本都正确分类的时候才停止,则会出现过拟合问题
- 在达到一定训练精度后,提前停止迭代,可以避免过拟合
- 迭代次数要达到一定程度,训练性能较好
- 逻辑回归输出的非线性形式就是sigmoid函数的非线性形式
4.15、 Softmax判据的概念
后验概率:多类情况

Softmax函数

Softmax判据

决策边界

Softmax判据与神经网络
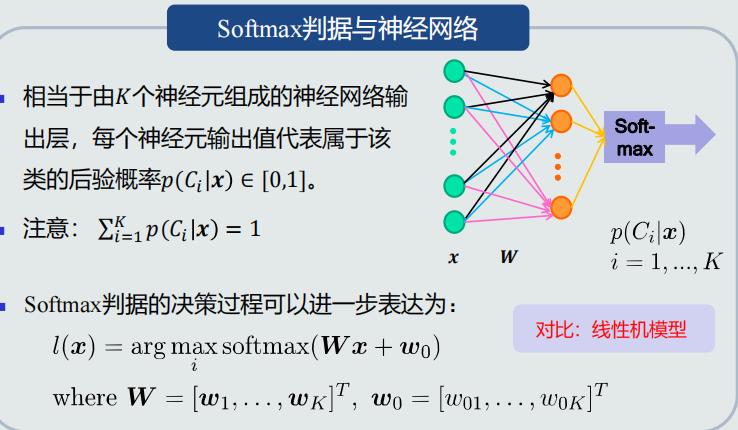
适用范围
- 适用范围:分类
- 前提:每个类和剩余类之间是线性可分的
- 适用范围:回归
- 范围:可以拟合指数函数(exp)形式的非线性曲线
总结
- Softmax判据本身是一个非线性模型
- Softmax判据用于分类:只能处理多个类别、每个类别与剩余类线 性可分的情况。但是, Softmax判据可以输出后验概率。因此,Softmax判据比基于one-to-all策略的线性机向前迈进了一步
- Softmax判据用于拟合:可以输出有限的非线性曲线
模型对比
4.16、Softmax判据的学习
目标函数:最大似然估计

目标函数:交叉熵解释
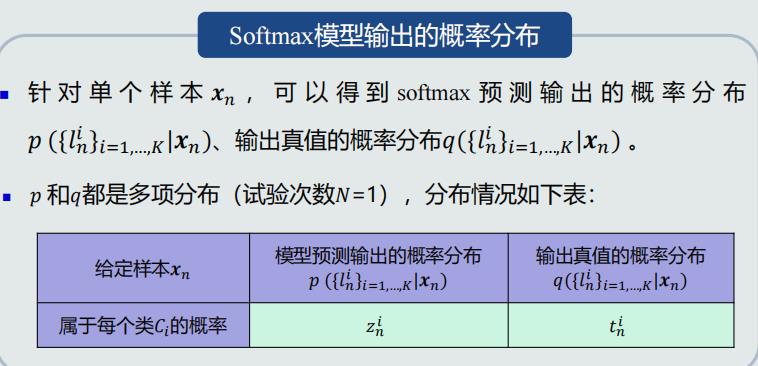

目标函数优化
- 对参数𝒘𝑘求偏导
- 对参数𝑤0𝑘求偏导
- 参数更新
梯度分析

梯度对比



