《机器学习》第一次作业——第一至三章学习记录和心得
《机器学习》第一次作业——第一至三章学习记录和心得
第一章 基本概念
1.1 什么是模式识别
模式识别:根据已有知识的表达,针对待识别模式,判别决策其所属的类别或者预测其对应的回归值
样本(Sample):一个具体的研究(客观)对象。如患者,某人写的一个汉字,一幅图片等
模式(Pattern):对客体(研究对象)特征的表述(定量的或结构的描述),是取自客观世界的某一样本的测量值的集合(或综合)
模式是样本的一种抽象。
怎么理解回归是分类的基础:样本要先经过回归器得到回归值,再送入分类器做分类
01模式识别的应用实例
-
计算机视觉领域
①手写体字符识别:OCR ②交通标志识别:辅助/无人驾驶 ③动作识别
-
人机交互领域
语音识别
-
医学领域
心跳异位搏动识别
-
网络领域
应用程序识别(基于TCP/IP流量)
-
金融领域
①银行信贷识别 ②股票价格预测
-
机器人领域
机械手目标抓取点位姿
-
无人车领域
无人驾驶
02模式识别的基本定义

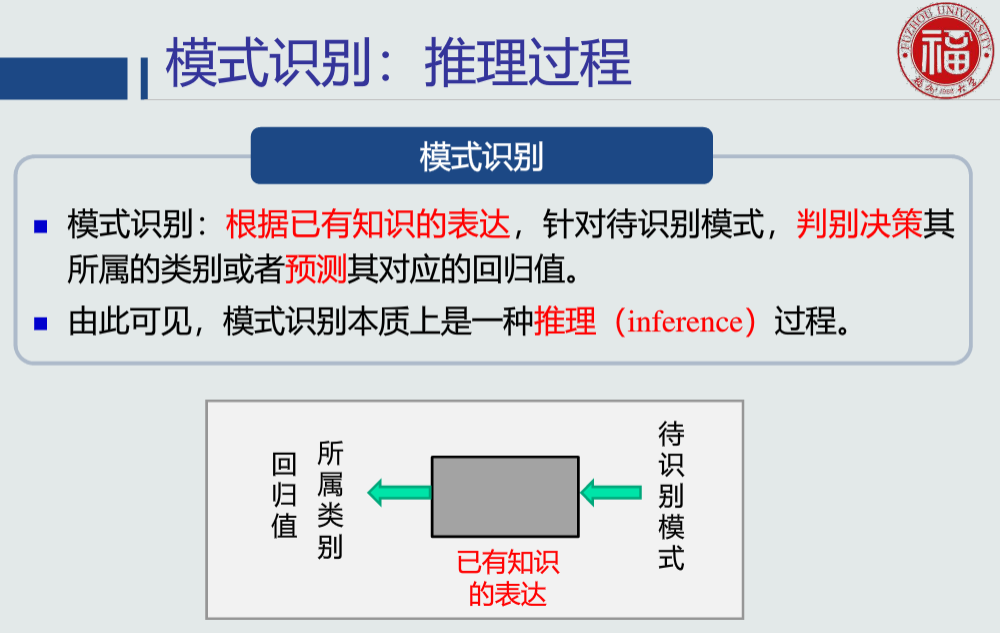
1.2模式识别数学表达

f(x):模型
可解析表达:可以用数学公式表达的模型
不能解析表达的模型:决策树、神经网络,深度学习
输入空间,输入的数据是:特征
一维:二类分类、回归值是一个值
并非特征的个数越多,模式识别的效果越准确,比如:过拟合
特征向量:由多个特征构成的(列)向量
为什么鲁棒性要好:针对不同的观测条件,仍能够有效表达类别之间的差异性
观测条件会影响样本数据,最终影响到性能
决策边界:用于分类,决策边界上,f(x)=0;决策边界可以是线、面、超平面
01模式识别数学解释

- 输入空间:原始输入数据x所在的空间
- 空间维度:输入数据的维度
- 输出空间:输出的类别/回归值y所在的空间
- 空间维度:1维、类别的个数(>2)、回归值的维度
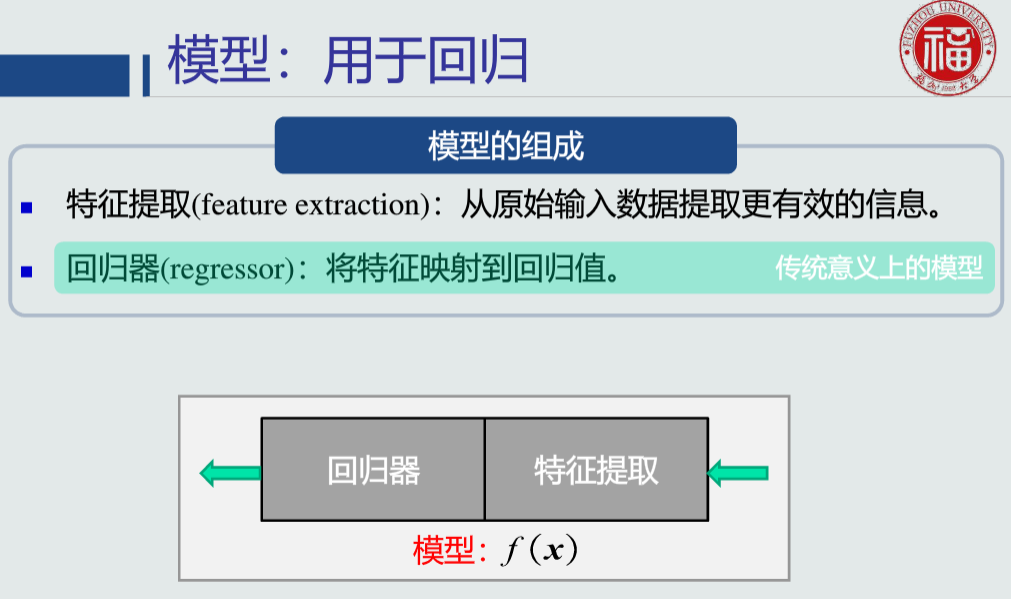
02模型的概念
模型:关于已有知识的一种表达方式,即函数f(x)
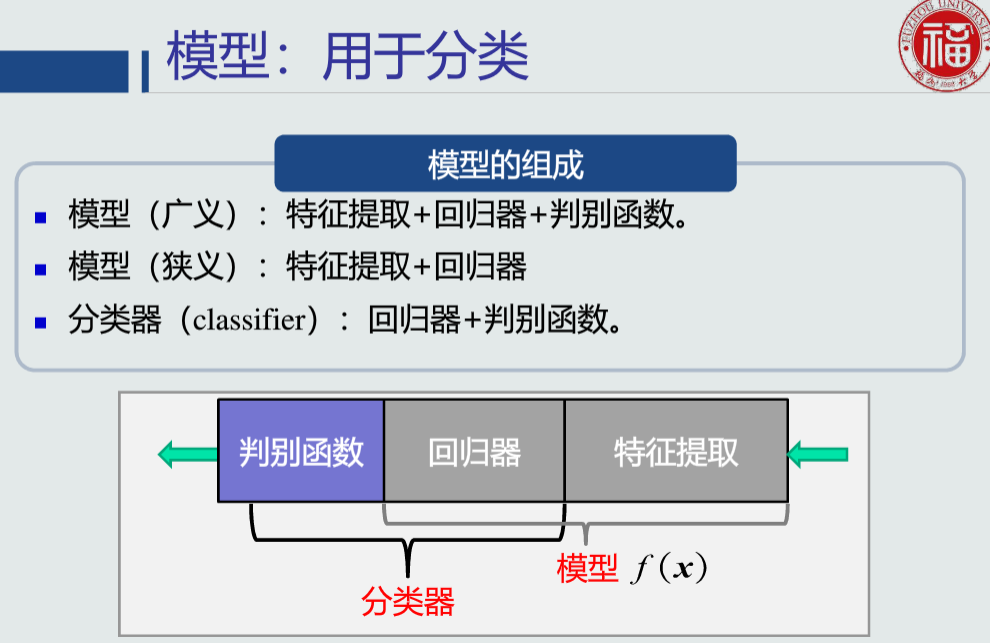
判别函数

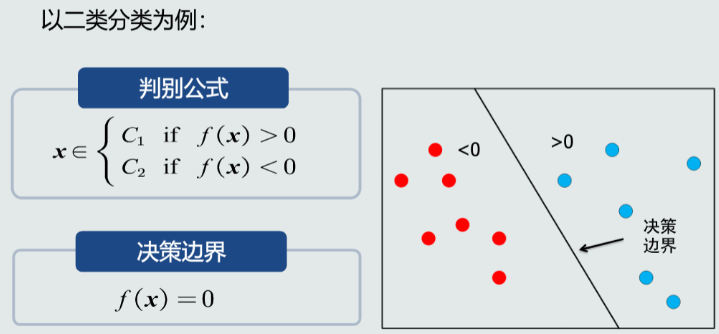
03特征&特征空间
特征:可以用于区别不同类别模式的、可测量的量
输入数据也可以看做是一种原始特征表达
特征(辨别能力):提升不同类别之间的识别性能(基于统计学规律、而非个例)
特征(鲁棒性):针对不同的观测条件,仍能够有效表达类别之间的差异性
特征向量

特征空间

1.3特征向量的相关性
特征向量的相关性的作用是:识别模式之间的相似度
点积的几何意义是:两个特征向量的共线性,即方向上的相似程度
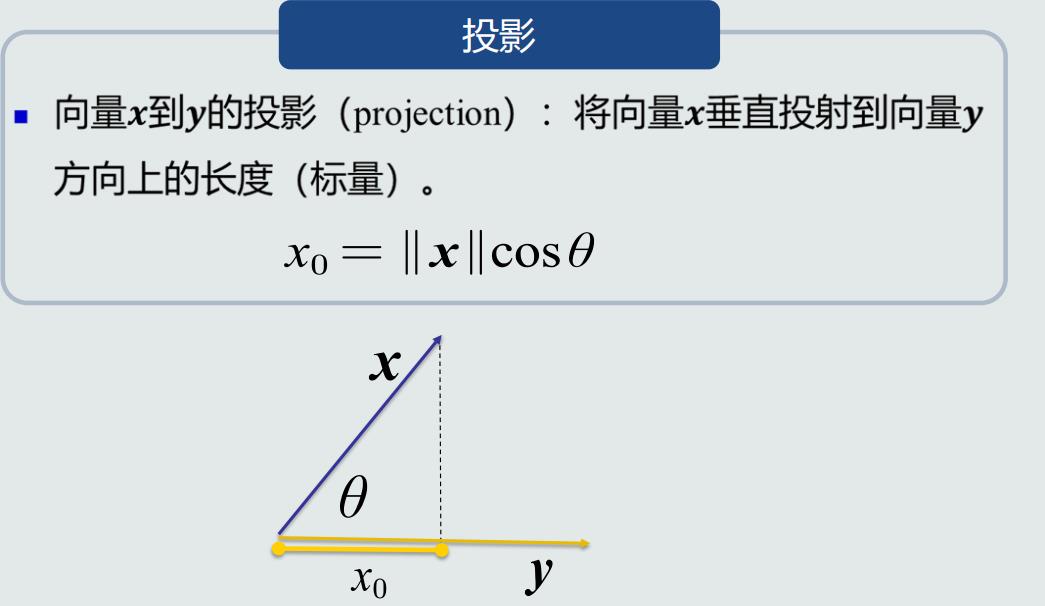
投影:向量x分解到y方向上的程度
点积和投影的区别是:点积具有对称性(x·y=y·x),投影不具有对称性
点积是不是考虑了2个向量的模长,投影只考虑了一个向量的模长;他们的本质区别,是在计算向量差异性的时候,衡量的方式不同
余弦定理,欧式距离,是常用的度量方式
特征向量点积:代数定义

特征向量点积:几何定义


特征向量投影

残差向量

欧氏距离

1.4机器学习基本概念
聚类技术用于图像分割的原理:属于同一个类别的像素分成一组
怎样算是 同类像素?颜色相似、纹理相似
机器学习算法为什么要设计目标函数?因为参数可能没有准确的解
什么情况下,参数可能没有准确解?over-determine under-determine
模式识别相当于机器学习好的系统,如何做决策推理的问题
机器学习解决给定一堆数据,如何设计、学习一个模型,并能够用于预测推理
训练样本可以认为是尚未加工的原始知识,模型则是经过学习(即加工整理归纳等)后的真正知识表达
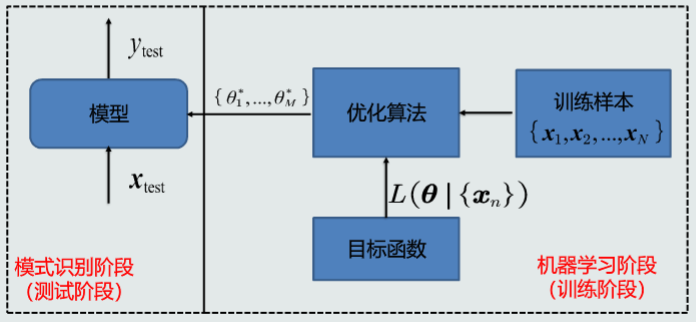
01模型如何得到
模型的参数和结构

线性模型

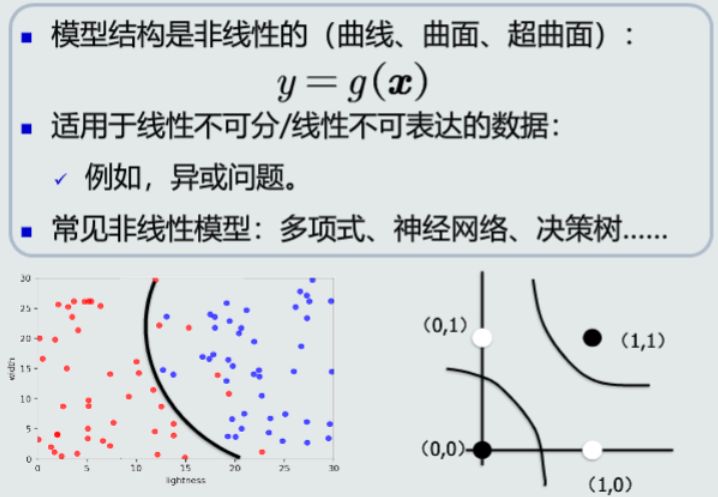
非线性模型
样本量VS模型参数量
N:训练样本个数 M:模型参数个数
- N=M:参数有唯一的解
- N>>M:没有准确的解
- N<<M:无数个解/无解
02机器学习的方式
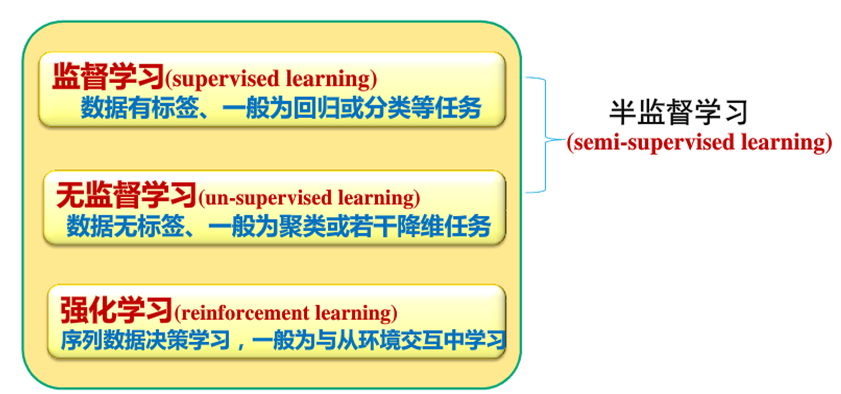
- 监督式学习:训练样本及其输出真值都给定情况下的机器学习算法。通常使用最小化训练误差作为目标函数进行优化。
- 无监督式学习:只给定训练样本、没有给输出真值情况下的机器学习算法。
- 半监督式学习:既有标注的训练样本、又有未标注的训练样本情况下的学习算法、
- 强化学习:机器自行探索决策、真值滞后反馈的过程。
1.5模型的泛化能力
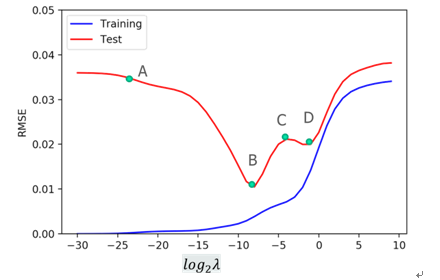
这个图中,哪个点的 泛化能力最好?B

左图过拟合,怎样避免或者是改进? 选择复杂度合适的模型或正则化
训练集和测试集的作用是什么?训练集训练模型,测试集评估模型

以多项式拟合为例,训练集 训练的参数是什么? w

超参数 的作用是什么?需要人为预先设置,同时影响学习性能和效果
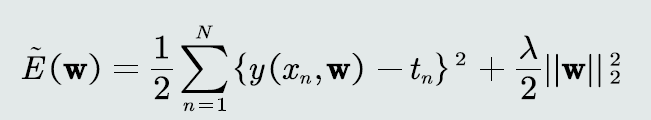
在损失函数中,加入后边的这个 2范数正则项的 作用是什么?调节正则系数,降低过拟合程度
还有训练集 训练模型参数,那么超参数用什么来训练?调参
正则项防止过拟合的作用,那为什么这项加进来就防止了过拟合?我们的模型训练时,不希望 w 达到太大;一般来说,模型过拟合的时候,曲线抖动比较大;在一定程度上,我们认为w也是比较大的;所以,我们这样考虑正则项。当然,这只是正则项中的一种设置,也是一个角度的考虑;在实际的应用中,正则项还有很多其他的构造方法
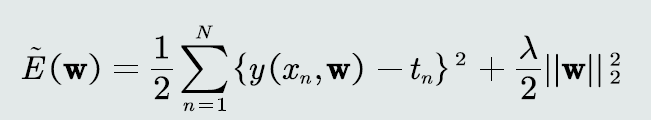
在这个式子里,为什么前后2项,都用了二分之一?方便求导计算
所以考虑到模型训练超参数调整评估模型,所以我们把数据集一般分作训练集、验证集、测试集
训练集&测试集

训练误差&测试误差

模型的泛化能力

过拟合
- 模型训练阶段表现很好,但是测试阶段表现很差
- 模型过于拟合训练数据
如何提高泛化能力
- 思路:不要过度训练
- 方法:
- 选择复杂度适合的模型:模型选择
- 正则化:在目标函数中加入正则项
1.6评估方法与性能指标
当数据集中,正例和反例比例差别比较大的时候,为什么会严重影响模型性能?f1-score不会很高
Accuracy = TP+TN/(TP+TN+FP+FN);
对于不平衡数据集,我们一般进行采样,让数据集正负平衡。
留一法有什么缺点? 计算开销大
留一法相当于k折交叉验证中,k为样本个数。那它的优点是什么?具有确定性,做多次实验结果一致;不像我们如果是用 k折交叉,多次实验的结果肯定会有偏差,因为 k折划分的数据集,是随机的;留一法也适用于小样本
但在实际的应用中,到底k折还是留一也没有一定的场景套用;并不是说 样本和特征 达到多少比例,用留一法
假设TP=10,FN=20;FP=5;TN=15召回率1/3,精度2/3,准确度1/2
对于k折交叉验证,k越大不一定越好,选择大的k会加大评估时间。这个说法对吗?对
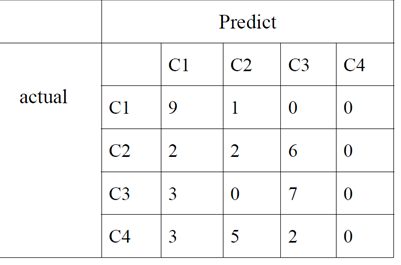
有这样一个模型的多类分类结果

算一下这个矩阵的精度,召回率
01评估方法
留出法

K折交叉验证

留一验证

02性能指标度量
基本概念
- 真阳性(TP),假阳性(FP),真阴性(TN),假阴性(FN)
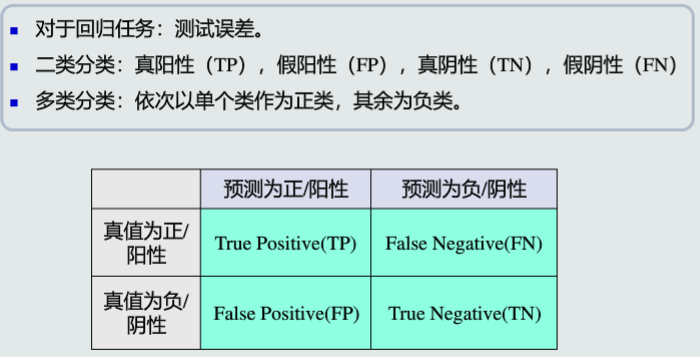
准确度
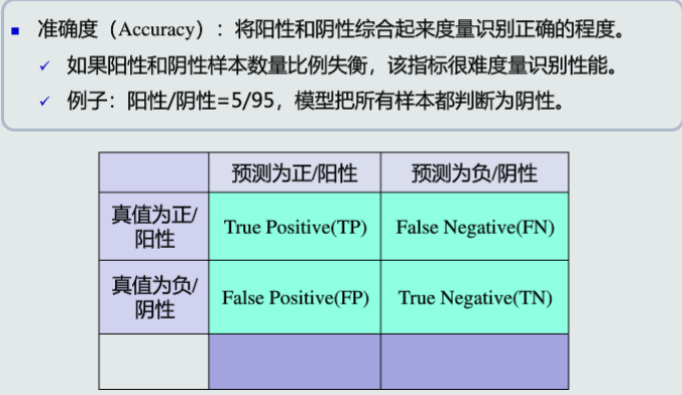
精度&召回率
精度:预测为阳性样本的准确程度。在信息检索领域,也称作查准率
召回率:也称作敏感度,全部阳性样本中被预测为阳性的比例。在信息检索领域也称作查全率
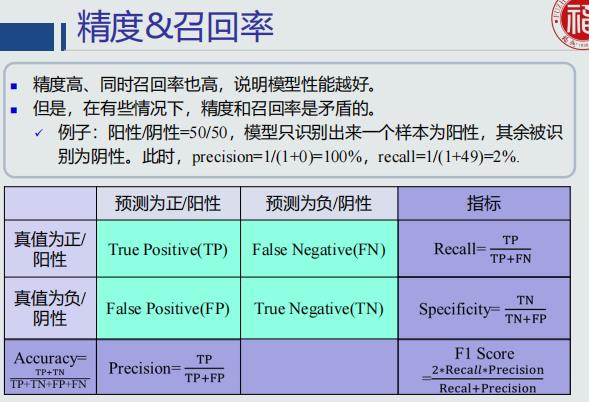
F-Score

混淆矩阵:矩阵的列代表预测值,行代表真值,对角线元素的值越大,表示模型性能越好。
PR曲线:横轴召回率,纵轴精度,PR曲线越往右上凸,说明模型的性能越好。
ROC曲线:横轴FPR,纵轴TPR,FPR=FP/(FP+TN),ROC曲线越往左上凸,说明模型的性能越好。
AUC:曲线下方面积
第二章
2.1MED分类器
01基于距离分类的基本概念
基于距离的决策:把测试样本到每个类之间的距离作为决策模型,将测试样本判定为与其距离最近的类
判别公式
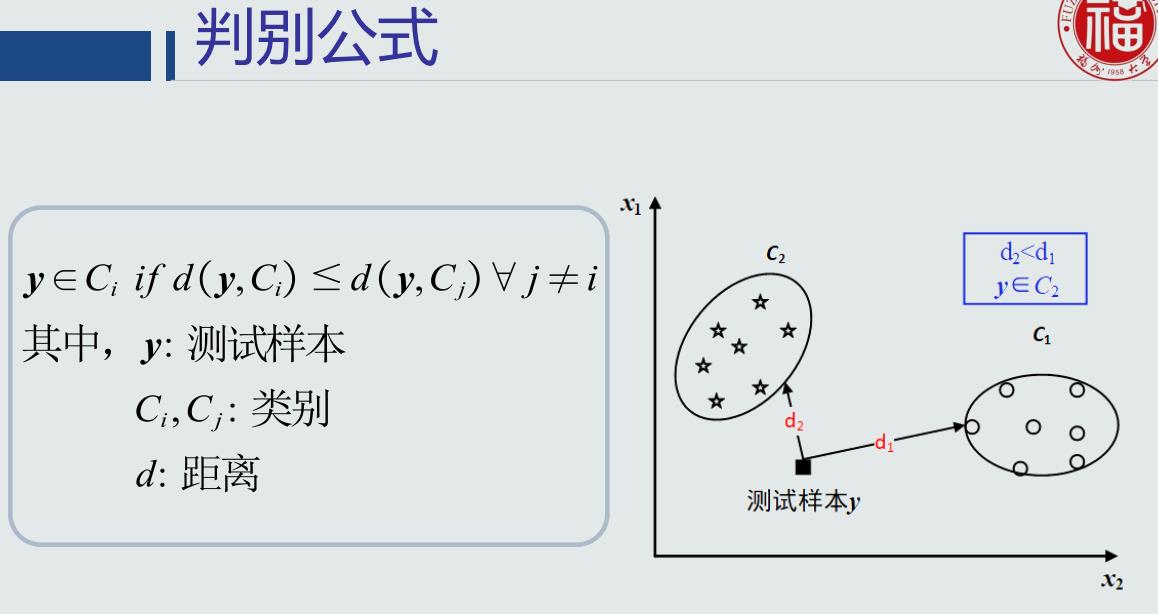
类的原型
- 均值:该类中所有训练样本的均值作为类的原型
- 最近邻:从一类的训练样本中,选取与测试样本距离最近的一个训练样本,作为该类的原型。类的原型取决于测试样本。
距离度量


02MED分类器
MED分类器:最小欧拉距离(Mininal Euclidean Distance)分类器,它选取类中样本均值作为类的原型,将待预测样本判断为与其欧拉距离最小的类
MED分类器的决策边界

在高维空间中,该决策边界是一个超平面,且该平面垂直且二分连接两个类原型的线
MED分类器的问题:没有考虑特征变化的不同及特征之间的相关性
- 对角线元素不相等:每维特征的变化不同
- 非对角线元素不为0:特征之间存在相关性
解决方法:去除特征变化的不同及特征之间的相关性
2.2特征白化
特征正交白化
- 目的:将原始特征映射到一个新的特征空间,使得在新空间中特征的协方差矩阵为单位矩阵,从而去除特征变化的不同及特征之间的相关性
- 将特征转换分为两步:先去除特征之间的相关性(解耦,Decoupling),然后再对特征进行尺度变换(白化,Whitening),使每维特征的方差相等。

特征向量与特征值



特征解耦


-
协方差矩阵的不同特征值对应的特征向量间一定正交
-
转换前后欧氏距离保持一致
特征白化
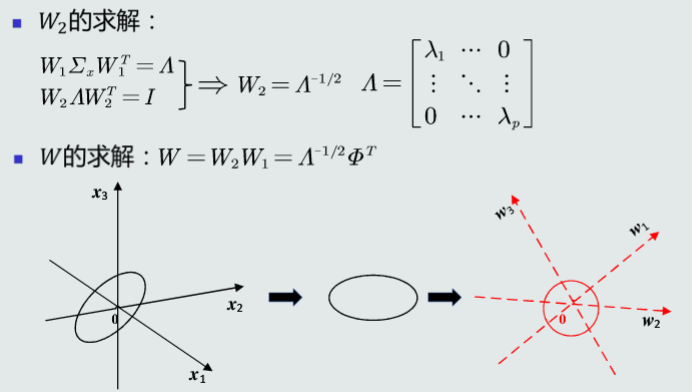

2.3MICD分类器
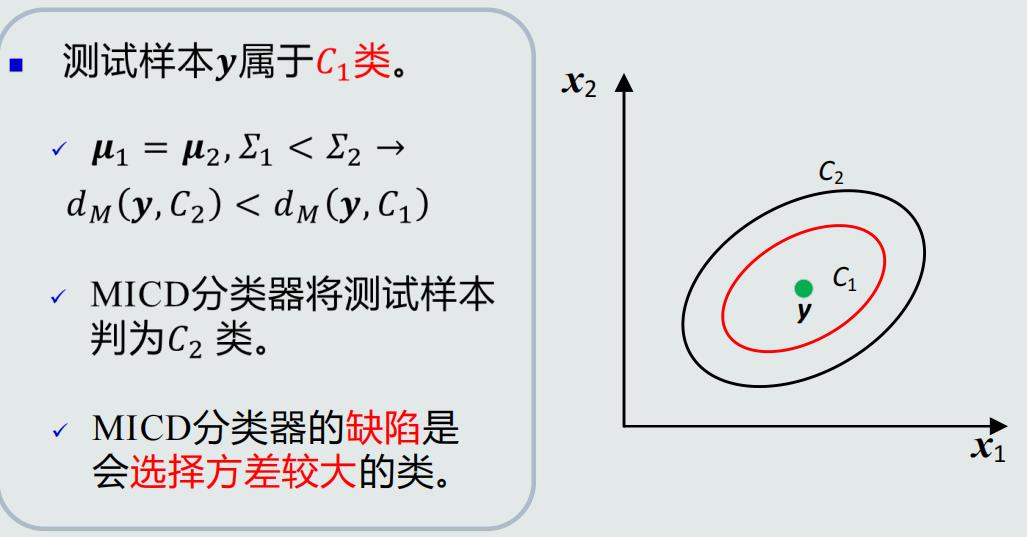
MICD分类器:最小类内距离(Minimal Intra-Class Distance)分类器由MED分类器演化而来,同样采用均值作为类的原型,但采用马氏距离作为距离度量。将待预测样本判断为与其马氏距离最小的类。
判别公式

马氏距离的属性
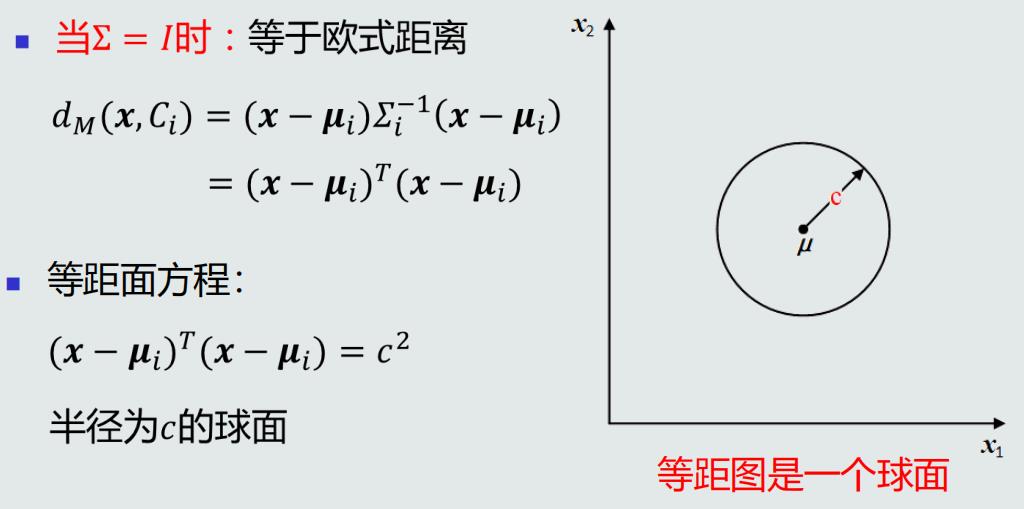
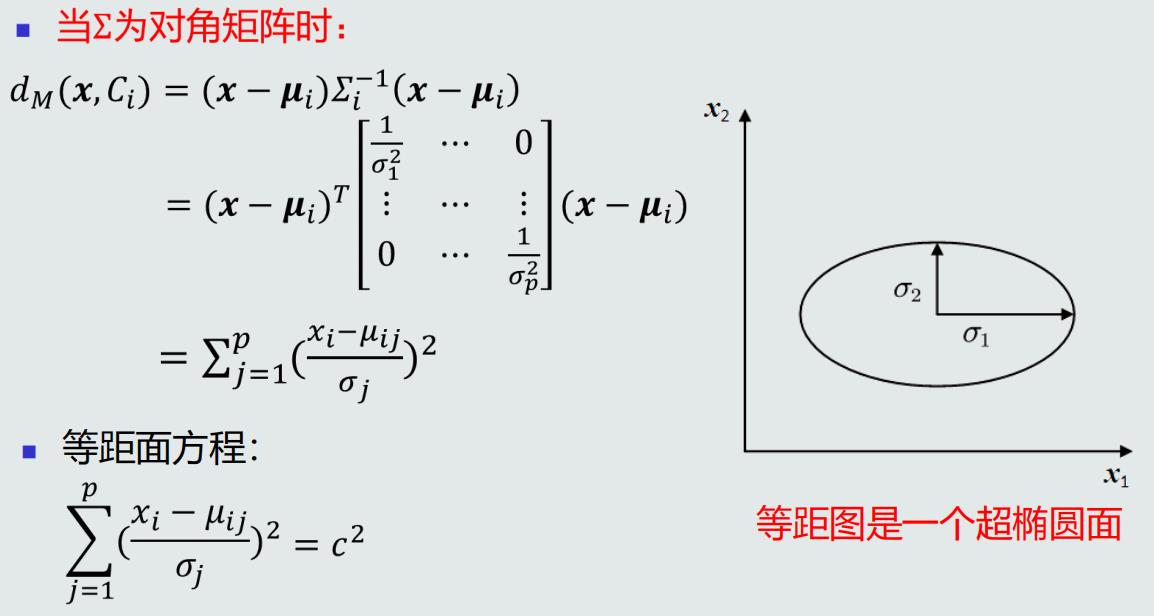

MICD分类器的决策边界


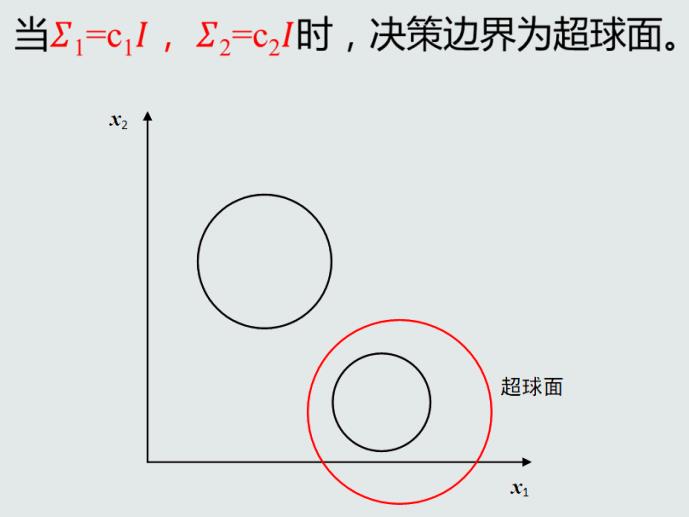
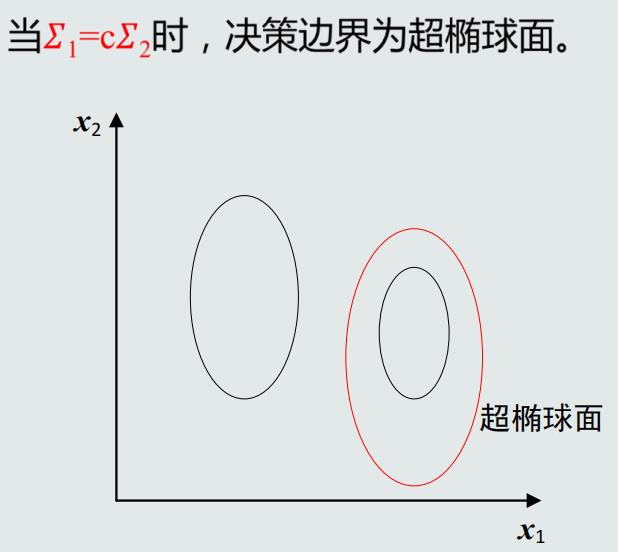
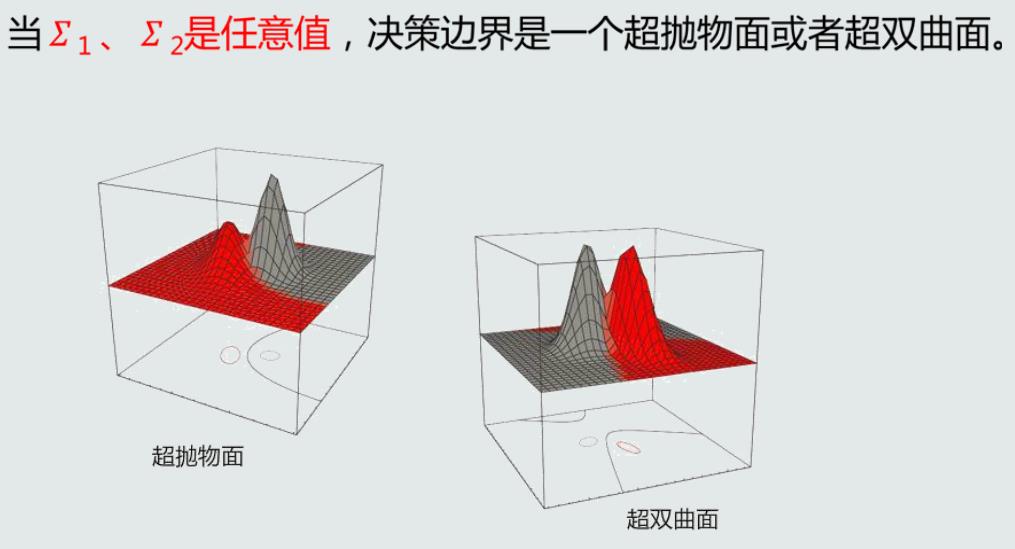
MICD分类器的问题
第三章
3.1贝叶斯决策与MAP分类器
基于距离的决策
- 仅考虑每个类别各自观测到的训练样本的分布情况,例如,均值(MED分类器)和协方差(MICD分类器)。
- 没有考虑类的分布等先验知识,例如,类别之间样本数量的比例,类别之间的相互关系。
概率的观点
- 随机性:每个样本是一次随机采样,样本个体具有随机性
- 概率:通常用来表达事物处于每种取值状态的可能性。
- 每维特征构成一个随机变量,其概率分布由两个元素组成:该特征的取值空间(连续或者离散)。在该特征维度上,样本处于各个取值状态的可能性。
后验概率:用于分类决策


贝叶斯规则

MAP分类器
MAP分类器:最大后验概率(Maximum posterior probability)分类器,基于贝叶斯规则,利用类的先验概率和观测似然概率,计算模式x属于类C的后验概率,进而进行分类判别
判别公式

决策边界

单维空间:通常有两条决策边界;高维空间:复杂的非线性边界。
决策误差
给定一个测试样本x,MAP分类决策产生的误差可以用概率误差表达
- 概率误差等于未选择的类所对应的后验概率
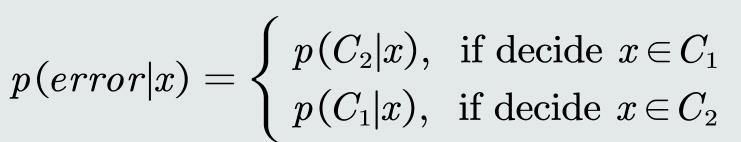
-
平均概率误差

决策误差最小化
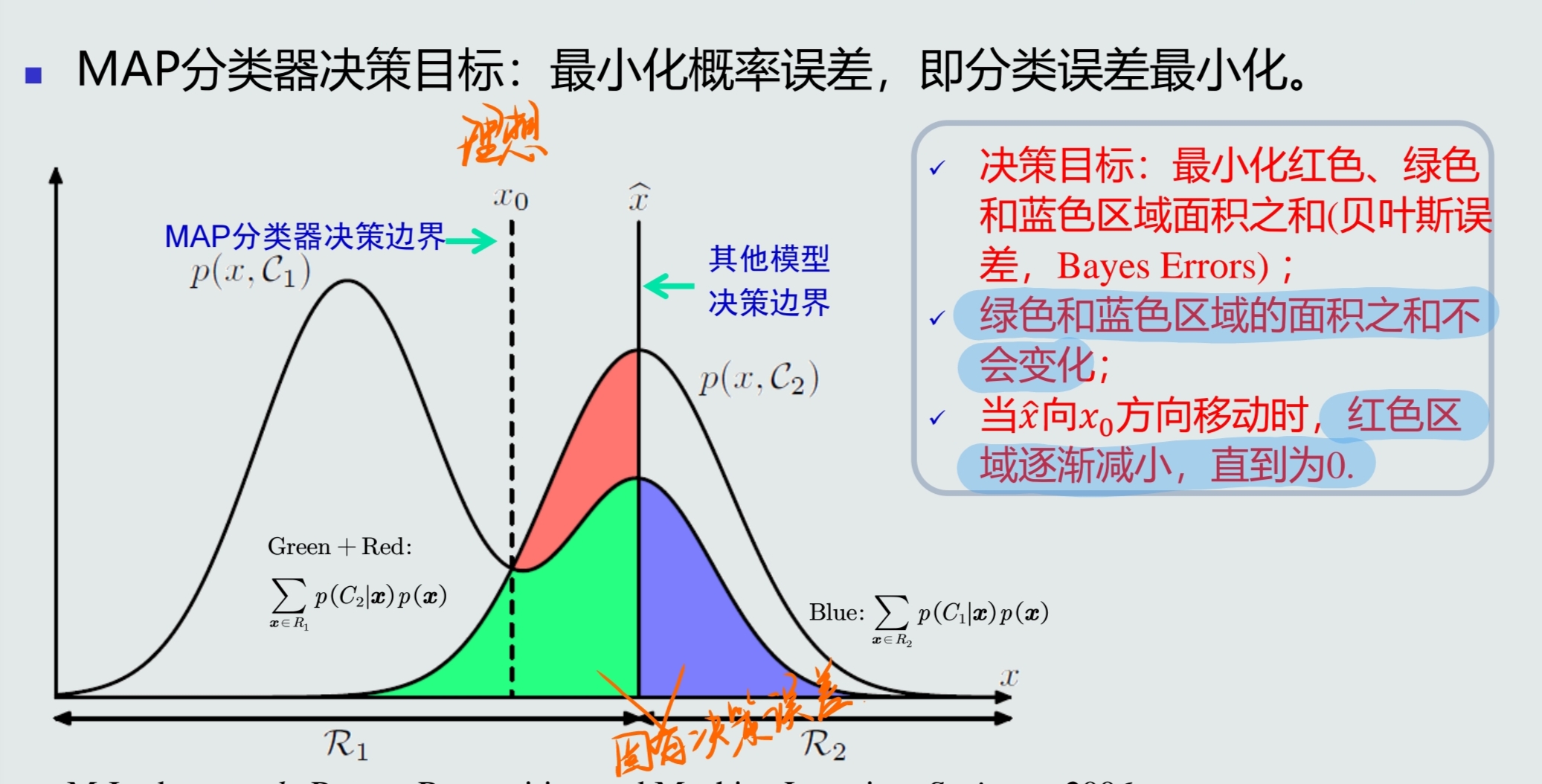
给定所有测试样本,MAP分类器选择后验概率最大的类,等于最小化平均概率误差,即最小化决策误差
3.2MAP分类器:高斯观测概率
先验和观测概率的表达
-
先验和观测概率的表达方式
-
常数表达:
\[p(Ci)=0.2 \] -
参数化解析表达:高斯分布……
-
非参数化表达:直方图、核密度、蒙特卡洛……
-
观测概率为单维高斯分布
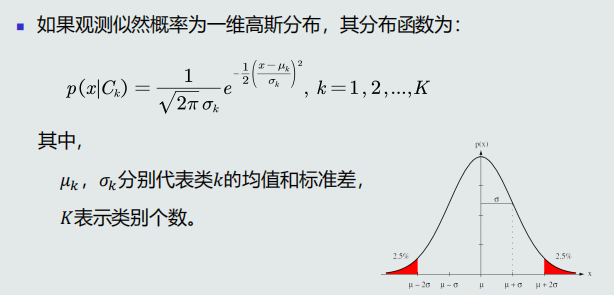

高斯观测概率:决策边界


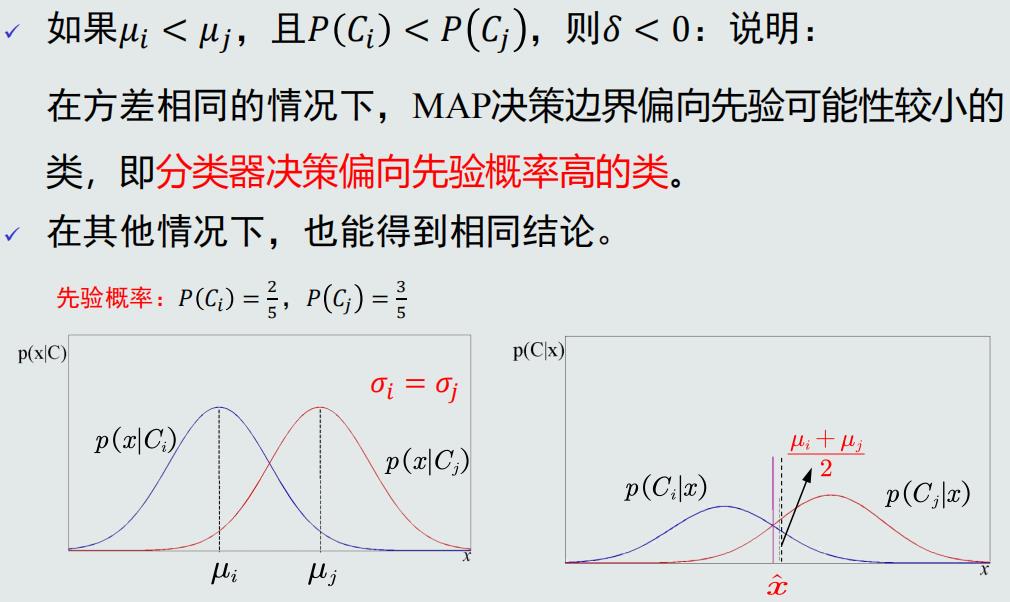

MAP分类器可以解决MICD分类器存在的问题

观测概率:高维高斯分布

3.3决策风险与贝叶斯分类器
-
决策风险:贝叶斯决策不能排除出现错误判断的情况,由此会带来决策风险。
-
损失:定义一个惩罚量,用来表征当前决策动作相对于其他候选类别的风险程度,即损失(loss)。假设该测试样本𝒙 的真值是属于Cj𝐶𝑗类,决策动作αi𝛼𝑖对应的损失可以表达为:
\[λ(αi|Cj)𝜆(𝛼𝑖|𝐶𝑗) \]简写为
\[λij \] -
损失的评估:针对所有决策动作和候选类别,可以用一个矩阵来表示对应的损失值
-
决策风险的评估:给定一个测试样本x,分类器决策其属于Ci类的动作αi对应的决策风险可以定义为相对于所有候选类别的期望损失,记作
\[R(αi|x)=∑jλijp(Cj|x) \] -
贝叶斯分类器:在MAP分类器基础上,加入决策风险因素,得到贝叶斯分类器(给定一个测试样本𝒙,贝叶斯分类器选择决策风险最小的类)
-
判别公式:

贝叶斯分类器:决策损失

贝叶斯分类器:决策目标
-
给定所有测试样本 {𝒙},贝叶斯分类器的决策目标:最小化期望损失
-
如何实现期望损失最小化?对每个测试样本选择风险最小的类。

朴素贝叶斯分类器
-
背景:如果特征是多维,学习特征之间的相关性会很困难。
-
假设特征之间是独立的:
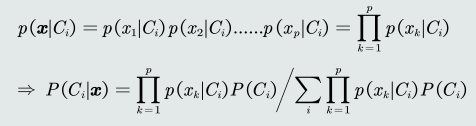
-
为了避免出现错误的决策,分类器可以选择拒绝。可以引入阈值τ。当τ=1时所有样本的任何决策都会被拒绝。当τ<1/k时,所有样本的决策都不会被拒绝,k是类别的个数。
3.4最大似然估计
监督式学习方法
- 参数化方法:给定概率分布的解析表达,学习这些解析表达函数中的参数。该类方法也称为参数估计。
- 例如,高斯分布的均值(向量)和方差(协方差)。
- 非参数化方法:概率密度函数形式未知,基于概率密度估计技术,估计非参数化的概率密度表达。
最大似然估计

先验概率估计
目标函数:给定所有类的𝑁个训练样本,假设随机抽取其中一个样本属于𝐶1类的概率为𝑃,则选取到𝑁1个属于𝐶1类样本的概率为先验概率的似然函数(即目标函数)。
该似然函数是二项分布(其中P是待学习的参数):
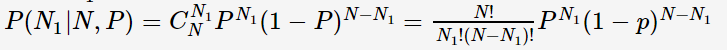

观测概率估计:高斯分布
-
待学习的参数:如果观测似然概率服从高斯分布,待学习的参数包含该高斯分布的均值𝝁和协方差𝚺。(观测似然概率是关于单个类的条件概率)
-
目标函数
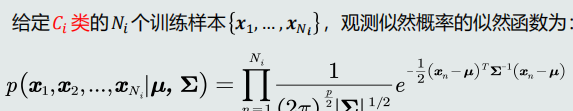
-
高斯分布参数估计

-
均值估计:高斯分布均值的最大似然估计等于样本的均值

-
协方差估计:高斯分布协方差的最大似然估计等于所有训练模式的协方差

3.5最大似然的估计偏差
无偏估计
- 如果一个参数的估计量的数学期望是该参数的真值,则该估计量称作无偏估计
- 无偏估计意味着只要训练样本个数足够多,该估计值就是参数的真实值
- 均值的最大似然估计是无偏估计
高斯分布协方差的最大似然估计是有偏估计



协方差估计的修正:在实际计算中,可以通过将训练样本的协方差乘以𝑁/(𝑁 − 1)来修正协方差的估计值
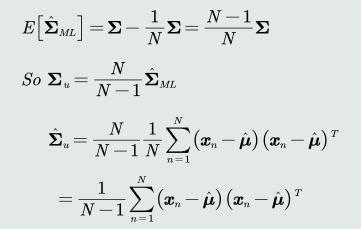
3.6贝叶斯估计(1)
- 概率分布中待学习的参数𝜃也可以当做随机变量。
- 贝叶斯估计:给定参数𝜃分布的先验概率以及训练样本,估计参数θ分布的后验概率。
- 假设𝜃服从一个概率分布:
- 该概率分布的先验概率已知:𝑝(𝜃)
- 先验概率反映了关于参数𝜃的最初猜测及其不确定信息
贝叶斯估计:概念

贝叶斯估计:高斯观测似然

参数(高斯均值)的后验概率

参数(高斯均值)的后验概率

- 给定𝐶𝑖类的𝑁𝑖个训练样本,参数θ概率分布的均值等于训练样本均值和该参数先验概率均值的加权和。
- 给定𝐶𝑖类的𝑁𝑖个训练样本,参数θ概率分布的方差是由𝐶𝑖类观测似然分布的方差、该参数的先验概率方差、𝐶𝑖类的样本个数共同决定。
- 当𝑁𝑖足够大时,样本均值m就是参数θ的无偏估计。
参数先验对后验的影响

贝叶斯估计:不断学习能力
- 它允许最初的、基于少量训练样本的、不太准的估计
- 随着训练样本的不断增加,可以串行的不断修正参数的估计值,从而达到该参数的期望真值
3.7贝叶斯估计(2)
贝叶斯估计流程步骤

3.8无参数概率密度估计(1)
- 常用的无参数技术:K近邻法、直方图技术、核密度估计
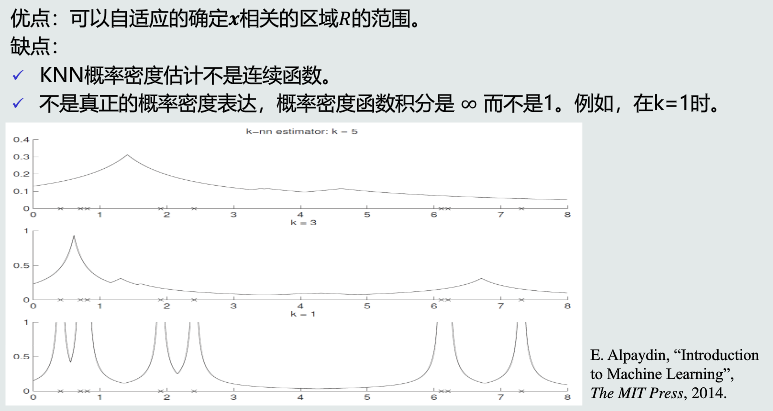
KNN估计

优缺点
3.9直方图与核密度估计
直方图估计
-
原理


-
优缺点

核密度估计
-
原理



-
优缺点



