从零开始手撸红黑树（三）

上节回顾

上节内容我们学习了自平衡二叉搜索树AVL树，在算出影响平衡的节点后，通过左旋和右旋的组合，使得整个二叉树的左右子树的高度差不大于1；

这节内容就来到了这个系列的关键点了，红黑树的相关内容；

红黑树

红黑树也是一种自平衡的二叉搜索树（以前名为平衡二叉B树）

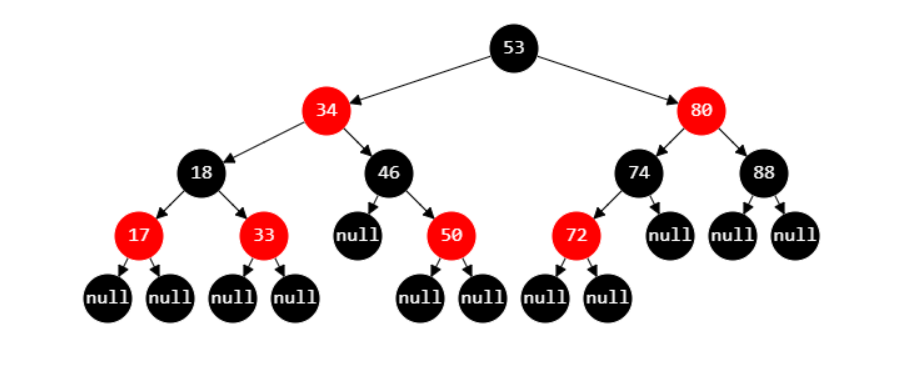
红黑树必须满足5条性质

  1. 节点是 RED 或者 BLACK
  2. 根节点是BLACK
  3. 叶子节点（外部节点，空节点）都是 BLACK
    • 红黑树的节点的度都为2，为满足这个性质，红黑树需要补全叶子节点中度不为2的节点。补全方式很简单，对每个度不为2的节点添加一个空的黑节点，如上图中节点数据为null的节点。
  4. RED 节点的 子节点 都是 BLACK
    • 由这个性质可以推断出如下的规则
    • RED 节点的 parent 都是 BLACK
    • 从根节点到叶子节点的所有路径上不能有 2 个连续的 RED 节点
  5. 从任一节点到叶子节点的所有路径都包含相同数目的 BLACK 节点

从这些性质上看很难理解为什么满足这些性质的树就是平衡的。红黑树之前的名字叫平衡二叉B树。大家都知道只有起错的名字，没有叫错的外号。那红黑树和B树又有什么关系呢。所以在深入学习红黑树之前，我们先学习一下B 树，现在先忘记上面的红黑树性质，进行B树的学习；

B树（B-tree， B-树）

B树： 一种平衡的多路搜索树，多用于文件系统，数据库的实现。



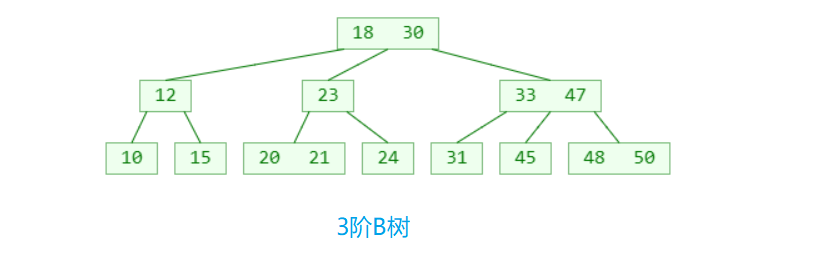
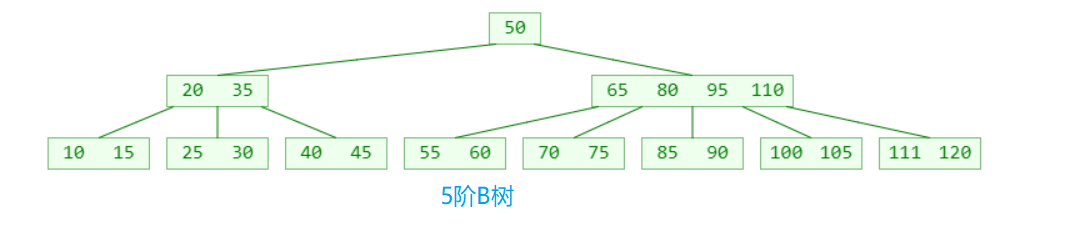
可以看出 B 树有以下特点

  1. 1个节点可以存储超过2个元素，可以拥有超过2个子节点
  2. 拥有二叉搜索树的一些性质
  3. 平衡，每个节点的所有子树高度一致
  4. 比较矮

m阶B树的性质（m>=2）

  1. 每个节点最多只有m个子节点
  2. 每个非叶节点（根节点除外）至少具有 ⌈m/2⌉  个子节点。 （ ⌈ -> 向上取整 ）
  3. 如果根不是叶节点，则根至少有两个子节点
  4. 一个有k个子节点的非叶子节点包含k − 1个元素
  5. 所有叶子都出现在同一层。

由上面的性质可以推断出一下结论

假设一个节点存储的元素个数为x

  1. 根节点 ： 1<= x <= m-1 （性质1，4）
  2. 非根节点：⌈m/2⌉ - 1 <= x <=m-1 （性质1，2，4）

假设一个子节点的个数为y

  1. 根节点上的子节点数： 2<= y <= m （性质1，3）
  2. 非根节点上的子节点数： ⌈m/2⌉ <= y <= m （性质1，2）

比如 m = 3时， 2<=y<=3 因此可以称为（2,3）树，2-3树
比如 m = 4时， 2<=y<=4 因此可以称为（2,3,4）树，2-3-4树

B树VS二叉搜索树

B树和二叉搜索树在逻辑上是等价的

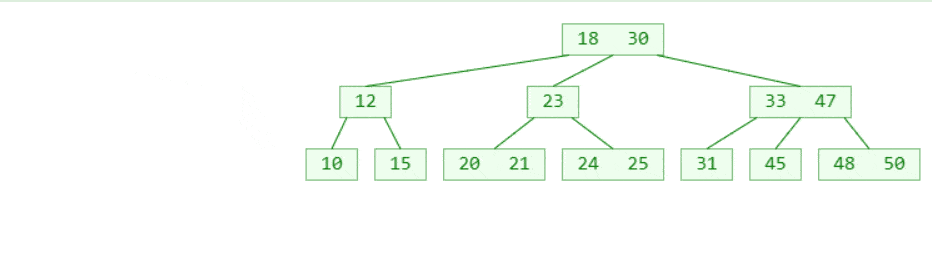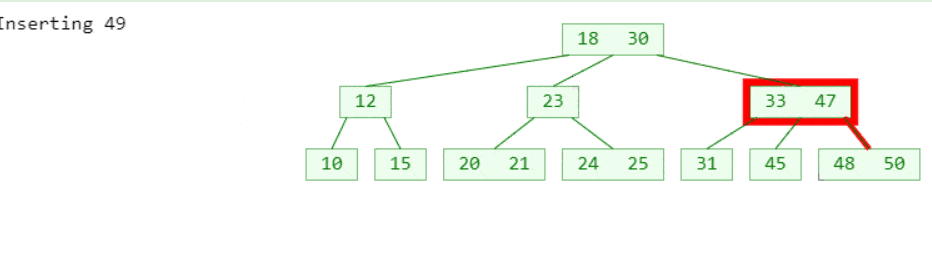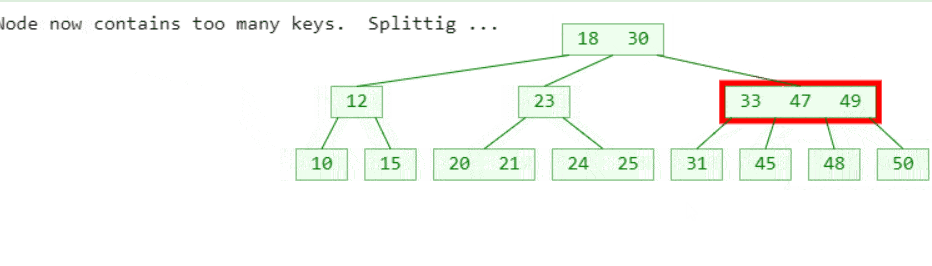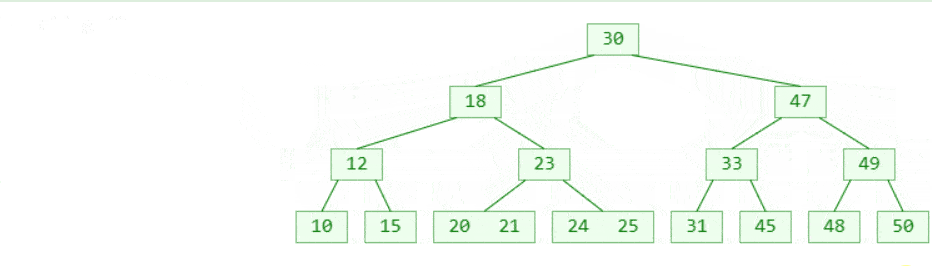
如下图，当把二叉搜索树的（18,33）节点合并，（23,30）节点合并，（20.21）节点合并，（45,47）节点合并，图1的二叉搜索树就是图2所展示的3阶B树。

图1

图2

当二叉树搜索树的多代节点合并，就是B树中存储多个元素的超级节点。

  • 2代合并的超级节点，最多拥有4个子节点
  • 3代合并的超级节点，最多拥有8个子节点
  • n代合并的超级节点，最多拥有2^n个子节点

m阶B树，最多需要log_2^m代合并

搜索

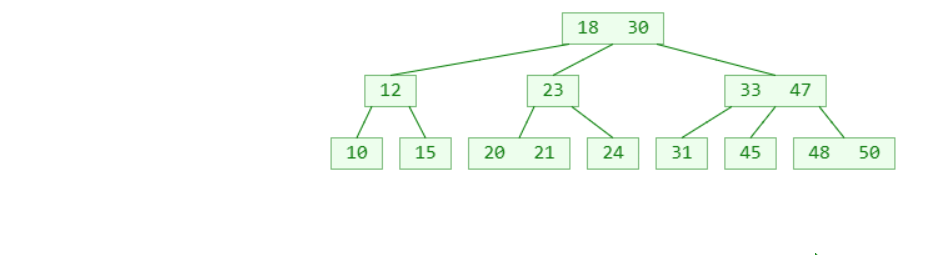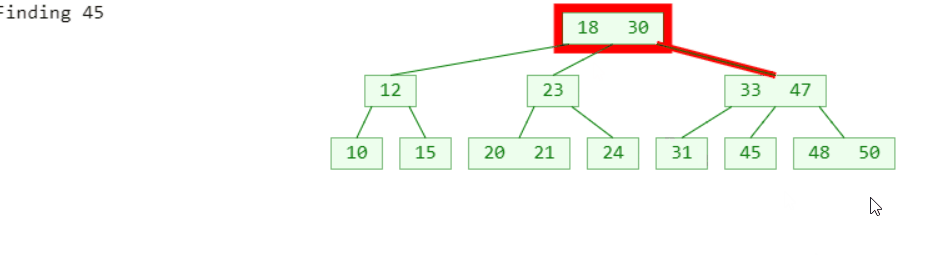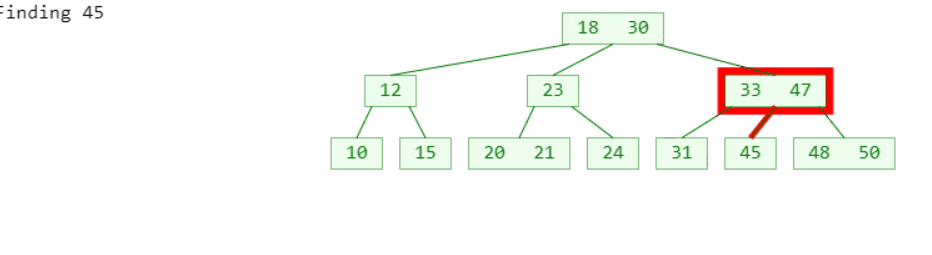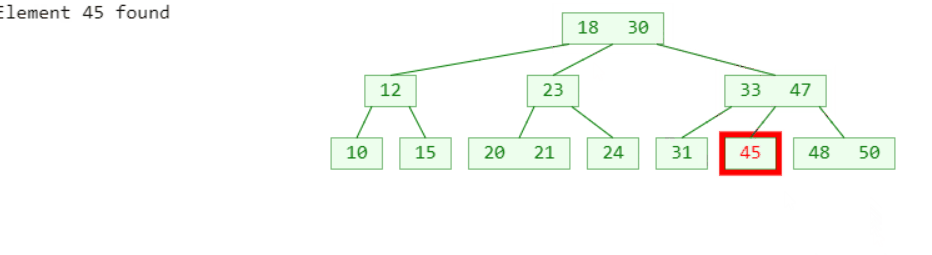
既然B树的逻辑和二叉搜索树是等价的，那搜索的逻辑其实也就差不多了

  1. 先在节点内部从小到大开始搜索元素
  2. 如果命中，搜索结束
  3. 如果未命中，再去对应的子节点中搜索元素，重复步骤 1

添加

新添加的元素必定是添加到叶子节点，和二叉搜索的添加类似。不同的是B树的一个节点可以存储多个元素。但是节点中可以存储的元素个数是有限制的，具体查看上文中的m阶B树的性质

这里分别有2个3 阶 B 树的添加例子，对应了B树添加的2种情况，3 阶 B 树的节点中元素的最大个数为 m-1=2

  1. 如果节点拥有的元素数量小于最大值，那么有空间容纳新的元素。将新元素插入到这一节点，且保持节点中元素有序。
  2. 否则的话这一节点已经满了，将它平均地分裂成两个节点
    1. 从该节点的原有元素和新的元素中选择出中位数
    2. 小于这一中位数的元素放入左边节点，大于这一中位数的元素放入右边节点，中位数作为分隔值。
    3. 分隔值被插入到父节点中，这可能会造成父节点分裂，分裂父节点时可能又会使它的父节点分裂，以此类推。如果没有父节点（这一节点是根节点），就创建一个新的根节点（增加了树的高度）。

删除

删除非叶子节点中的元素

删除非叶子节点和平衡二叉树的删除度为2的节点的方式是一致的

  1. 先找到删除节点的前驱或者后继元素，覆盖所需删除元素的值。非叶子节点的元素必定在叶子节点中
  2. 再把前驱或后继元素删除

删除叶子节点中元素

直接在所在节点中删除改元素

删除-下溢的解决

以上2中情况真正被删除的元素都是在叶子节点中，在删除叶子节点中的元素后，可能会出现删除后的节点中的元素的个数不满足 B 树的性质，即元素的个数小于该节点应该存放元素的最小值 ⌈m/2⌉ -1，这个情况叫（下溢）

如下图5阶B树中删除非叶子节点

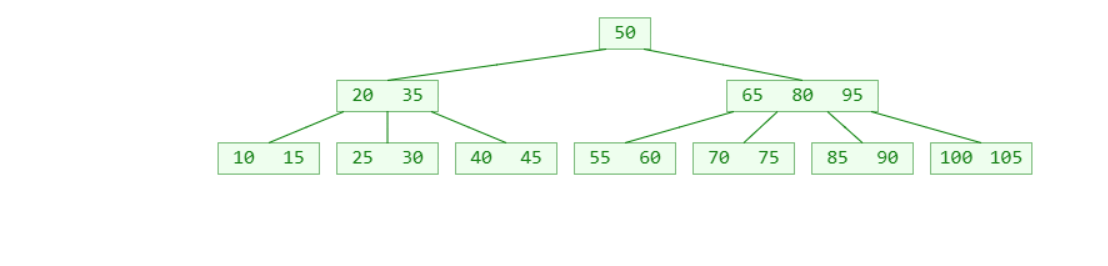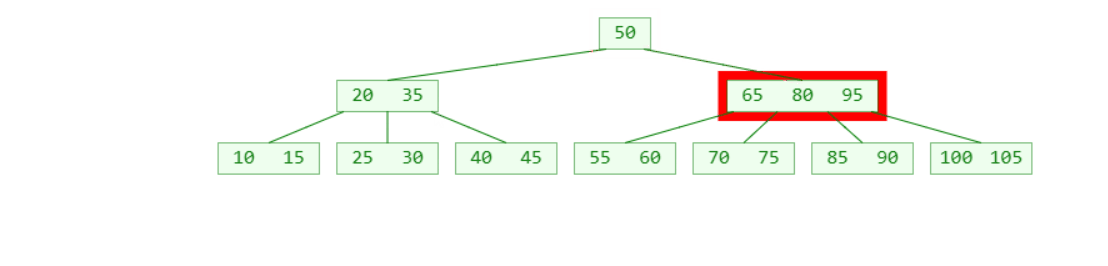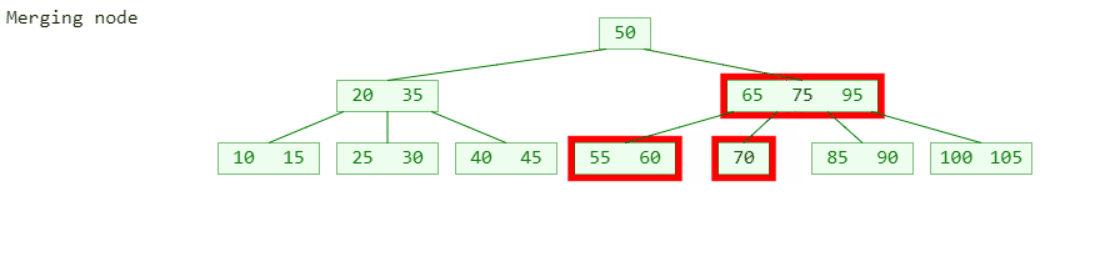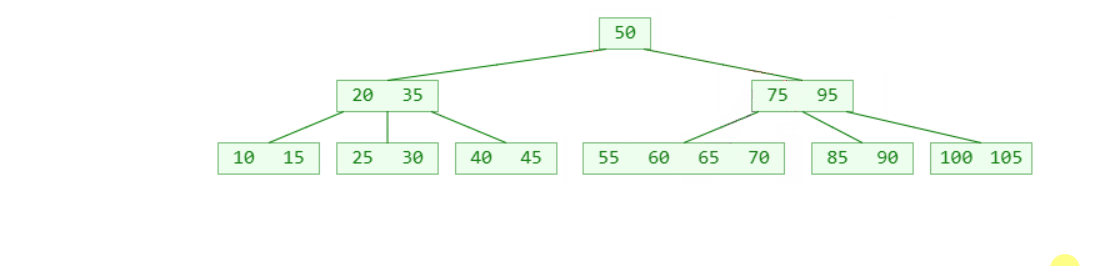
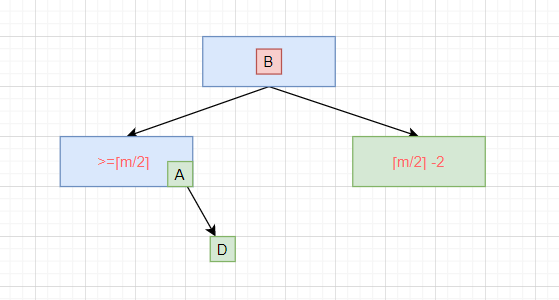
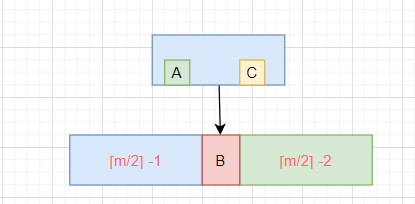
  • 根据m阶B树的性质，下溢节点的元素数量必然等于 ⌈m/2⌉ - 2
  1. 如上图，如果下溢节点临近的兄弟节点有至少 ⌈m/2⌉ 个元素，可以向其借一个元素
    1. 将父节点的元素B插入到下溢节点的最小位置
    2. 将元素A插入到父节点中


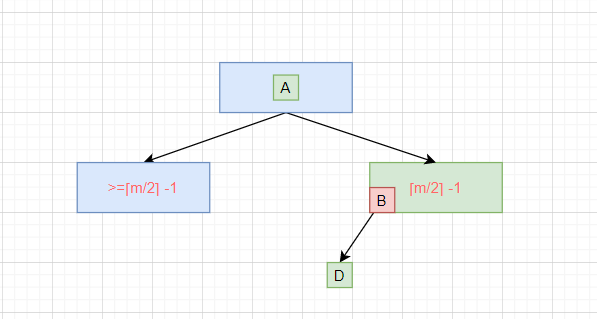
这种操作就是旋转

  1. 如果下溢节点的临近的兄弟节点只有 ⌈m/2⌉ -1个元素
    1. 它与一个直接兄弟节点以及父节点中它们的分隔值合并
    2. 合并后的节点元素个数等于 ⌈m/2⌉ + ⌈m/2⌉ - 2 不超过上限 m-1
    3. 这个操作可能会导致父节点下溢
      1. 如果父节点是根节点并且没有元素了，那么释放它并且让合并之后的节点成为新的根节点（树的深度减小）
      2. 否则，如果父节点的元素数量小于最小值，重复上述步骤，恢复父节点的平衡

总结

上面讲了很多关于 B 树相关的知识，那 B 树到底和红黑树有什么关系呢。

我们看一下4阶B树的特点：

  1. 所有节点（包括根节点和非根节点）能存储的元素个数x ： 1<= x <=3;
  2. 所有非叶子节点的子节点个数y ： 2 <= y <=4;

下图是个红黑树

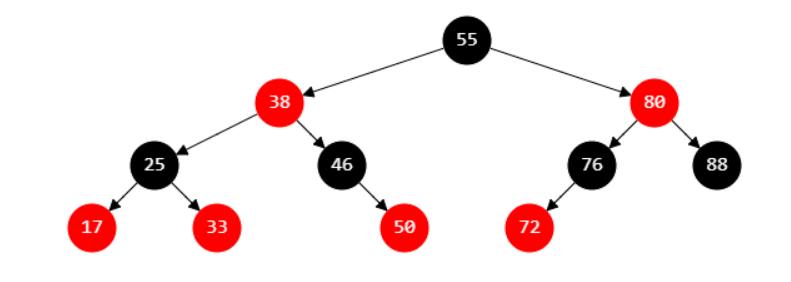
当把红色节点和它的黑色父节点放在同一个水平线上后

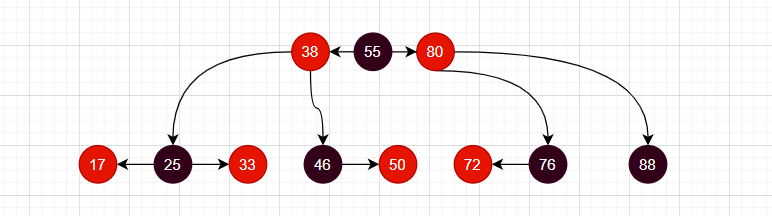
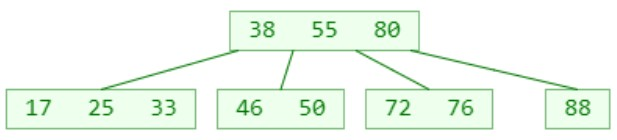
所以红黑树和4阶B树（2-3-4树）具有等价性

  • 当BLACK节点与它的RED子节点融合在一起，形成一个B树节点
  • 红黑树中BLACK的节点个数与4阶B树的节点总个数相等

看到这里，大家应该就知道B树和红黑树的关系了。对于B树我们没有进行代码说明只是逻辑的展示，下一章真正开始红黑树的时候在进行代码说明。

posted @ 2020-08-14 17:50  司霖  阅读(263)  评论(1)  编辑  收藏  举报