从零开始手撸红黑树(一)
序
学数据结构的时候,红黑树永远是逃不了的一关,同时也是相对比较难的一关.其中涉及的知识点之多,模式之复杂堪称一绝.这个系列就是从最基础的二叉树开始一步步的实现手写红黑树.
二叉树
从二叉树讲起是因为红黑树就是一种特殊的二叉树.
树的一些概念
讲二叉树免不了说一下它的一些基本概念:
首先,二叉树是一种特殊的树型数据结构,树有一些基本的概念
- 树中的元素叫做节点
- 连线相邻的节点之间的关系叫父子关系
![l3Clpq.png]()
节点
- A节点是B节点的父节点,B节点是A节点的子节点。
- C,D单个节点的父节点是同一个节点,所以他们互称为兄弟节点
- 把没有父节点的节点叫做根节点:e
- 没有子节点的节点叫做叶子节点或者叶节点
树
- 节点的高度:节点到叶子节点的最长路径(边数)
- 节点的深度:根节点到这个节点所经历的边的个数
- 节点的层数:节点的深度+1
- 树的高度:根节点的高度

高度:从下往上度量,叶子节点的高度为0
深度:从上往下度量,根节点的深度为0
层数:和深度类似,计数起点是1
二叉树的性质
前面说了,二叉树是一种特殊的树,特殊在于二叉树的一个节点的度最大为 2(最多拥有 2 颗子树)
而这个特性让二叉树有了一些性质
- 非空二叉树的第i层,最多有2^(i − 1)个节点( i ≥ 1 )
- 在高度为h的二叉树上最多有2^(h − 1)个结点(h ≥ 1)
- 对于任何一棵非空二叉树,如果叶节点个数为n0,度为2的节点个数为n2,则有n0 = n2+1
这个性质的推算如下
假设度为 1的节点个数为n1,那么二叉树的节点总数n = n0 + n1 + n2
二叉树的边数T = n1 + 2 * n2 = n – 1 = n0 + n1 + n2 -1
因此n0 = n2 + 1
特殊的二叉树们
- 真二叉树(所有非叶子节点的度都为 2)
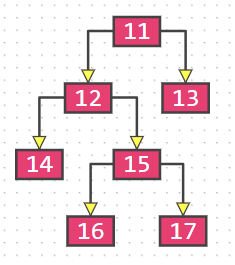
- 满二叉树(所有非叶子节点的度都为2,且所有的叶子节点都在最后一层)
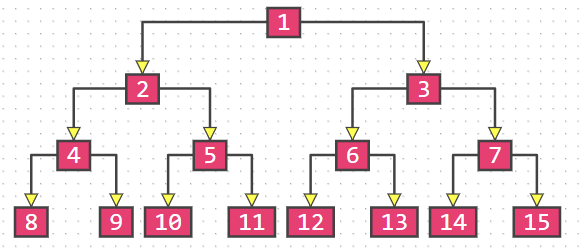
假设满二叉树的高度为h( h ≥ 1 )
那么
第i层的节点数量: 2^(i − 1)
叶子节点数量: 2^(h − 1)
总节点数量n
n = 2^h − 1 ( 2^0 + 2^1 + 2^2 + ⋯ + 2^(h−1) )
h = log2(n + 1)
- 完全二叉树(叶子节点都在最底下两层,最后一层的叶子节点都靠在左排列,并且除了最后一层,其它层的节点数都要达到最大)
![UTOOLS1586183796455.png]()
完全二叉树有以下的性质
- 度为1的节点只有左子树
- 度为1的节点要么是1个,要么是0个
- 同样节点数量的二叉树,完全二叉树的高度最小
- 假设完全二叉树的高度为h(h>=1)那么
- 至少有
2^(h-1)个节点(2^0 + 2^1 + 2^2+ ……2^(h-2) +1) - 最多有
2^h-1个节点(2^0 + 2^1 + 2^2+ ……2^(h-1))满二叉树 - 总节点数量为n,高度h=floor(log2n) +1
- 至少有
代码实现
二叉树的代码并不复杂,二叉树的代码主要是关于二叉树的遍历方式
private static class Node<E> {
E element;
Node<E> left;
Node<E> right;
Node<E> parent;
public Node(E element, Node<E> parent) {
this.element = element;
this.parent = parent;
}
}
各种遍历方式都有各自的应用场景。遍历方式详情如下
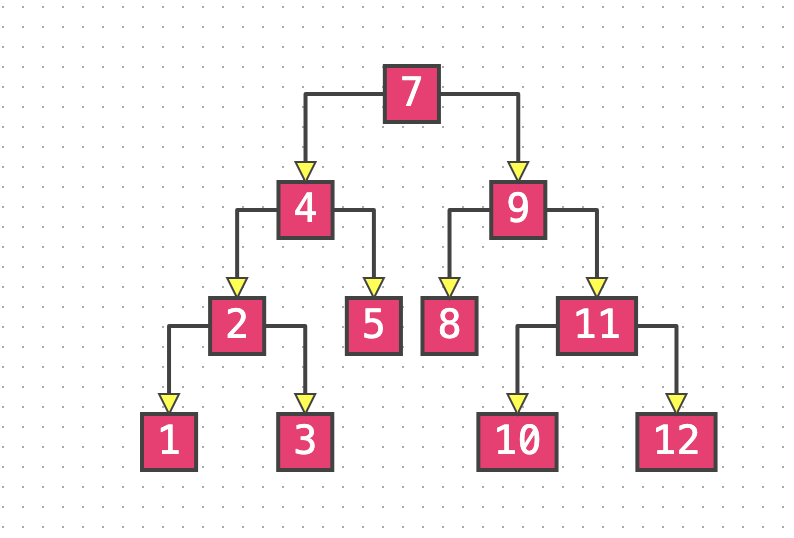
-
前序遍历
- 访问顺序: 根节点,前序遍历左子树,前序遍历右子树
private void preorder(Node<E> node) { if (node == null) { return; } System.out.println(node.element); preorder(node.left, visitor); preorder(node.right, visitor); }应用:前序遍历多用来树状的展示二叉树的结构。
上图前序遍历结果:7, 4, 2, 1, 3, 5, 9, 8, 11, 10, 12
-
中序遍历
- 中序遍历左子树,根节点,中序遍历右子树
public void inorder(Node<E> node) { if (node == null) { return; } inorder(node.left, visitor); System.out.println(node.element); inorder(node.right, visitor); }应用:二叉搜索树的中序遍历按升序或者降序处理节点
上图中序遍历结果:1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12
-
后序遍历
- 后序遍历左子树,后序遍历右子树,根节点
private void postorder(Node<E> node) { if (node == null) { return; } postorder(node.left, visitor); postorder(node.right, visitor); System.out.println(node.element); }应用:对于一些需要先子后父的操作后序遍历就派上了用场
上图后序遍历结果:1, 3, 2, 5, 4, 8, 10, 12, 11, 9, 7
-
层次遍历
- 从上到下,从左到右依次访问每个节点
- 使用队列
public void levelOrder() { if (root == null) { return; } Queue<Node<E>> queue = new LinkedList<>(); queue.offer(root); while (!queue.isEmpty()) { Node<E> node = queue.poll(); System.out.println(node.element); if (node.left != null) { queue.offer(node.left); } if (node.right != null) { queue.offer(node.right); } } }应用:
层次遍历可以在不使用递归的方式的计算出树的高度
上图在层次遍历后的结果:7, 4, 9, 2, 5, 8, 11, 1, 3, 10, 12
对于二叉树遍历的总结
前中后序遍历很好理解和记忆,都是通过递归的方式按左右子树处理顺序进行递归调用;需要记忆的是层次遍历,层次遍历使用到队列先进先出的特性将节点按层输出,可适用的场景也有很多.
关于二叉树的算法题
学数据结构后验证学习成果最佳的方式就是进行一些算法题实战
这边留几道题,感兴趣的可以实战一些:
注:前序加后序不能唯一确认一个二叉树,除非说明二叉树是真二叉树
二叉树搜索树
前面介绍了二叉树,二叉树的基础概念和二叉树的遍历方式;
这个小节就是介绍二叉树在数据结构上的一种应用;
数组是一种最基础的数据结构
对于动态数组而言,遍历搜索的平均复杂度为 O(n);
对于动态有序数组使用二分查找法,最坏时间复杂度为 O(logn),但是添加,删除的平均复杂都是 O(n);
但是二叉搜索树可以将添加,删除,搜索的最坏时间复杂度均可以优化到 O(logn)
概念介绍
二叉搜索树(Binary Search Tree)英文简称为 BST
又被称为:二叉查找树、二叉排序树
- 任意一个节点的值都大于其左子树所有节点的值
- 任意一个节点的值都小于其右子树所有节点的值
- 它的左右子树也是一棵二叉搜索树
要求:
- 存储的元素必须具有可比较性
- 比如int, double 等
- 如果是自定义类型,需要制定比较方式
- 不允许为 null
接口设计
int size() // 元素的数量
boolean isEmpty() // 是否为空
void clear() // 清空所有元素
void add(E element) // 添加元素
void remove(E element) // 删除元素
boolean contains(E element) // 是否包含某元素
二叉搜索树的节点设计
protected static class Node<E> {
E element;
Node<E> left;
Node<E> right;
Node<E> parent;
public Node(E element, Node<E> parent) {
this.element = element;
this.parent = parent;
}
public boolean isLeaf() {
return left == null && right == null;
}
public boolean hasTwoChildren() {
return left != null && right != null;
}
}
添加节点
二叉搜索树的节点添加很简单
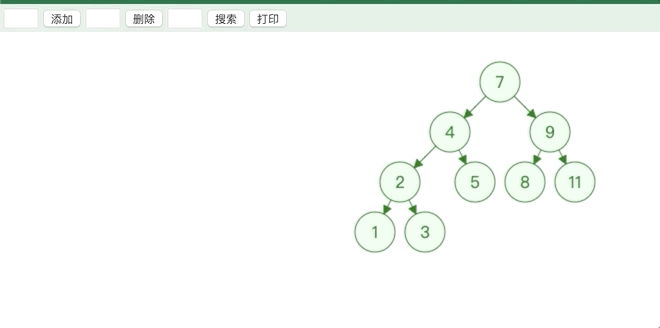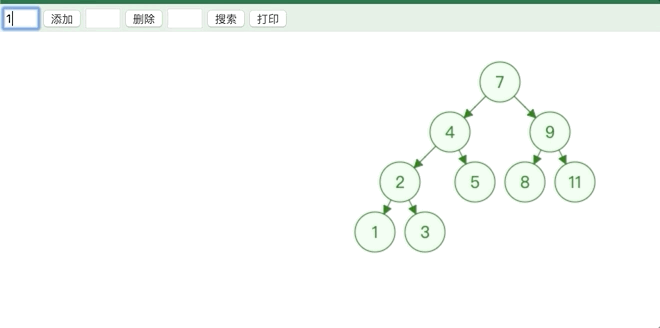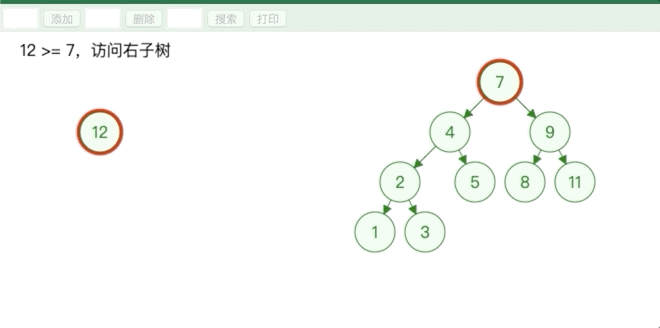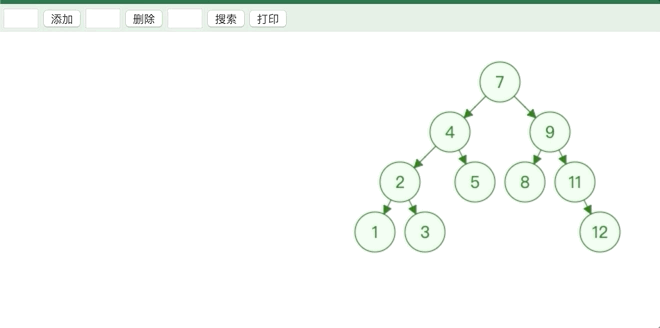
从根节点开始比较,大于所比较的节点就从其右子树继续比较,直到下个节点为空,小于所比较的节点就从其左子树继续比较.
代码实现:
public void add(E element) {
elementNotNullCheck(element);
// 添加第一个节点
if (root == null) {
root = new Node<>(element, null);
size++;
return;
}
// 添加的不是第一个节点
// 找到父节点
Node<E> parent = root;
Node<E> node = root;
int cmp = 0;
while (node != null) {
cmp = compare(element, node.element);
parent = node;
if (cmp > 0) {
node = node.right;
} else if (cmp < 0) {
node = node.left;
} else { // 相等
return;
}
}
// 看看插入到父节点的哪个位置
Node<E> newNode = new Node<>(element, parent);
if (cmp > 0) {
parent.right = newNode;
} else {
parent.left = newNode;
}
size++;
}
删除节点
删除二叉搜索树分 3 种情况讨论
- 被删除的节点是叶子节点的时候
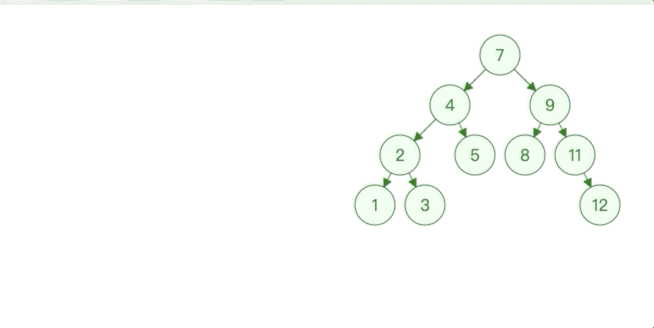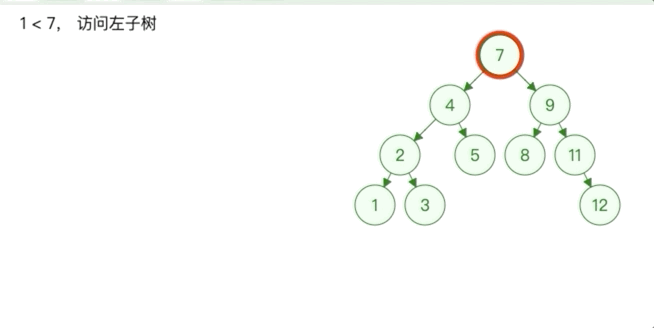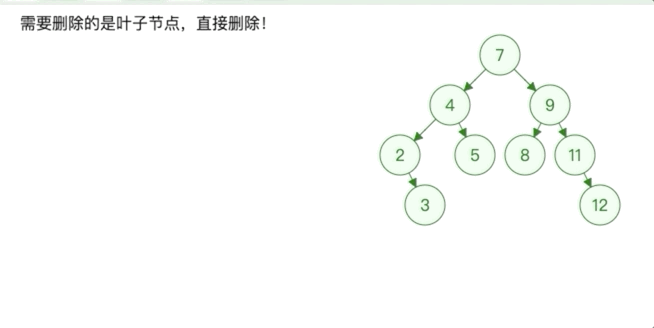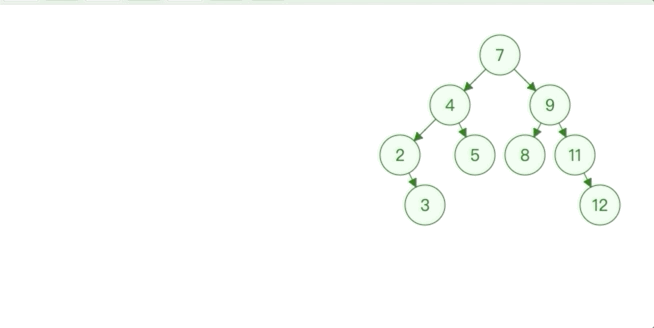
直接删除,根据该节点是其父节点的左节点还是右节点修改二叉树,如果该节点是根节点则树为空
if (node == node.parent.left) {
node.parent.left = null
}
if (node == node.parent.right) {
node.parent.right = null
}
if (node.parent == null) {
root = null
}
- 删除的节点度为 1
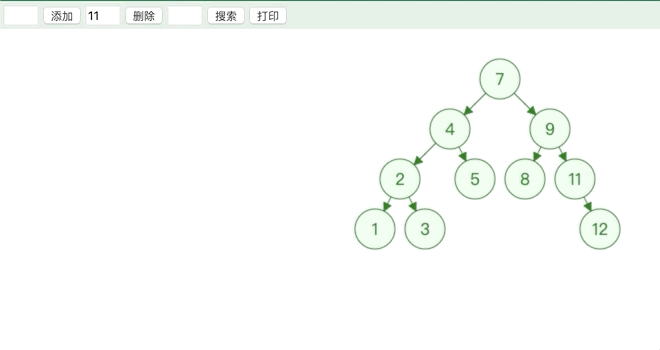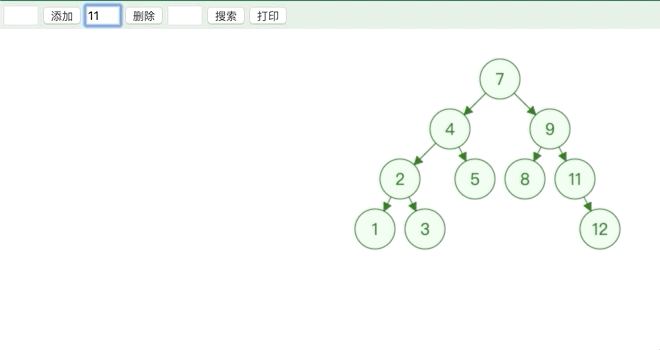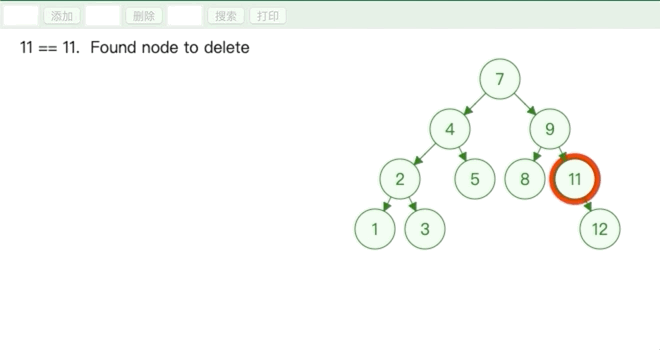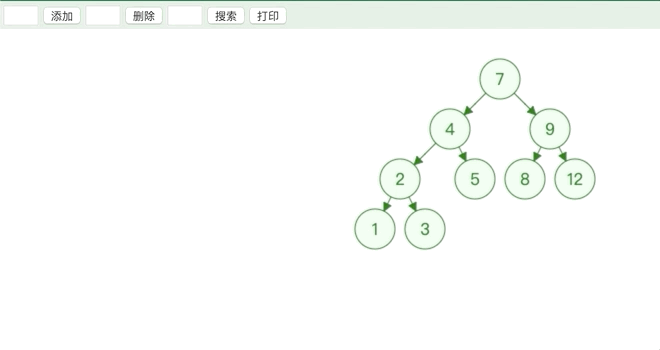
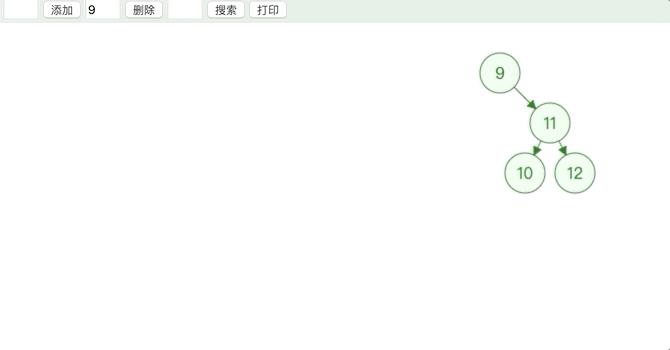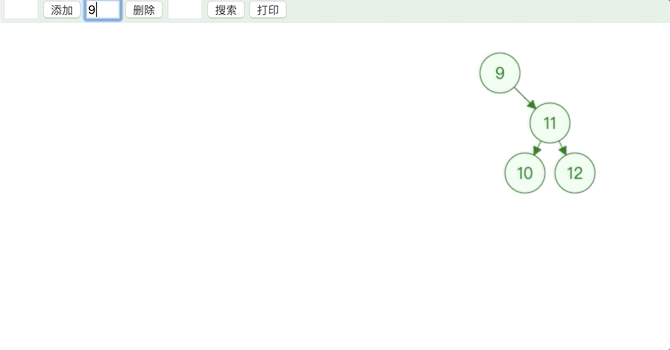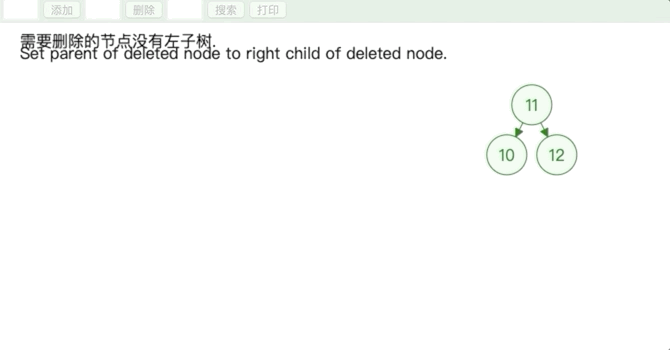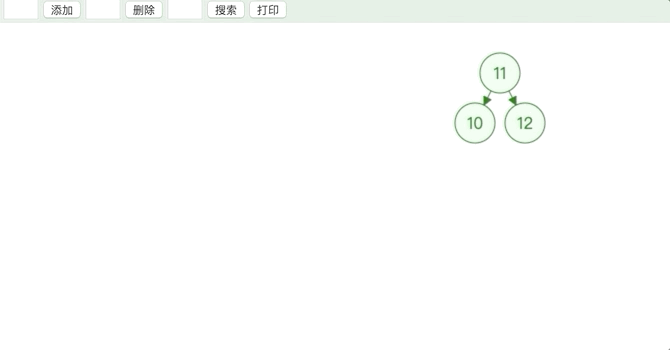
用子节点替代原节点的位置
如果 node 是左子节点
child.parent = node.parent
node.parent.left = child
如果 node 是右子节点
child.parent = node.parent
node.parent.right = child
如果 node 是根节点
root = child
- 删除度为 2 的节点
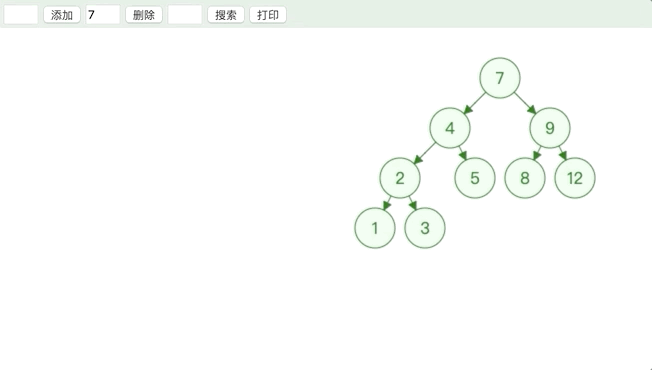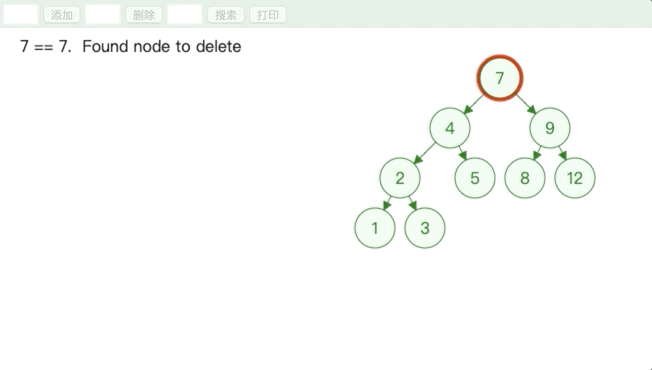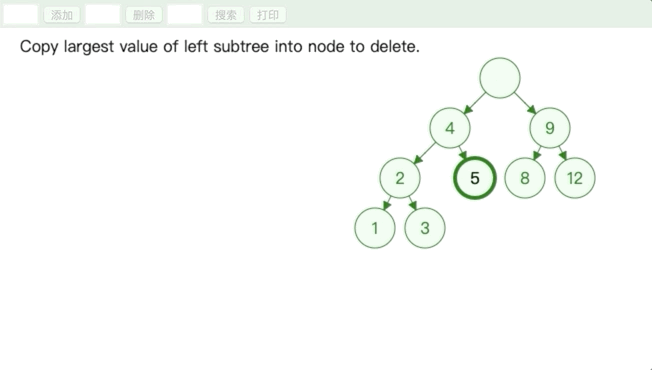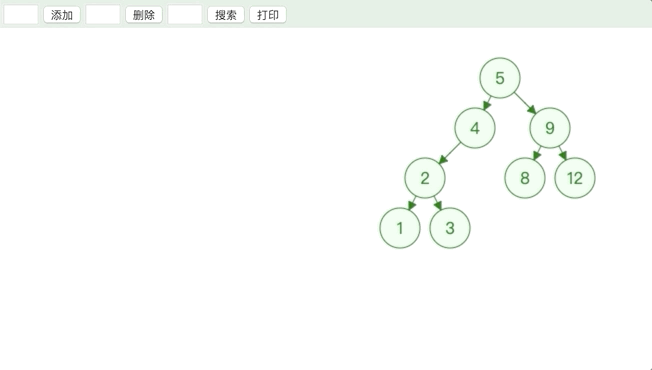
删除叶子节点和度为 1 的节点都很好理解,删除度为 2 的节点有点儿绕,用上图举例,删除 7 这个节点的时候,如果直接删除会使得左右子树分离,所以只能替换值,保留节点之间的连接.
为了保持二叉搜索树的性质,用来替换的值必须比 7 这个节点的左节点大,比右节点小.所以使用 7 这个节点的前驱节点或者后继节点来替代 7 这个节点.
操作:
先用前驱或者后继节点的值覆盖原节点的值
然后删除响应的前驱节点或者后继节点,前驱或后继节点肯定为叶子节点,删除方式和删除叶子节点的方式一致
前驱节点:中序遍历时的前一个节点,在二叉搜索树中前驱节点就是比它小的第一个节点
后继节点:中序遍历时的后一个节点,在二叉搜索树中后继节点就是比它大的第一个节点
这边举一个后继节点的代码实现为例
protected Node<E> successor(Node<E> node) {
if (node == null) return null;
// 后继节点在右子树当中(right.left.left.left....)
Node<E> p = node.right;
if (p != null) {
while (p.left != null) {
p = p.left;
}
return p;
}
// 从父节点、祖父节点中寻找后继节点
while (node.parent != null && node == node.parent.right) {
node = node.parent;
}
return node.parent;
}
以上就是删除一个二叉搜索树中节点的分析
下面就是实际的代码实现
private void remove(Node<E> node) {
if (node == null) return;
size--;
if (node.hasTwoChildren()) { // 度为2的节点
// 找到后继节点
Node<E> s = successor(node);
// 用后继节点的值覆盖度为2的节点的值
node.element = s.element;
// 删除后继节点
node = s;
}
// 删除node节点(node的度必然是1或者0)
Node<E> replacement = node.left != null ? node.left : node.right;
if (replacement != null) { // node是度为1的节点
// 更改parent
replacement.parent = node.parent;
// 更改parent的left、right的指向
if (node.parent == null) { // node是度为1的节点并且是根节点
root = replacement;
} else if (node == node.parent.left) {
node.parent.left = replacement;
} else { // node == node.parent.right
node.parent.right = replacement;
}
} else if (node.parent == null) { // node是叶子节点并且是根节点
root = null;
} else { // node是叶子节点,但不是根节点
if (node == node.parent.left) {
node.parent.left = null;
} else { // node == node.parent.right
node.parent.right = null;
}
}
}
二叉搜索树总结
以上我们探讨了二叉搜索树的添加和删除,二叉搜索树的查找并不复杂就不一一实现了,看官们可以自己实现试试.
二叉搜索树确实可以使得我们的搜索,添加,删除等操作的时间复杂度变成 O(logn).但是也有缺点,如果按顺序添加节点是二叉搜索树会退化为链表,时间复杂度就不在是 O(logn)了,这个时候就需要用到我们的平衡二叉树了,经典常见的平衡二叉搜索树有AVL 树和红黑树(点题了),下节我就带大家手撸一个 AVL 树和红黑树.
最后留几个二叉搜索树相关的算法题供大家实战




 浙公网安备 33010602011771号
浙公网安备 33010602011771号