算法学习：二叉树

二叉树

概念

树中的元素叫做节点
连线相邻的节点之间的关系叫父子关系

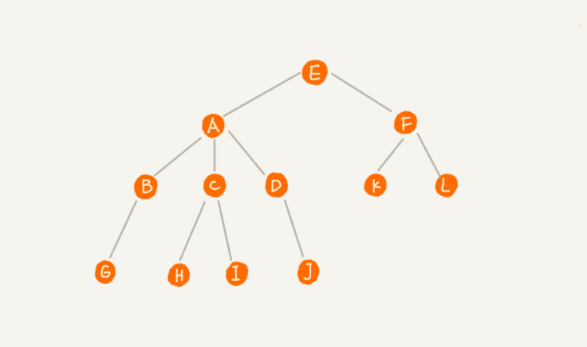
节点

1. A节点是B节点的父节点，B节点是A节点的子节点。
2. C，D单个节点的父节点是同一个节点，所以他们互称为兄弟节点
3. 把没有父节点的节点叫做根节点
4. 没有子节点的节点叫做叶子节点或者叶节点

树

1. 节点的高度：节点到叶子节点的最长路径（边数）
2. 节点的深度：根节点到这个节点所经历的边的个数
3. 节点的层数：节点的深度+1
4. 树的高度：根节点的高度

高度：从下往上度量，叶子节点的高度为0
深度：从上往下度量，根节点的深度为0
层数：和深度类似，计数起点是1

二叉树

编号为2的二叉树，叶子结点都在最底层，除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树叫做满二叉树

标号3的二叉树中，叶子节点都在最底下两层，最后一层的叶子节点都靠在左排列，并且除了最后一层，其它层的节点数都要达到最大，这种二叉树叫做完全二叉树。

存储

• 链式存储法
  每个节点有三个字段，一个存储数据，另外两个指向左右子节点的指针。
  

• 顺序存储法
  基于数组的顺序存储法，根节点存储在下标i=1的位置，那左节点存储在下标2*i = 2的位置，右子节点存储在2*i = 1 = 3的位置，以此类推
  
  如果二叉树是个完全二叉树，那用数组存储是最节省内存的一种方式

二叉树的遍历

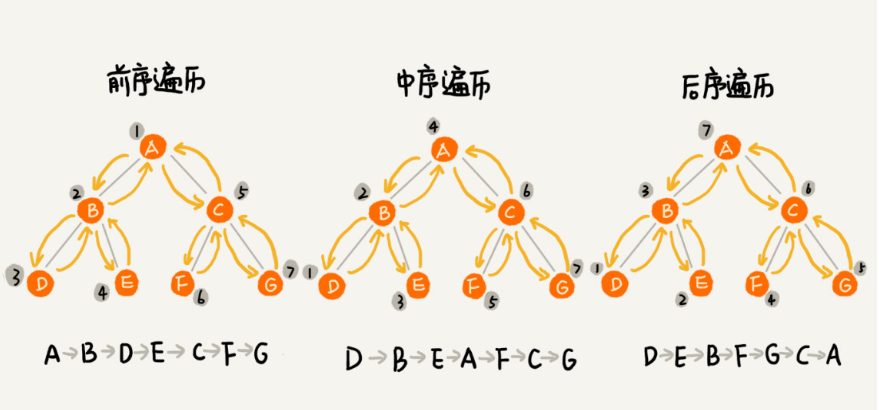
遍历分为三种方式：前序遍历，中序遍历和后序遍历
前，中，后表示节点在它的左右子树节点遍历打印的先后顺序。

• 前序遍历是指，对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树
• 中序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树
• 后序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。
  

前中后序遍历是一种递归的过程。
前序遍历，其实就是先打印根节点，然后再递归地 打印左子树，左后递归打印右子树
递推公式的关键就是，如果要解决问题A，就假设子问题B，C已经解决，然后再看如何利用B，C解决A,

//前序遍历的递推公式：
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right);

//中序遍历的递推公式：
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right);

//后序遍历的递推公式：
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r;

void preOrder(Node* root) {
  if (root == null) return;
  print root // 此处为伪代码，表示打印 root 节点
  preOrder(root->left);
  preOrder(root->right);
}

void inOrder(Node* root) {
  if (root == null) return;
  inOrder(root->left);
  print root // 此处为伪代码，表示打印 root 节点
  inOrder(root->right);
}

void postOrder(Node* root) {
  if (root == null) return;
  postOrder(root->left);
  postOrder(root->right);
  print root // 此处为伪代码，表示打印 root 节点
}

二叉树遍历的时间复杂度：
每个节点最多被访问两次，时间复杂度和节点的个数n成正比，为O（n）