[2018南京预赛]Lpl and Energy-saving Lamps

一、题面

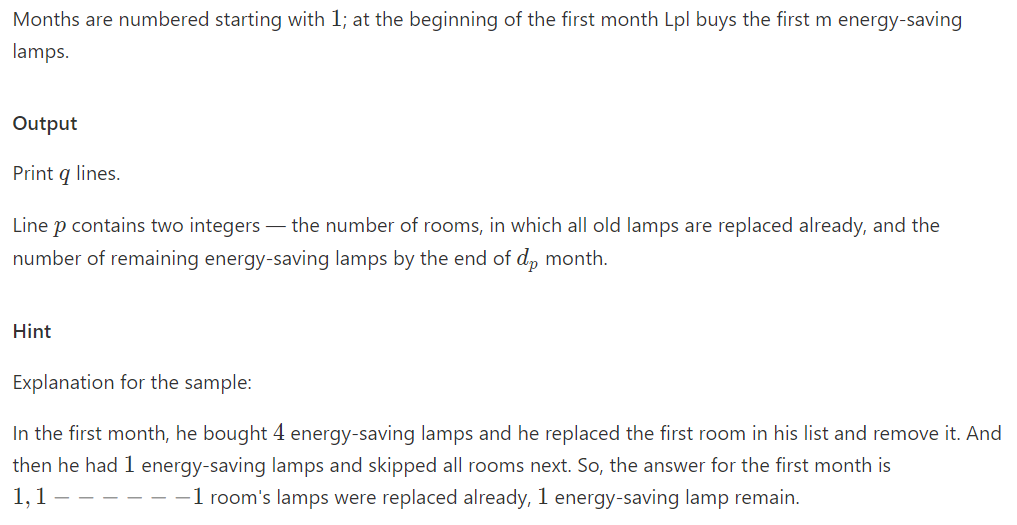
样例输入：

5 4
3 10 5 2 7
10
5 1 4 8 7 2 3 6 4 7

样例输出：

4 0
1 1
3 6
5 1
5 1
2 0
3 2
4 4
3 6
5 1

 

二、思路

关键词：线段树

这道题最难就难在看题吧。。。也许ACM的魅力之一便在于此——面对若干道题，你不知每一道题的难度是高是低，只能耐心地读清题面，审清题意，理清思路，方可知其是否在能力范围内以及预估耗时。考试过程中，我基本靠board来判断题目难度，清北大佬们先AC了哪些我就先做哪些。。。然而这道题似乎他们也不太愿意读题？其实际难度我觉得可能还要低于其他几道更早被A的题目。

题目大意是：现每个月提供m个灯泡，每次选出第一个小于当前灯泡数的房间，更换好该房间的灯泡，直至不存在这样的房间，则进入下个月。给出若干次月份数，求这几个月内能更换多少个房间的灯泡，以及剩余灯泡数。注意：当所有房间更换完之后，将不再提供灯泡！

n <= 10 ^ 5, d[p] <= 10 ^ 5，暴搜不可行。题目核心无非是求最早出现的小于k的数，可以用线段树维护每一段的最小值，再进行单点修改。水的一批。

 

三、代码

#include <cstdio>
#define MAXN 100005
#define INF 0x3f3f3f3f

int n, m, T, a[MAXN], x, t[MAXN << 2], k, l[MAXN], r[MAXN], q, mx, tot;

int max(int a, int b) {
    return a > b ? a : b;
}

int min(int a, int b) {
    return a < b ? a : b;
}

void build(int o, int l, int r) {
    if (l == r) {
        scanf("%d", &x), t[o] = x;
        return;
    }
    int m = (l + r) >> 1;
    build(o << 1, l, m), build(o << 1 | 1, m + 1, r);
    t[o] = min(t[o << 1], t[o << 1 | 1]);
}

int query(int o, int l, int r) {
    if (l == r) return l;
    int m = (l + r) >> 1;
    if (t[o] > k) return 0;
    return t[o << 1] <= k ? query(o << 1, l, m) : query(o << 1 | 1, m + 1, r);
}

void upd(int o, int l, int r) {
    if (l == r) {
        k -= t[o], t[o] = INF;
        return;
    }
    int m = (l + r) >> 1;
    if (q <= m) upd(o << 1, l, m);
    else upd(o << 1 | 1, m + 1, r);
    t[o] = min(t[o << 1], t[o << 1 | 1]);
}

void work() {
    for (int i = 1; i <= mx; i++) {
        if (tot != n) {
            k += m;
            while (q = query(1, 1, n)) upd(1, 1, n), tot++;
        }
        l[i] = k, r[i] = tot;
    }
}

int main() {
    scanf("%d %d", &n, &m);
    build(1, 1, n);
    scanf("%d", &T);
    for (int i = 1; i <= T; i++) scanf("%d", &a[i]), mx = max(a[i], mx);
    work();
    for (int i = 1; i <= T; i++) printf("%d %d\n", r[a[i]], l[a[i]]);
    return 0;
}