[知识点]网络流基础

零、目录

　　I、网络流基础

　　II、网络流进阶之转换对偶图

　　III、网络流进阶之费用流

 

一、前言

这是ACM之路的第一篇文章，是在通过看自己OI生涯的文章来回顾知识点的过程中，实在难以接受当时过于含糊笼统的介绍的情况下决定开写的，真是对不住1300+的阅读量了。由于网络流的EK算法和Dinic算法就是早期的知识点系列文章，当时确实疏漏很多，现在通过我目前残缺的知识框架和基本功重新整理一下。

网络流是一个很广泛的问题，是一种类比水流的解决方案。从算法角度来看，最常见的基础算法为Dinic算法，也是本文最重要的部分。从问题角度而言，对于算法竞赛，最常见的问题莫过于最大流问题。何为最大流问题，我们先通过一道例题的题面来体会。

我们以图片的形式来简化题干要求。

 

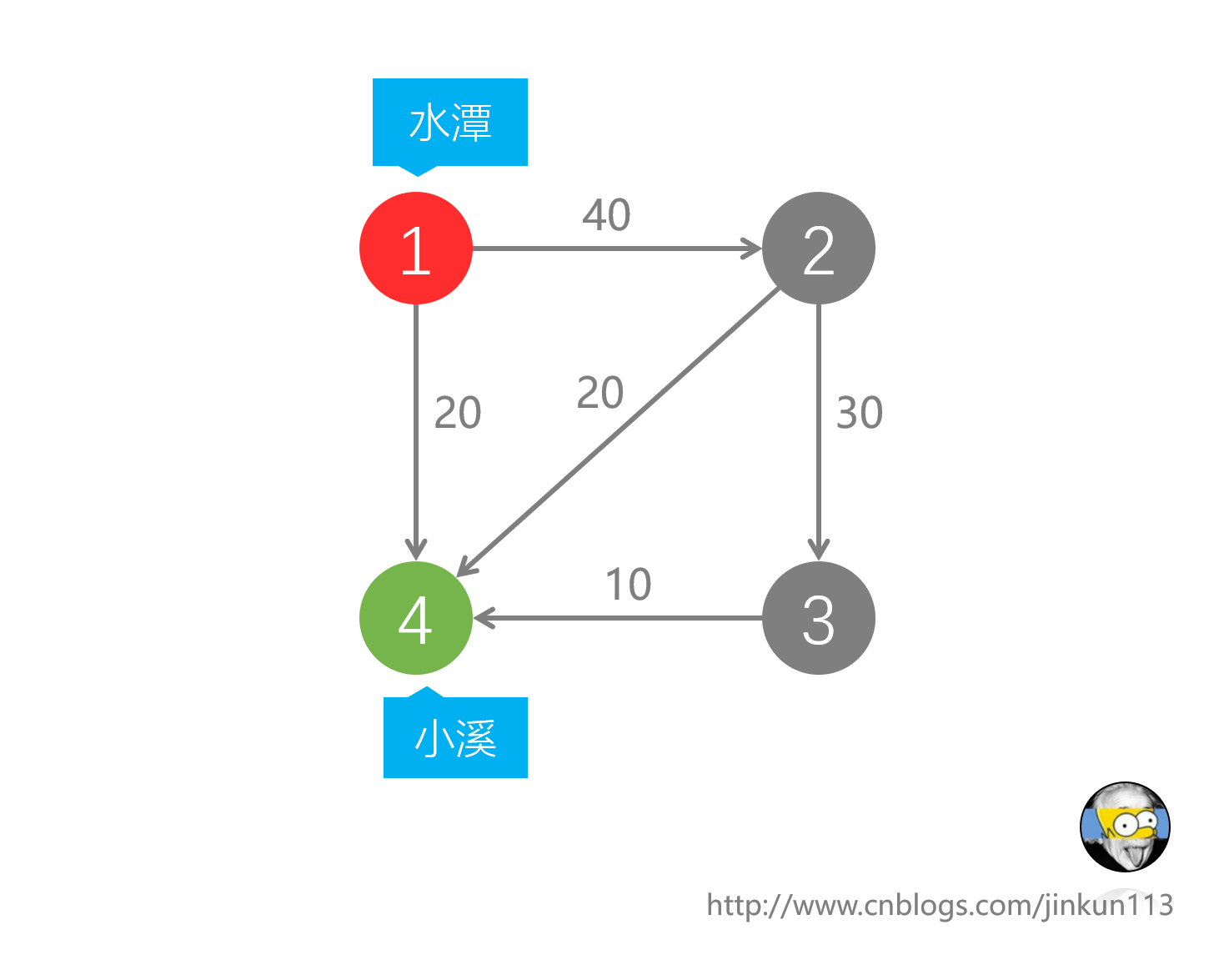
设图中存在4个节点，其中1号为水潭，即水流的源点，4号为小溪，即水流的汇点，2、3号为其余的交叉点。节点之间存在带权排水沟，其权值表示水流在这条沟中的最大流量。任务就是从1号节点至4号节点最多能有多大的水流量。

先轻松地人脑分析一下——由图可知，从1号至4号可流20；从1号至2号虽然可流40，但2号的所有可流出的沟中总流量只有30；其中直接至4号的流量为20；至3号的流量为10，原因是3号至4号也只可流10。综上，总流量为20+30=50。

 

二、最大流问题

上述题便是总经典的最大流问题的模板题。不难有一种思路——每次对图进行搜索，寻找一条从源点通向汇点的路，并记录这条路上的最小流量，将每一条支路均减去该流量即可。如果你已经懂了，恭喜你你已经轻而易举地掌握了所谓的Edmon-Karp算法。天哪网络流简直不要太好理解？？？那我们再来看一张图：

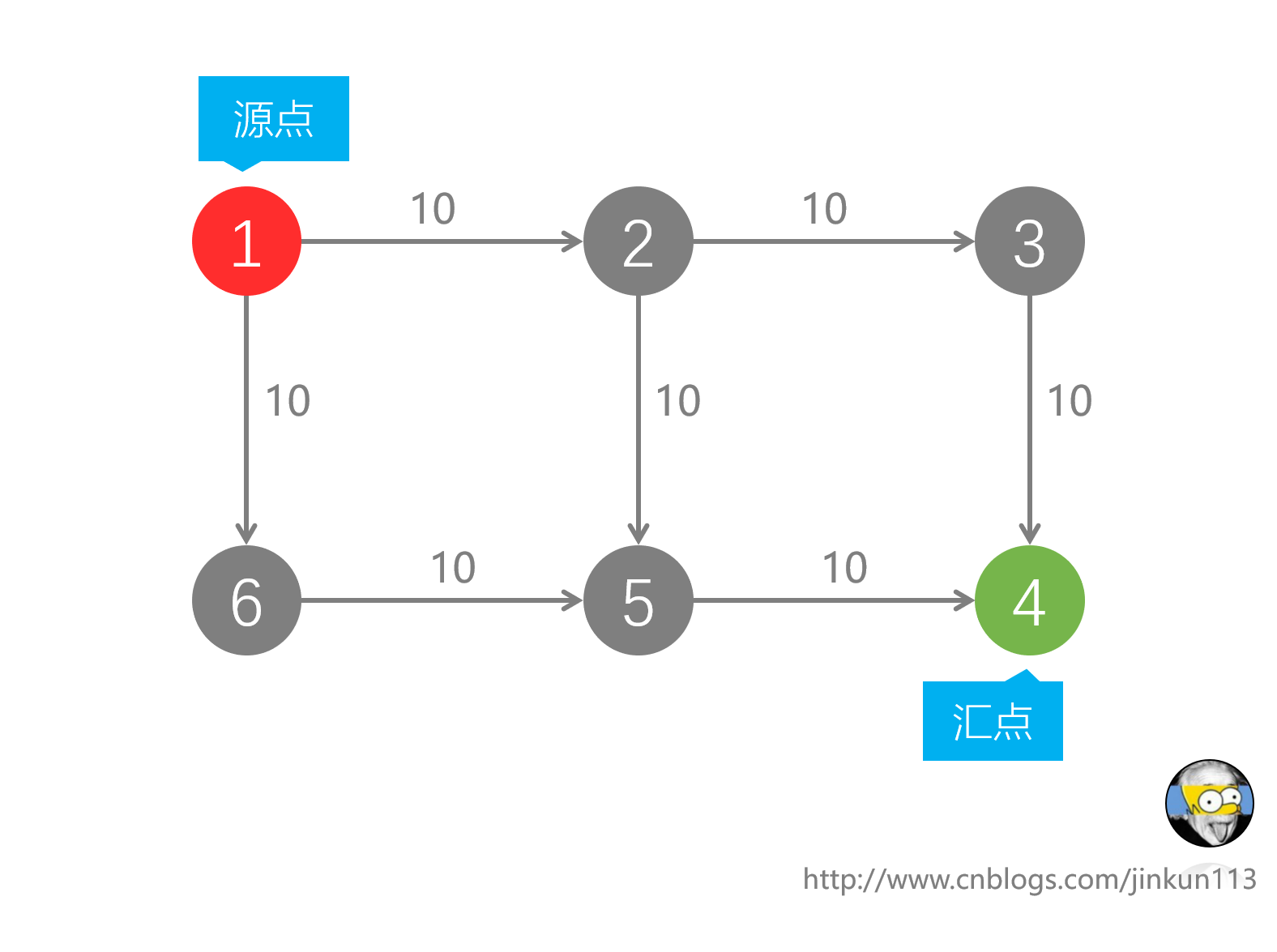
来来来告诉我最大流为多少？

第一条路：1-2-3-4，流量为10；第二条路：1-6-5-4，流量为10。总流量20。完美。

但我们假设一种情况——如果计算机先选择了1-2-5-6这条路？从原理上来看，显然没有毛病；但是一旦1-2-5-6被选择，这就意味着——接下来并没有流量可以流了，而结果也就停留在了10，显然与答案不符。

什么鬼？？？

也就是说，之前的策略显然不是最优的，而我们已不能操纵程序改变已选择的路——自己走的路跪着都要走完。时至如今，有什么反悔药可以吃嘛？有啊。

我们先给每条路开个后门——设置一条流量为0的反向的路，称作反向弧。

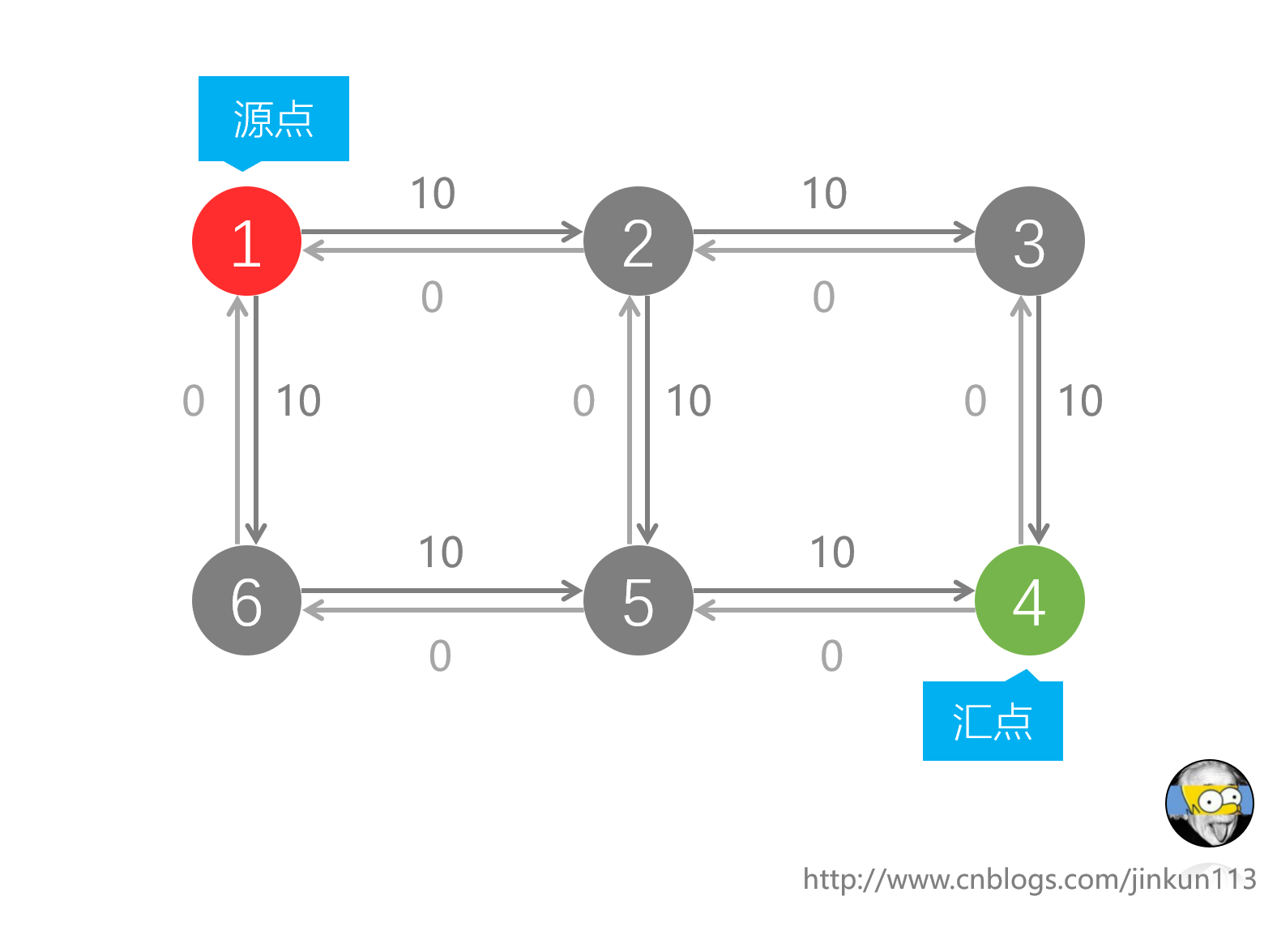
如上，我们现在选择了1-2-5-6，在给1-2,2-5,5-6三条路流量清零的同时，给2-1,5-2,6-5这三条反向弧增加10流量。在没有反向弧的时候可以发现并没有路可走了，但现在我们可以另辟蹊径选择1-6-5-2-3-4：

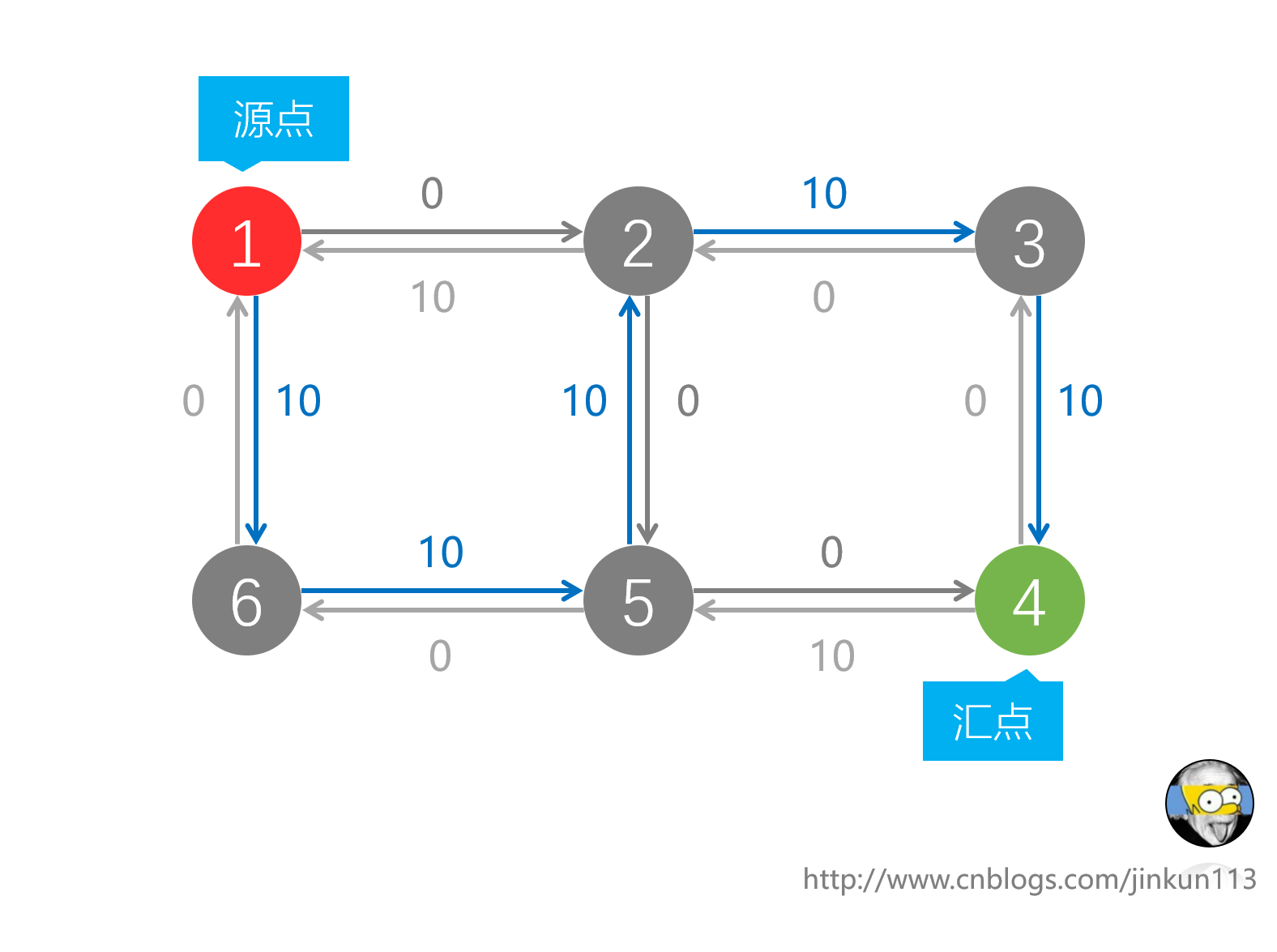
这样，最大流求得20，即答案。

反向弧的作用是：在当前存在更好选择的时候会使之前选择的弧会被撤销。反向弧之所以有流量，是因为刚刚选择了该反向弧的正向弧，而下一次选择的时候如果经过该反向弧，则该弧正反向抵消，起到反悔作用。

 

三、Dinic算法

前面所述的Edmon-Karp算法好理解——但如此一遍遍的全图跑DFS，时间复杂度可想而知。在正确性落实后，我们考虑进行一定优化提高效率。是时候搬出Dinic算法了。

Dinic算法的核心在于：

1、对图进行BFS，绘制出层次图，即对每一个节点进行标记，记录其与源点的距离，称为dep深度。如第一张图所示，dep[] = {0, 0, 2, 2, 1}；

2、对图进行DFS，过程基本同EK算法，但在搜索过程中，只遍历至当前节点深度+1的节点。

3、反复进行1、2操作，直至第1步层次图中汇点dep值为空，即没有路可抵达汇点，表示最大流已求出，即完成任务。

 

四、例题与代码

题干见上。

Dinic算法代码：

#include <cstdio>
#include <cstring>

#define MAXN 205
#define MAXM 205
#define INF 0x3f3f3f3f

int m, n, u, v, f, q[MAXN * MAXN], h[MAXN], d[MAXN], o = 1, ans;

struct Edge {
    int v, next, f;
} e[MAXM << 1];

int min(int a, int b) {
    return a < b ? a : b;
}

void add(int u, int v, int f) {
    o++, e[o] = (Edge) {v, h[u], f}, h[u] = o;
}

bool BFS() {
    int head = 1, tail = 2;
    q[1] = 1, d[1] = 1;
    while (head != tail) {
        int o = q[head];
        for (int x = h[o]; x; x = e[x].next) {
            int v = e[x].v;
            if (!d[v] && e[x].f > 0) d[v] = d[o] + 1, q[tail++] = v;
        }
        head++;
    }
    return d[n] != 0;
}

int DFS(int o, int mif) {
    int res = 0;
    if (mif <= 0 || o == n) return mif;
    for (int x = h[o]; x; x = e[x].next) {
        int v = e[x].v;
        if (d[v] == d[o] + 1) {
            int of = DFS(v, min(mif, e[x].f));
            e[x].f -= of, e[x ^ 1].f += of, mif -= of, res += of;
            if (!mif) break;
        }
    }
    return res;
}

int main() {
    scanf("%d %d", &m, &n);
    for (int i = 1; i <= m; i++) scanf("%d %d %d", &u, &v, &f), add(u, v, f), add(v, u, 0);
    while (BFS()) ans += DFS(1, INF), memset(d, 0, sizeof(d)); 
    printf("%d", ans);
    return 0;
}

 

五、后记

后续将跟进费用流等更深入的问题。