[Codeforces] Round #320 (Div.2)

1、前言

虽然这次我依旧没有参加正式比赛，但是事后还是看了看题目的。。。一般不怎么刷Codeforces。

 

A、Raising Bacteria

You are a lover of bacteria. You want to raise some bacteria in a box.

Initially, the box is empty. Each morning, you can put any number of bacteria into the box. And each night, every bacterium in the box will split into two bacteria. You hope to see exactly x bacteria in the box at some moment.

What is the minimum number of bacteria you need to put into the box across those days?

 

>Input

The only line containing one integer x (1 ≤ x ≤ 109).

 

>Output

The only line containing one integer: the answer.

 

>Sample test(s)

 

input

5

output

2

 

input

8

output

1

 

>Note

For the first sample, we can add one bacterium in the box in the first day morning and at the third morning there will be 4 bacteria in the box. Now we put one more resulting 5 in the box. We added 2 bacteria in the process so the answer is 2.

For the second sample, we can put one in the first morning and in the 4-th morning there will be 8 in the box. So the answer is 1.

 

题解：找出所给数中包含多少个2^k（k∈[1,30]）即可。

-------------------------------------------------------------------------------------------

#include<cstdio>

int n,tot;

int main()
{
　　scanf("%d",&n);
　　for (int i=1<<30;i>=1;i>>=1) if (n>=i) n-=i,tot++;
　　printf("%d",tot);
　　return 0;
}

-------------------------------------------------------------------------------------------

 

B、Finding Team Member

There is a programing contest named SnakeUp, 2n people want to compete for it. In order to attend this contest, people need to form teams of exactly two people. You are given the strength of each possible combination of two people. All the values of the strengths aredistinct.

Every contestant hopes that he can find a teammate so that their team’s strength is as high as possible. That is, a contestant will form a team with highest strength possible by choosing a teammate from ones who are willing to be a teammate with him/her. More formally, two people A and B may form a team if each of them is the best possible teammate (among the contestants that remain unpaired) for the other one.

Can you determine who will be each person’s teammate?

 

>Input

There are 2n lines in the input.

The first line contains an integer n (1 ≤ n ≤ 400) — the number of teams to be formed.

The i-th line (i > 1) contains i - 1 numbers ai1, ai2, ... , ai(i - 1). Here aij (1 ≤ aij ≤ 106, all aij are distinct) denotes the strength of a team consisting of person i and person j (people are numbered starting from 1.)

 

>Output

Output a line containing 2n numbers. The i-th number should represent the number of teammate of i-th person.

>Sample test(s)

input

2
6
1 2
3 4 5

output

2 1 4 3

input

3
487060
3831 161856
845957 794650 976977
83847 50566 691206 498447
698377 156232 59015 382455 626960

output

6 5 4 3 2 1

>Note

In the first sample, contestant 1 and 2 will be teammates and so do contestant 3 and 4, so the teammate of contestant 1, 2, 3, 4 will be2, 1, 4, 3 respectively.

 

题解：求得所有对的默契值，从大到小排序，然后一一配对，如果已经配对过则跳过。

-------------------------------------------------------------------------------------------

#include<cstdio>
#include<algorithm>
#define MAXN 320005
using namespace std;

struct Num
{
　　int val,x,y;
};
Num a[MAXN];

struct Cmp
{
　　bool operator () (Num a,Num b)
　　{
　　　　return (a.val>b.val);
　　}
};
Cmp x;

int n,tot,ans[810];

int main()
{
　　scanf("%d",&n);
　　for (int i=2;i<=2*n;i++)
　　for (int j=1;j<=i-1;j++) scanf("%d",&a[++tot].val),a[tot].x=i,a[tot].y=j;
　　sort(a+1,a+tot+1,x);
　　for (int i=1;i<=tot;i++)
　　{
　　　　if (ans[a[i].x] || ans[a[i].y]) continue;
　　　　ans[a[i].x]=a[i].y,ans[a[i].y]=a[i].x;
　　}
　　for (int i=1;i<=2*n;i++) printf("%d ",ans[i]);
　　return 0;
}

-------------------------------------------------------------------------------------------

C. A Problem about Polyline

 

There is a polyline going through points (0, 0) – (x, x) – (2x, 0) – (3x, x) – (4x, 0) – ... - (2kx, 0) – (2kx + x, x) – ....

We know that the polyline passes through the point (a, b). Find minimum positive value x such that it is true or determine that there is no such x.

 

>Input

Only one line containing two positive integers a and b (1 ≤ a, b ≤ 109).

 

>Output

Output the only line containing the answer. Your answer will be considered correct if its relative or absolute error doesn't exceed 10 - 9. If there is no such x then output  - 1 as the answer.

 

>Sample test(s)

input

3 1

output

1.000000000000

input

1 3

output

-1

input

4 1

output

1.250000000000

>Note

You can see following graphs for sample 1 and sample 3.

 

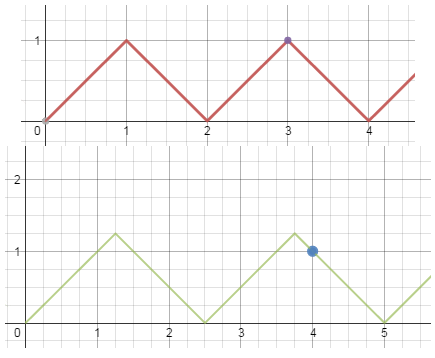
题解：首先可以确定的是，该函数由y=x延伸而来。因为点在直线上，显然b<a无解；否则分为两种情况，一种是点(a,b)在斜率为1的线上，那么这个线段过（a-b,0）这个点，同理如果在斜率为-1的线上，那么这个线段过(a+b,0)这个点。

-------------------------------------------------------------------------------------------

#include <cstdio>

int a,b;

int main()
{
　　scanf("%d %d",&a,&b);
　　if (a<b) printf("-1");
　　else printf("%.12f\n",(a+b)/(2.0*((a+b)/(2*b))));
　　return 0;
}

-------------------------------------------------------------------------------------------