[知识点]Tarjan算法

// 此博文为迁移而来，写于2015年4月14日，不代表本人现在的观点与看法。原始地址：http://blog.sina.com.cn/s/blog_6022c4720102vxnx.html

 

UPDATE - 20210604：调整格式，重新制图，修正各种错误，更清晰地描述 Tarjan 算法的过程（三年一更（照道理应该重新写一篇，但太懒辣

UPDATE（20180809）：对代码和描述进行大量修改。

UPDATE（20151104）：新增Tarjan算法核心代码。

 

1、前言

我始终记得去年冬天有天吃完饭后，我们在买东西的时候讨论着强连通分量和 Tarjan 什么的。当时我真的什么都没听懂啊。。。什么强连通图，强连通分量，极大强连通分量。。。当然现在还是知道了。

2、概念

Tarjan 算法，由 Tarjan 发明。作用在于求图中的强连通分量。什么是强连通？在有向图 G 中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。如果有向图 G 的每两个顶点都强连通，称 G 是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。

先举一个很简单的例子，下图中，子图 {1, 2, 3, 4} 中的结点两两可达，所以子图 {1, 2, 3, 4} 为一个强连通分量。

 

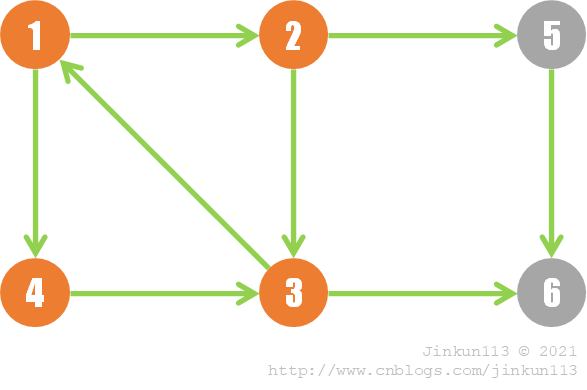
求强连通分量除了枚举，还有两种 O(N + M) 的方法 —— Kosaraju 算法或 Tarjan 算法，其中 Tarjan 算法较为常用。

 

3、求强连通分量

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。

首先定义两个数组：

① dfn[i]，表示结点 i 的搜索次序编号，即搜索到结点 i 时的时间戳；

② low[i]，表示结点 i 至多经过一条非树边（即不包含于以结点 i 为根的子树的边）能够到达且当前在栈中的所有结点的 dfn 值（时间戳）的最小值。

（通过学弟提及和 dd 的友好交流，我们了解到，目前关于 Tarjan 算法的 low 数组的定义分为两种：一种为上述表达，一种为“表示结点 i 及其子树能够追溯到且当前在栈中的所有结点的 dfn 值（时间戳）的最小值”，即不考虑经过几条边。前者为标准表述，而后者在求强连通分量时同样是保证正确性的，但网上诸多博客将两者混为一谈，包括本博文之前的版本亦是，采用第二种定义形式的同时又以第一种定义形式来写具体步骤与代码，易误导新人（以及我）。所以，这里我们从头到尾均以第一种正确表述来介绍 Tarjan 算法的思想）

于是存在一个定理（也是最核心的判断方法）：当 dfn[i] = low[i] 时，以 i 为根的搜索子树上所有的结点表示一个强连通分量。

上述定义相当拗口，下面为以上图为例的具体操作步骤，更易理解：

(1) 从起点 1 开始搜索，直到没有出边，先后遍历结点 1, 2, 5, 6，根据时间先后顺序，它们的 dfn 值分别为 1, 2, 3, 4，同时因为每次搜索到当前结点时尚不存在以其自身为根的子树，故 low 值就等于 dfn 值，如图所示。此时栈内为 {1, 2, 5, 6}，由于结点 6 没有出边，即不存在子树，则其 dfn[6] = low[6] = 4 的值不会再发生改变，则 {6} 为一个强连通分量；

(2) 回溯至结点 5，此时栈内为 {1, 2, 5}，同样有 dfn[5] = low[5] = 3，且结点 5 没有出边，同理得 {5} 是一个强连通分量；

 

(3) 回溯至结点 2，存在出边，继续搜索到结点 3，此时栈内为 {1, 2, 3}，发现结点 3 存在一条子边连向已经在栈中的结点 1，如紫色边所示，则可得 low[3] = dfn[1] = 1。另一条边连向结点 6，但是 6 没有在栈中；

(4) 回溯至结点 2，更新 low[2]，即 low[2] = low[3] = 1；

(5) 回溯到结点 1，存在出边，继续搜索到结点 4，存在一条边与在栈中的 3 相连，边 (4, 3) 为非树边，则 low[4] = dfn[3] = 5。至此，所有结点遍历结束。

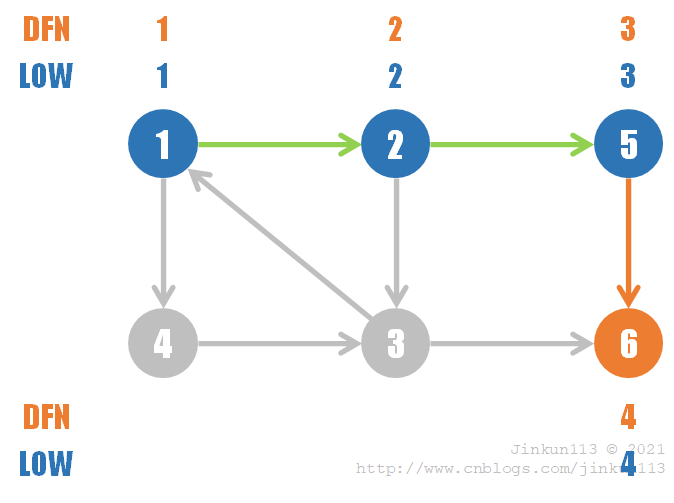
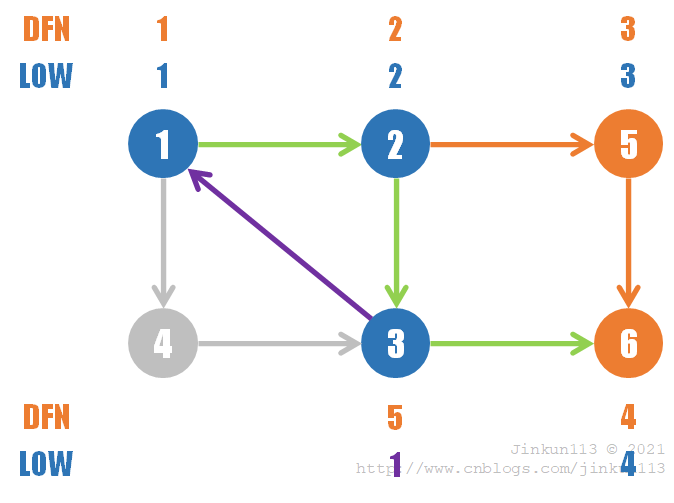
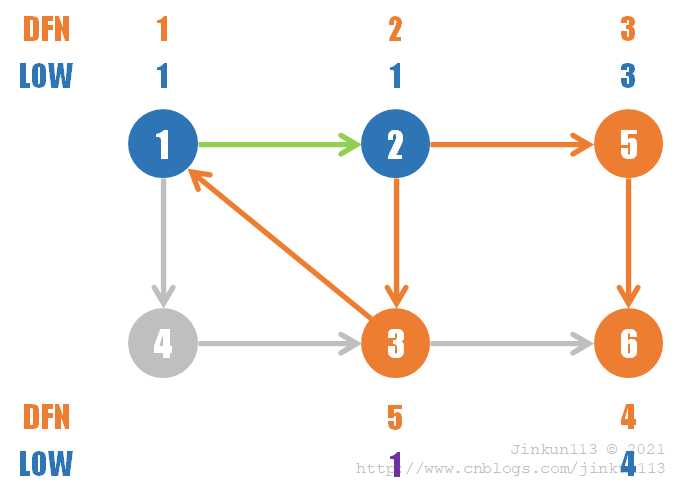
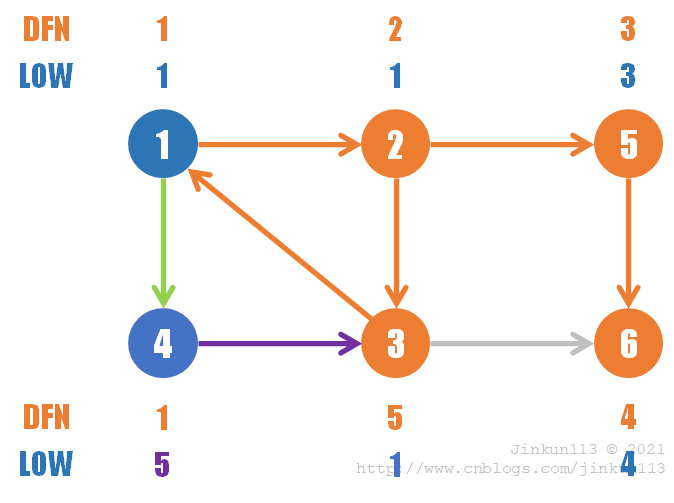
(6) 回溯到结点 1，dfn[1] = low[1] = 1 仍不变，则在栈中的 {1, 2, 3, 4} 组成了一个强连通分量。算法结束。

综上所述，求得的三个强连通分量为：{1, 2, 3, 4}，{5}，{6}。

代码：

#include <bits/stdc++.h>
using namespace std;

#define MAXN 1005
#define MAXM 10005

int o, n, m, u, v;
int h[MAXN], ins[MAXN], dfn[MAXN], low[MAXN];
int tim, st[MAXN << 1], t, tot, top[MAXN];
int ans[MAXN][MAXN];

struct Edge {
    int v, next;
} e[MAXM];

void add(int u, int v) {
    o++, e[o] = (Edge) {v, h[u]}, h[u] = o;
}

void tarjan(int o) {
    dfn[o] = low[o] = ++tim, ins[o] = 1, st[++t] = o;
    for (int x = h[o]; x; x = e[x].next) {
        int v = e[x].v;
        if (!dfn[v]) 
            tarjan(v), low[o] = min(low[o], low[v]);
        else 
            if (ins[v]) low[o] = min(low[o], dfn[v]);
    }
    if (dfn[o] == low[o]) {
        int x; 
        tot++;
        do {
            x = st[t--];
            ins[x] = 0;
            ans[tot][++top[tot]] = x;
        } while (x != o);
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) 
        cin >> u >> v, add(u, v);
    for (int i = 1; i <= n; i++) 
        if (!dfn[i]) tarjan(i);
    for (int i = 1; i <= tot; i++) {
        for (int j = 1; j <= top[i]; j++) 
            cout << ans[i][j] << ' ';
        cout << endl;
    }
    return 0;
}

（之前提及的仅适用于求强连通分量的第二种定义，只需要将代码中 L27 的 low[o] = min(low[o], dfn[v]) 修改为 low[o] = min(low[o], low[v]) 即可）

 

4、缩点

其实上面，Tarjan算法本身已经讲完，但是，强连通分量求了肯定不是用来玩的。后面会给出一道许运用到Tarjan+缩点的题目，现在先讲概念。缩点的意思很简单，将一个强连通分量缩成一个点。作用不言而喻：如果题目所给的图存在环，还可以走重复的路，同时又要你求出权值和最大，怎么办？将强连通分量缩成点，接下来的任务就很简单了。在进行Tarjan求强连通分量的时候，我们就可以提前处理好一些内容，如得出缩点后的节点数，以及每个节点所属的强连通分量

缩点的过程有两种方式，根据情况可以选择：

① 双图法

缩点后的节点全部重新存在新的图中。该方法的空间需求较大，但是一点都不麻烦。

② 新节点法

如果原图存在n个节点，求出了k个非一个节点的强连通分量，则新加k个节点，共(n+k)个节点。在处理第i个强连通分量的时候，将所有与i中节点相连的边连到新的节点(n+i)，同时对强连通分量中的节点全部进行标记（对边标记也可以），下次搜索的时候不可进行访问。

 

5、例题

抢掠计划 [APIO 2009]

S城中的道路都是单向的。不同的道路由路口连接。按照法律的规定， 在每个路口都设立了一个 S 银行的 ATM 取款缩机。令人奇怪的是，S 的酒吧也都设在路口，虽然并不是每个路口都设有酒吧。 B 计划实施 S 有史以来最惊天动地的 ATM 抢劫。他将从市中心 出发，沿着单向道路行驶，抢劫所有他途径的 ATM 机，最终他将在一个酒吧庆祝他的胜利。 使用高超的黑客技术，他获知了每个 ATM 机中可以掠取的现金数额。他希 望你帮助他计计算从市中心出发最后到达某个酒吧时最多能抢劫的现金总数。他可 以经过同一路口或道路任意多次。但只要他抢劫过某个 ATM 机后，该 ATM 机 里面就不会再有钱了。 例如，假设该城中有 6 个路口，道路的连接情况去网上找吧。

 

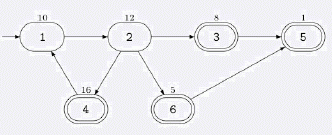
市中心在路口 1，由一个入口符号→来标识，那些有酒吧的路口用双圈来表示。每个 ATM 机中可取的钱数标在了路口的上方。在这个例子中，B 能抢劫的现金总数为 47，实施的抢劫路线是：1-2-4-1-2-3-5。

输入格式

第一行包含两个整数 n、m。n 表示路口的个数，m 表示道路条数。接下来 m 行，每行两个整数，这两个整数都在 1 到 n 之间，第 i+1 行的两个整数表示第 i 条道路的起点和终点的路口编号。接下来 n 行，每行一个整数，按顺序表示每 个路口处的 ATM 机中的钱数。接下来一行包含两个整数 s、p，s 表示市中心的 编号，也就是出发的路口。p表示酒吧数目。接下来的一行中有 p 个整数，表示 p 个有酒吧的路口的编号。

输出格式

输出一个整数，表示 B 从市中心开始到某个酒吧结束所能抢劫的最多的现金总数。

数据范围

50%的输入保证 n, m<=3000。所有的输入保证n, m<=500000。每个 ATM 机中可取的钱数为一个非负整数且不超过 4000。输入数据保证你可以从市中心沿着 s 的单向的道路到达其中的至少一个酒吧。

输入样例

6 7
1 2
2 3
3 5
2 4
4 1
2 6
6 5
10 12 8 16 1 5
1 4
4 3 5 6

输出样例

47

主要到图中没有边权而有点权，且要求点权综合越大越好。就样例而言，出现的环对结果没有影响，但搜索的时候很难处理，延伸到所有强连通分量其实均可看为一点，故可使用Tarjan算法求出所有强连通分量，并进行缩点。这里采用的是上述的双图法，直接将所求的的所有强连通分量放进一个新图中。转化时注意一些细节即可。

但由于本题数据较大，n/m <= 500000，爆栈感觉是件轻而易举的事情。这里仅提供较朴素的Tarjan+搜索算法，得分率为80%，存在TLE * 1和RE * 2。

#include <cstdio>

#define MAXN 500005
#define MAXM 500005

int n, m, u[MAXN], v[MAXN], tw[MAXN], ts, p, to, tb[MAXN], th[MAXN];
int w[MAXN], b[MAXN], s, h[MAXN], o, lik[MAXN];
int dfn[MAXN], low[MAXN], ins[MAXN], st[MAXN], tot, t, tim;
int f[MAXN], ans;

struct Edge {
    int v, next;
} e[MAXM], te[MAXM];

int min(int a, int b) {
    return a < b ? a : b; 
}

int max(int a, int b) {
    return a > b ? a : b; 
}

void add(int u, int v, int t) {
    if (t) to++, te[to] = (Edge) {v, th[u]}, th[u] = to;
    else o++, e[o] = (Edge) {v, h[u]}, h[u] = o;
}

void init() {
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= m; i++) scanf("%d %d", &u[i], &v[i]), add(u[i], v[i], 1);
    for (int i = 1; i <= n; i++) scanf("%d", &tw[i]);
    scanf("%d %d", &ts, &p);
    for (int i = 1; i <= p; i++) scanf("%d", &o), tb[o] = 1;
}

void tarjan(int o) {
    dfn[o] = low[o] = ++tim, ins[o] = 1, st[++t] = o;
    for (int x = th[o]; x; x = te[x].next) {
        int v = te[x].v;
        if (!dfn[v]) tarjan(v), low[o] = min(low[v], low[o]);
        else if (ins[v] && dfn[v] < low[o]) low[o] = dfn[v];
    }
    if (dfn[o] == low[o]) {
        int x; tot++;
        do x = st[t--], ins[x] = 0, lik[x] = tot; while (x != o); 
    }
}

void rebuild() {
    for (int i = 1; i <= m; i++) if (lik[u[i]] != lik[v[i]]) add(lik[u[i]], lik[v[i]], 0);
    for (int i = 1; i <= n; i++) {
        w[lik[i]] += tw[i]; 
        if (i == ts) s = lik[i];
        if (tb[i]) b[lik[i]] = 1;
    }
    f[s] = w[s];
}

void DFS(int o) {
    if (b[o]) ans = max(ans, f[o]);
    for (int x = h[o]; x; x = e[x].next) {
        int v = e[x].v;
        if (f[o] + w[v] > f[v]) f[v] = f[o] + w[v], DFS(v);
    }
}

int main() {
    init();
    for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i);
    rebuild();
    DFS(s); 
    printf("%d", ans);
    return 0;
}

 

参考：

https://zhuanlan.zhihu.com/p/161537289