[知识点] 8.2 图的存储与遍历
总目录 > 8 图论 > 8.2 图的存储与遍历
前言
写到这里,不免想起当年高一的 NOIP2014 因为把邻接链表给写错了而差 5 分错过一等奖导致一路再起不能。
子目录列表
1、概述
2、边存储
3、邻接矩阵
4、邻接表
5、图的遍历
8.2 图的存储与遍历
1、概述
数据结构往往有两种存储方式 —— 顺序和链式。顺序采用数组,链式多采用链表,图虽然结构复杂,但其实也是以这两种思路对其进行存储,只不过更为麻烦。
首先,图的读入方式基本上是给定图的点数 n 和边数 m,然后对于 m 条边,每条边给定 u 和 v。
下面以有向赋权图举例(无向图直接视作双向边即可)
2、边存储
① 概念
直接将给定的 m 组 (u, v) 用数组存下来。
② 示例
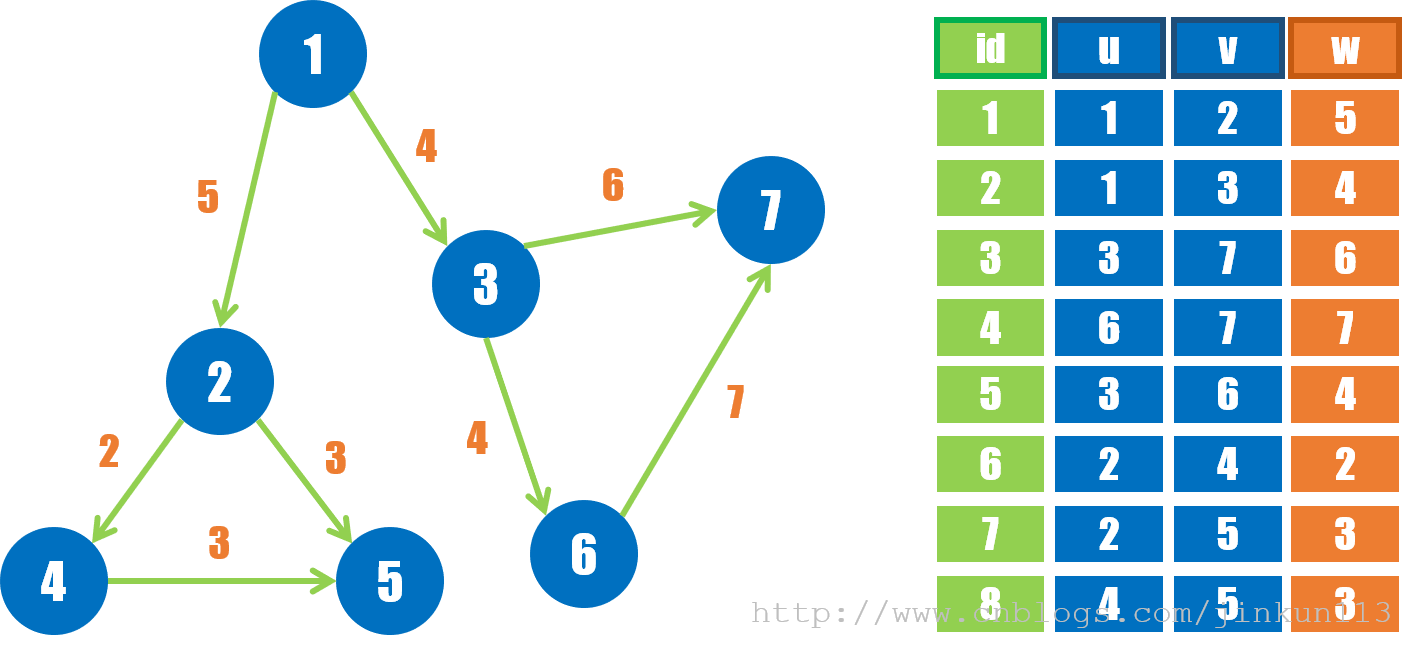
③ 优劣势
优势:
在最小生成树(请参见:8.3 最小生成树)中的 Kruskal 算法中,因为需要将边按边权排序,需要直接存边。
劣势:
遍历效率极低,时间复杂度高达 O(n * m),除特别需求基本不会采用。
④ 代码
void add(int o, int _u, int _v, int _w) { u[o] = _u, v[o] = _v, w[o] = _w; }
3、邻接矩阵
① 概念
使用一个二维数组 a 来存储边,其中 a[u][v] = 1(无权图)/ 权值(赋权图) 时表示 u 和 v 之间存在一条边,= 0 时则不存在。根据权值范围,也可以用 -1 或其他方式表示不存在边。属于顺序存储结构。
② 示例

③ 优劣势
优势:
构建简单,能 O(1) 查询两点之间是否存在边。
劣势:
空间复杂度过高 —— O(n ^ 2),尤其在稀疏图中浪费了大量空间,n 在 5000+ 时空间就高达 128MB 的上限了。同时,邻接矩阵无法判断重边,遍历效率 O(n ^ 2) 同样不理想。
④ 代码
void add(int u, int v, int w) { a[u][v] = w; }
4、邻接表
① 概念
使用 n 个可动态调整元素的数据结构构成的数组来存边,其中第 u 个数组的第 i 个元素表示以点 u 为起点的第 i 个终点。如果是赋权图,则需要使用结构体或类来同时存储终点与边权,必要的话可以存更多信息。属于链式存储结构。
对于 C++,可以使用 STL 中的 vector;普适性更强的则是使用邻接链表(链式前向星),即使用 n 个链表来存储。
② 示例
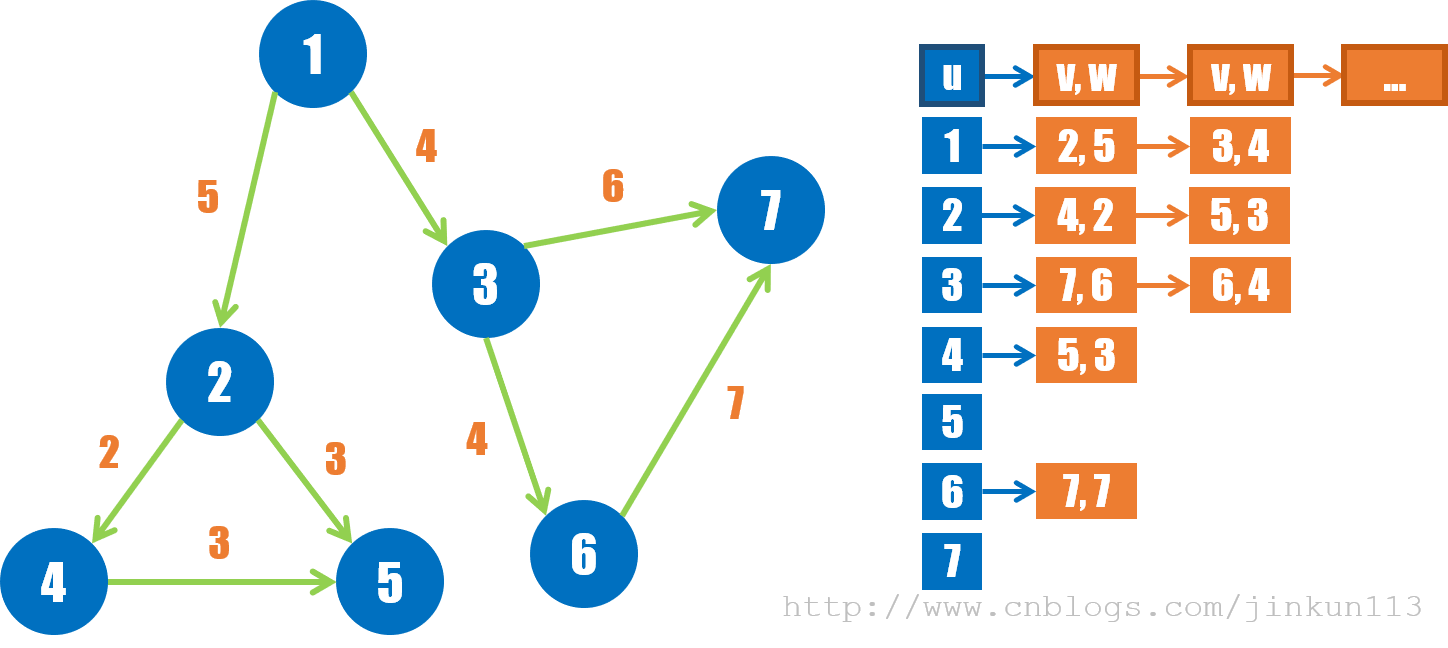
③ 构建步骤
以使用链表为例。首先,对每个读入的边赋予一个编号 [1, m],以便于链表的建立与访问。建立一个类 Edge,存储每条边的终点 v,边的权值 w,以及预留的链表中后继边的指针 nxt(不需要使用指针变量,但本质上是指针)。建立一个 h 数组,其中 h[i] 表示以结点 i 为起点的边的链表头编号,初始为 0。每读入一条边 (u, v),则更新第 u 条链表,将边存入 Edge 并链到给链表的链表头,其后继边的编号即原本链表头的边的编号 h[u],再更新链表头编号 h[u] 为当前的 Edge。
觉得麻烦的可以使用 vector,效率会较低,但更易理解。
④ 优劣势
优势:
基本能应用到所有场合,遍历时间复杂度 O(n + m),空间复杂度 O(m) 都是无与伦比的。
劣势:
构建与遍历等操作使用起来会比邻接矩阵麻烦,不能 O(1) 查询边的存在。
其他:
如果需要对以某个点为起点的所有出边进行某种排序,则只能使用 vector。
⑤ 代码(使用链表)
1 class Edge { 2 public: 3 int v, w, nxt; 4 } e[MAXM]; 5 6 void add(int u, int v, int w) { 7 tot++, e[tot] = (Edge) {v, w, h[u]}, h[u] = tot; 8 }
5、图的遍历
在第三章的 3.1 DFS / BFS 搜索 中,我们已经介绍了 DFS / BFS,广义上它们用于进行各种搜索,而狭义本属于树与图的一种遍历算法,这里再以图的视角回顾一次。
DFS,深度优先搜索,指在对树或图的遍历中,优先访问深度更深的结点。对于树而言,其实就是先序遍历,这里不提;对于图而言,DFS 相当于每次访问到一个新的结点后,马上访问其第一个后继结点,直到没有后继再回溯,再访问下一个后继结点,每次访问打上访问标记。
BFS,深度优先搜索,指在对树或图的遍历中,优先访问当前深度的结点。对于树而言,其实就是层次遍历,这里不提;对于图而言,DFS 相当于每次访问到一个新的结点后,会将其后继结点全部访问一次,再逐一访问其后继结点,每次访问打上访问标记。
以上面的图为例,体现 DFS 与 BFS 的访问顺序的不同(假设从结点 1 开始访问):
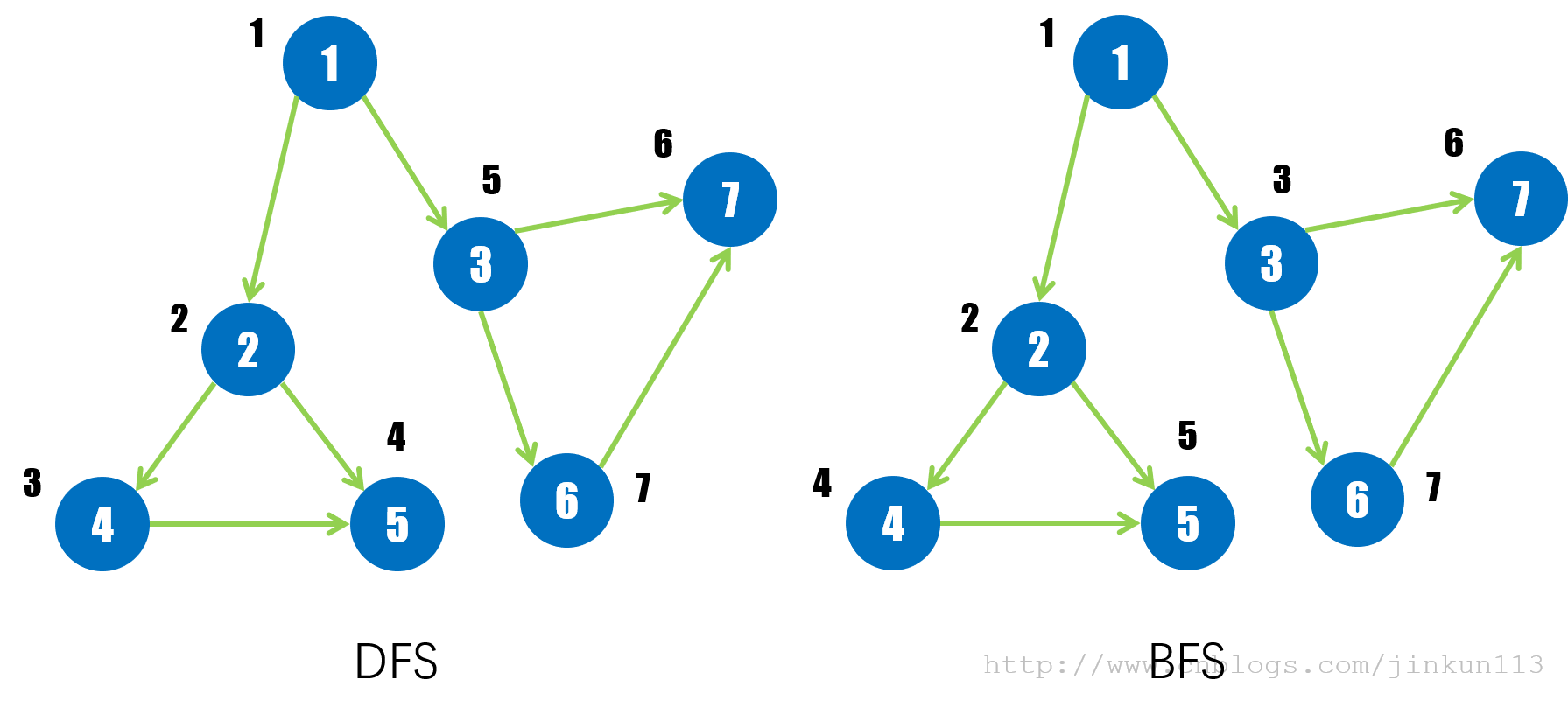
以邻接链表为图的存储方式,两种算法时间复杂度均为 O(n + m),空间复杂度均为 O(n)。
当然,遍历只是一个框架,实际运用中,是在遍历的过程中求得图上的各种信息以输出或进行后续操作,比如求最短路径,连通块,最小环等等。
下面给出 DFS 与 BFS 最基础的遍历代码:
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 #define MAXN 1005 5 #define MAXM 10005 6 7 int h[MAXN], tot, n, m, u, v, w, vis[MAXN]; 8 9 class Edge { 10 public: 11 int v, w, nxt; 12 } e[MAXM]; 13 14 void add(int u, int v, int w) { 15 tot++, e[tot] = (Edge) {v, w, h[u]}, h[u] = tot; 16 } 17 18 void dfs(int o) { 19 for (int x = h[o]; x; x = e[o].nxt) { 20 int v = e[x].v; 21 if (!vis[v]) vis[v] = 1, dfs(v); 22 } 23 } 24 25 void bfs() { 26 int head = 1, tail = 2, q[MAXN]; 27 q[1] = vis[1] = 1; 28 while (head != tail) { 29 int o = q[head]; 30 for (int x = h[o]; x; x = e[o].nxt) { 31 int v = e[x].v; 32 if (!vis[v]) { 33 vis[v] = 1; 34 q[tail] = v, tail++; 35 } 36 } 37 head++; 38 } 39 } 40 41 int main() { 42 cin >> n >> m; 43 for (int i = 1; i <= m; i++) { 44 cin >> u >> v >> w; 45 add(u, v, w), add(v, u, w); 46 } 47 vis[1] = 1, dfs(1); 48 memset(vis, 0, sizeof(vis)); 49 bfs(); 50 return 0; 51 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号