[知识点] 7.3 树与二叉树
总目录 > 7 数据结构 > 7.3 树与二叉树
前言
不知道为啥原网站竟然没有对树——数据结构最为重要的基本结构(没有之一)——有单独的介绍板块,我觉得必不可少!后面众多高级数据结构都是以树为结构的,所以这一部分很必要。
(后来才发现树被归纳到了图论章节,虽然树和图确实紧密相连,但我觉得还是归类到数据结构部分更好)
子目录列表
1、形象的树
2、二叉树的概念
3、二叉树的存储
4、二叉树的遍历
5、树的存储和遍历
6、哈夫曼树
7、树与图
7.3 树与二叉树
1、形象的树
如果你说生活中你不知道栈是什么,队列是什么,链是什么,树就不可能不知道了 —— 各式各样的树遍布大街小巷,它或如柳树般翩翩淑女,或如槐树般魁梧高大,但它们的结构却有鲜明的共同特点:扎根于地,向上生长,生出分枝,分枝再生出更小的分枝。
而作为数据结构的一种,树和客观世界中的树极其相似:
① 不同于栈,队列,数组等线性表,树是一种非线性结构,是由 n(n >= 0) 个结点组成的有限集;
② n >= 1 时,结点中有且仅有一个结点被称为根结点;
③ n >= 2 时,除去根结点,其余 n - 1 个结点是 m 个互不相交的结点有限集,又可以看做 m 棵树,并且都被称作根的子树;
④ 对于这 m 棵子树,它们都有自己的根结点,即与整棵树的根结点直接相连的那个结点。对于任意一棵子树,除去其根结点,其余结点又是若干个互不相交的结点有限集,以此递归;
⑤ 如果结点除去与其直接相连的所属子树的根结点而没有其他相连结点,则这个结点称为叶子结点。
上述就是对抽象数据类型树的定义。
正如其名,确实很抽象,拿出一棵树来展示一下:

和客观世界中的树的表象差别在于:数据结构的树一般把根放在最上方而向下伸展。
从上述过程不难看出,树的构建和遍历过程是需要通过递归(请参见:2.2 递归与分治)完成的 —— 从根结点递归到叶子结点,再回溯。
而结合家族族谱来看树结构,对其许多相关术语就能轻松理解,还是上图:
假设这是张三家的族谱,张三的编号为 9,那么根结点 1 是他的曾祖父,2 是他的祖父,4 是他的父亲,对于其他结点,也是这样的关系,所以:
① 对于 4 而言,9 是它的儿子结点,反之,4 是 9 的父亲结点;
② 对于 10 而言,11 是它的兄弟结点,4 和 5 同理;
③ 对于 9 而言,10, 11 是它的堂兄弟结点,12 和 13 同理;
④ 对于 1 而言,2 ~ 13 所有结点都是它的子孙结点,反之,1 是 2 ~ 13 的祖先结点。
除此之外,还有:
① 度:结点拥有的子树个数称为结点的度;各结点的度的最大值称为树的度;
比如,9 的度为 0,5 的度为 2,3 的度为 3,这棵树的度为 3。
② 层次:根结点的层次定义为第一层,其儿子结点为第二层,以此类推。也就是说,同层次的所有非兄弟结点可互称为堂兄弟;
③ 深度:所有结点层次的最大值为树的深度;
比如,这棵树的深度为 4。
还有一些概念:
① 有序树和无序树:有序树中的子结点存在次序,比如对于 1 而言,2 是它的第一个儿子节点,3 是第二个;无序树则不存在。
② 森林:m 棵互不相交的树的集合。对于非叶子结点而言,其子树的集合即是一片森林。
2、二叉树的概念
① 概念
二叉树是一种特殊的树形结构,它的每个结点至多只有 2 棵子树,即不存在度 > 2 的结点。放在家族族谱里,可以理解为这个家族所在的国家实行 Family Planning 政策,至多只能生 2 个儿子。
二叉树属于有序树,即对于任意一个非叶子结点,其子树有左右之分,其儿子结点分为左儿子结点和右儿子结点,如下图。
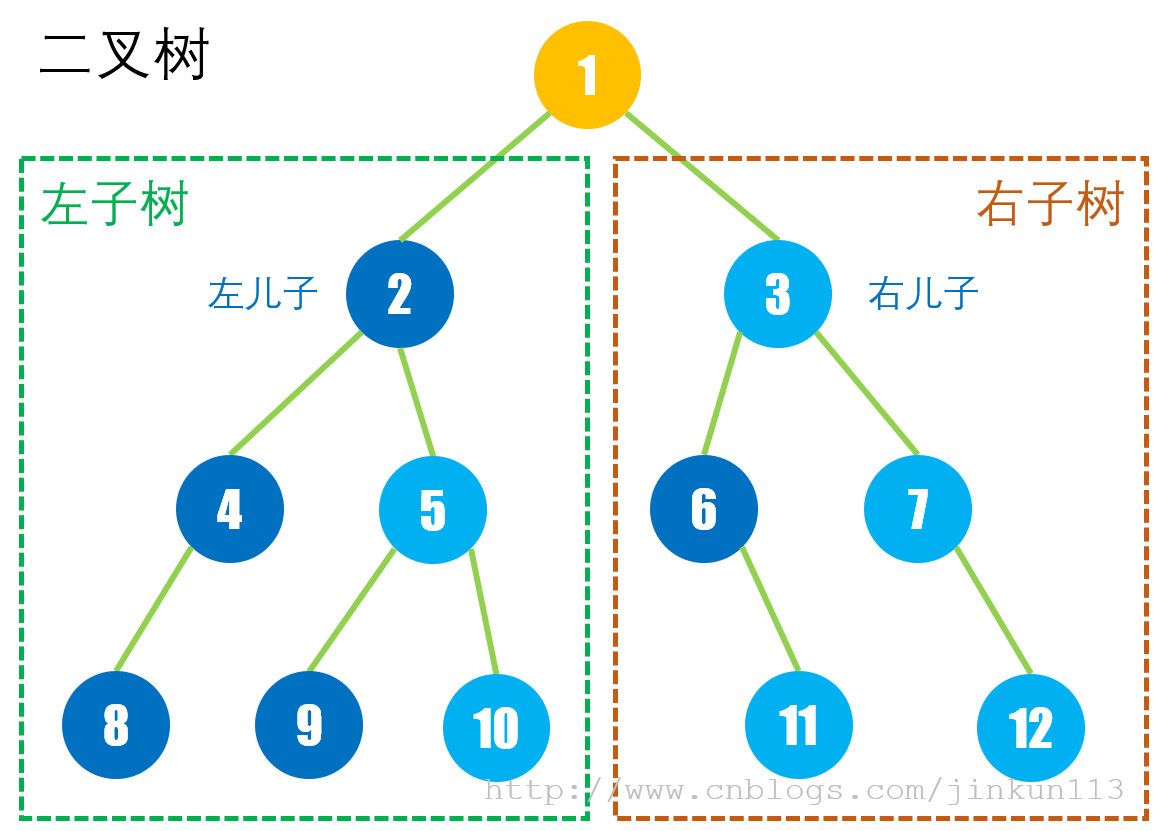
二叉树继承所有树结构的性质和术语,此外还有其独有的性质。
> 第 i 层至多有 2 ^ (i - 1) 个结点;
> 深度为 k 的二叉树至多有 2 ^ k - 1 个结点;
② 特殊二叉树
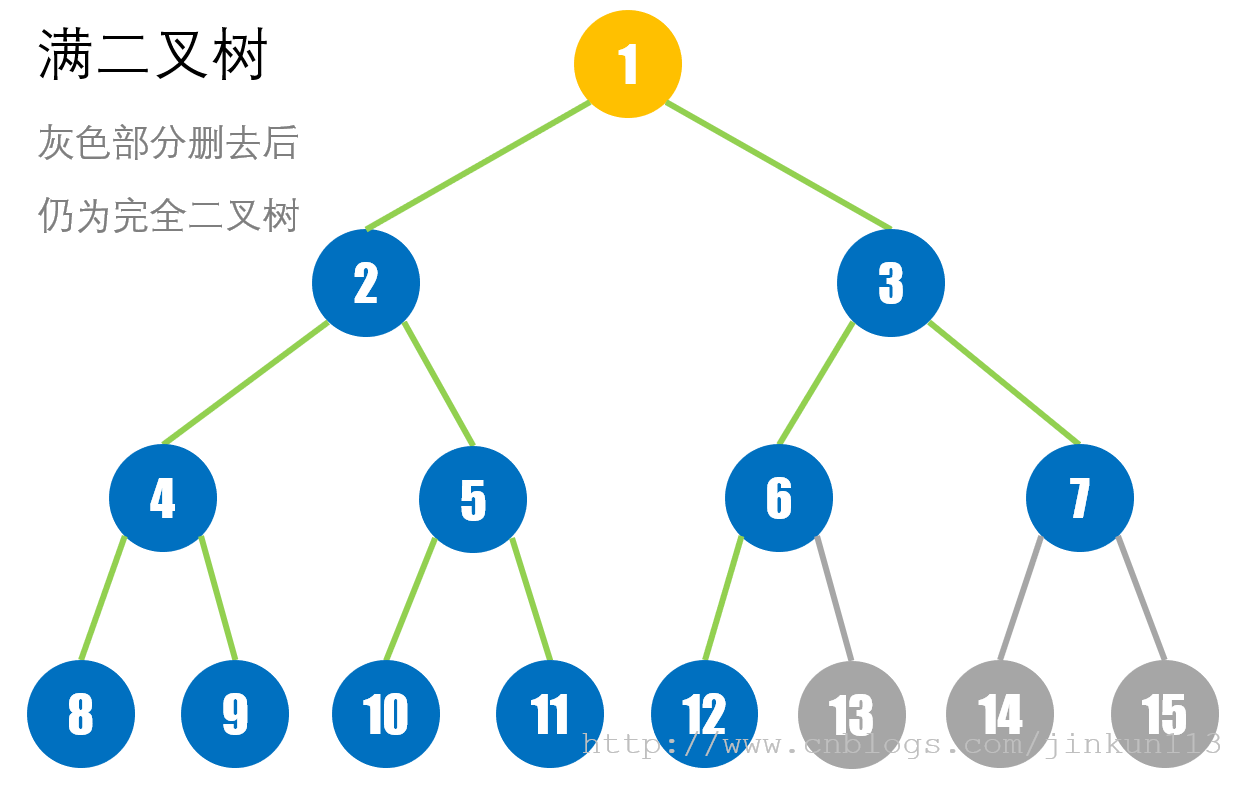
> 一棵深度为 k 且有 2 ^ k - 1 个结点的二叉树称为满二叉树。即除了叶子结点,所有结点都有 2 个儿子节点。
> 在满二叉树的基础上,允许叶子结点的父亲结点所属的层次没有叶子结点,即在深度最大和次大的部分才会出现叶子结点,而其他结点与满二叉树的编号保持一致,这样的二叉树称为完全二叉树。满二叉树是完全二叉树的一种。
见下图。
3、二叉树的存储
① 顺序存储结构
因为结构单一,完全二叉树可以考虑用顺序存储结构,即在数组中就能完成对二叉树的数据存储。假设读入二叉树数组 a[i],其第 i 位表示第 i 个结点,而由上图就可以看出,第 i 个结点的左儿子结点为 i * 2,右儿子结点为 i * 2 + 1。
线段树(请参见:<施工中>),堆(请参见:7.4 堆与优先队列)就属于完全二叉树的一种,一般采用顺序存储结构。
以上述的三层满二叉树为例,更形象地体现顺序存储结构:

而对于非完全二叉树,采用顺序存储结构可能会浪费大量空间,最坏的情况下,一个深度为 k 且只存在 k 个结点(即形成了一条线)的单支树却需要 2 ^ k - 1 的空间,这时候就需要链式存储结构。
② 链式存储结构
链表相比数组更擅长处理结点之间的关系,链式存储结构相比顺序存储结构也是如此。每一个结点数据由权值,左儿子指针和右儿子指针组成。有必要的话,还可以增加父亲指针,以便于向上寻找祖先。它适用于所有二叉树。
1 class Node { 2 int v; 3 Node* ls, rs, fa; 4 }; 5 6 class binaryTree { 7 Node a[MAXN]; 8 }
4、二叉树的遍历
① 先序,中序与后序
对于所有数据结构,遍历功能是不可少的 —— 遍历,按照某条搜索路径访问每个结点,使得每个结点被且仅被访问一次。由于结构非线性,树的遍历更为复杂,而因为二叉树的特殊结构,其遍历更为有规律可循。
回顾二叉树的定义,二叉树由三部分组成:根结点,左子树,右子树。遍历的过程和定义同理,也是通过递归完成,并且分成三种遍历方式:
> 先序遍历
对于任意一棵二叉树,先访问其根结点,再访问其左子树,最后访问其右子树。
举个例子:
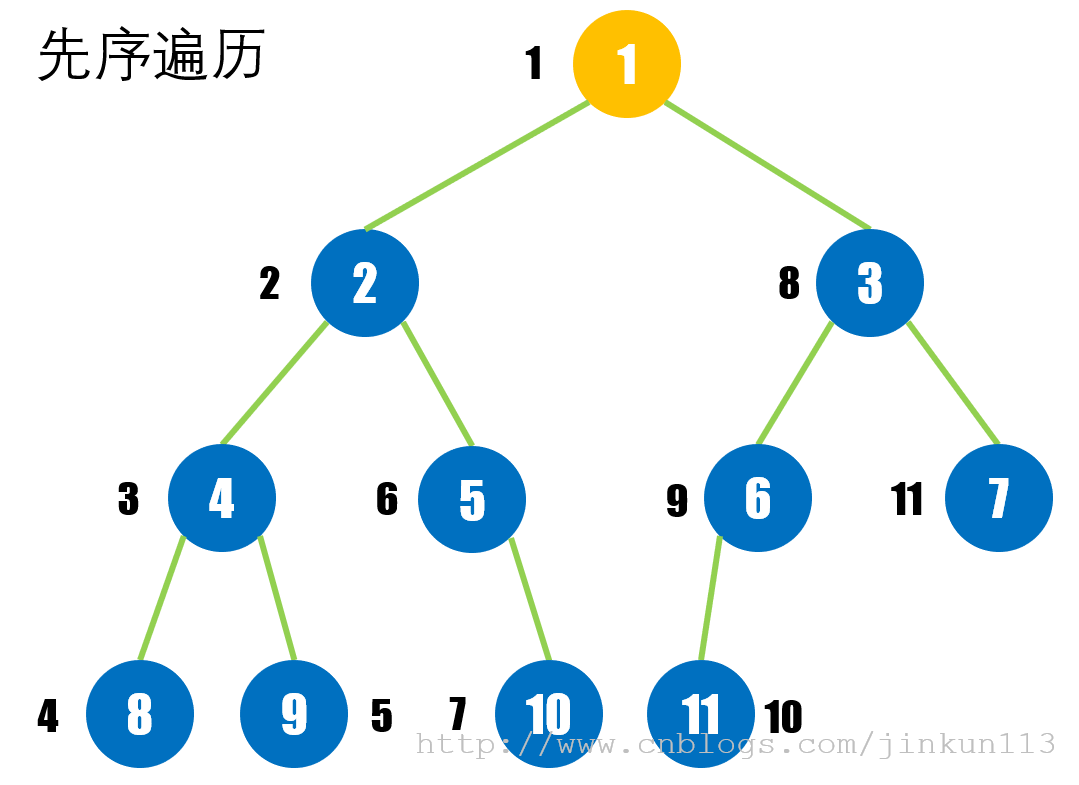
则先序遍历序列为:{1, 2, 4, 8, 9, 5, 10, 3, 6, 11, 7}
> 中序遍历
对于任意一棵二叉树,先访问其左子树,再访问其根结点,最后访问其右子树。
如图:
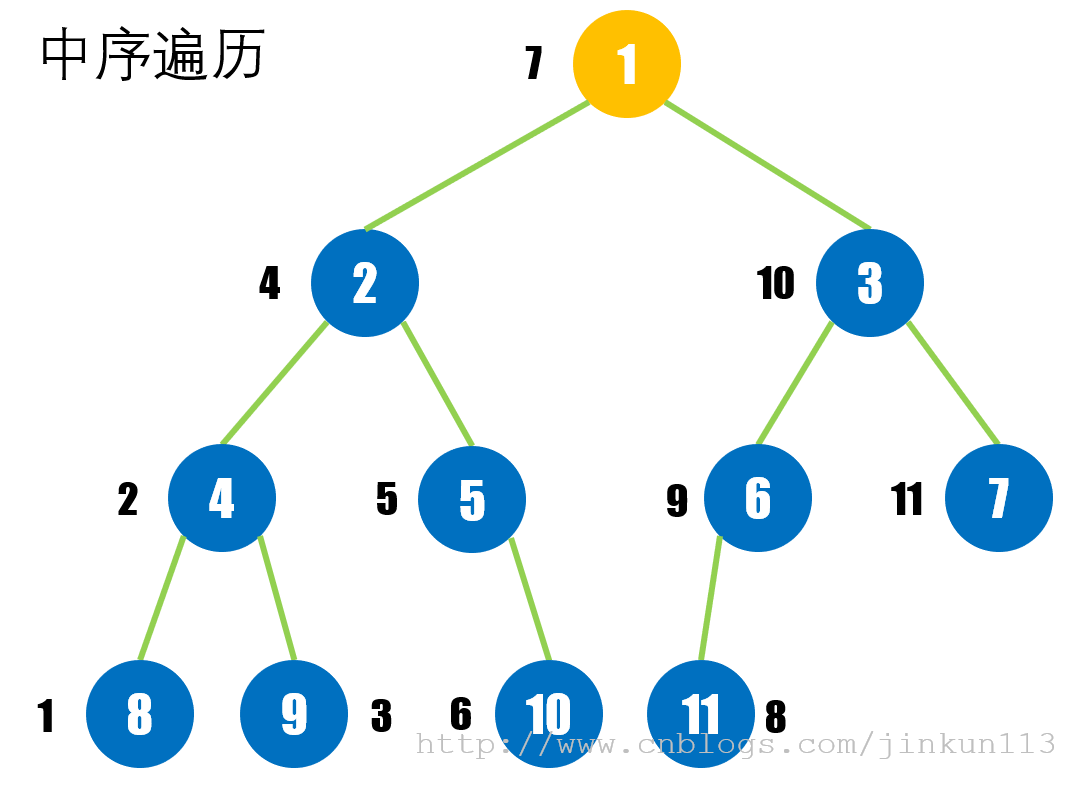
> 后序遍历
对于任意一棵二叉树,先访问其左子树,再访问其右子树,最后访问其根结点。
如图:
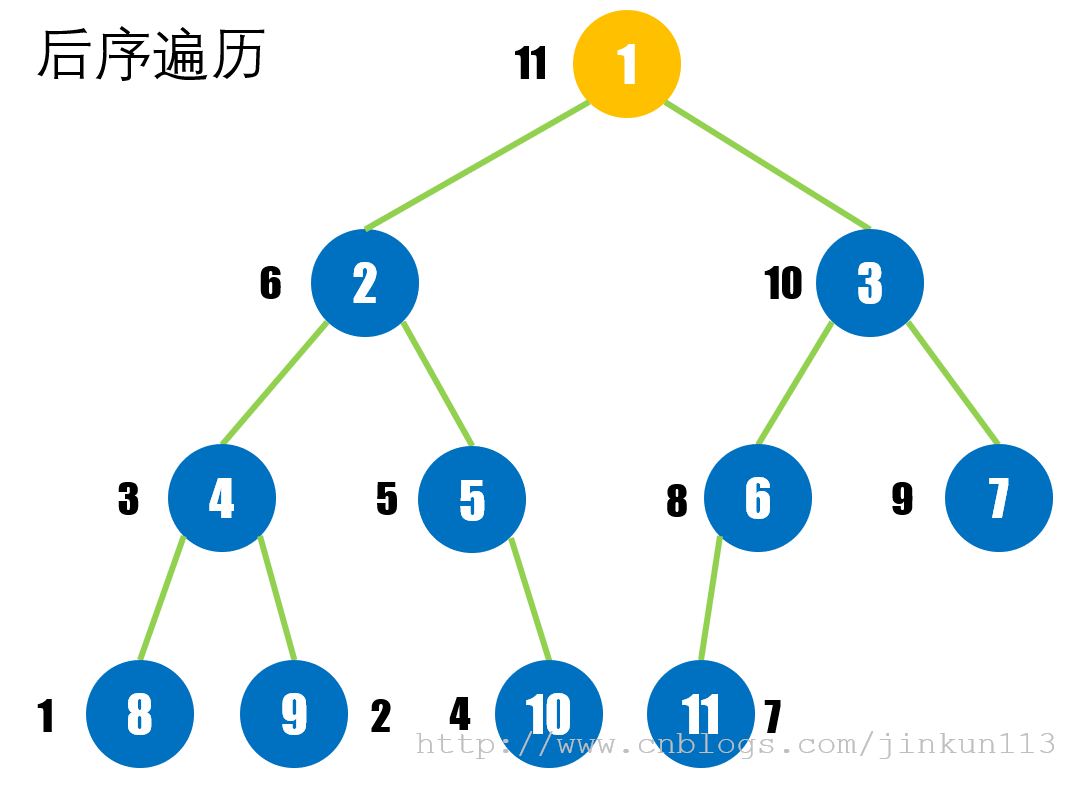
三种遍历得到的遍历序列,如果给出其中两种,可以得到第三种。具体步骤暂时省略。
② 表达式表示
将二叉树的权值改成变量和运算符,其中叶子结点为变量,非叶子结点为运算符,可以用来表示表达式。以二叉树表示表达式的递归定义如下:
假设表达式形式为:第一操作数 运算符 第二操作数,则其对应的二叉树中,左子树表示第一操作数,右子树表示第二操作数,树的根结点存放运算符。操作数可能是简单变量,也可能是表达式。
根据定义,表达式 (a * b + c) * (d / e - f) 的二叉树表示为:
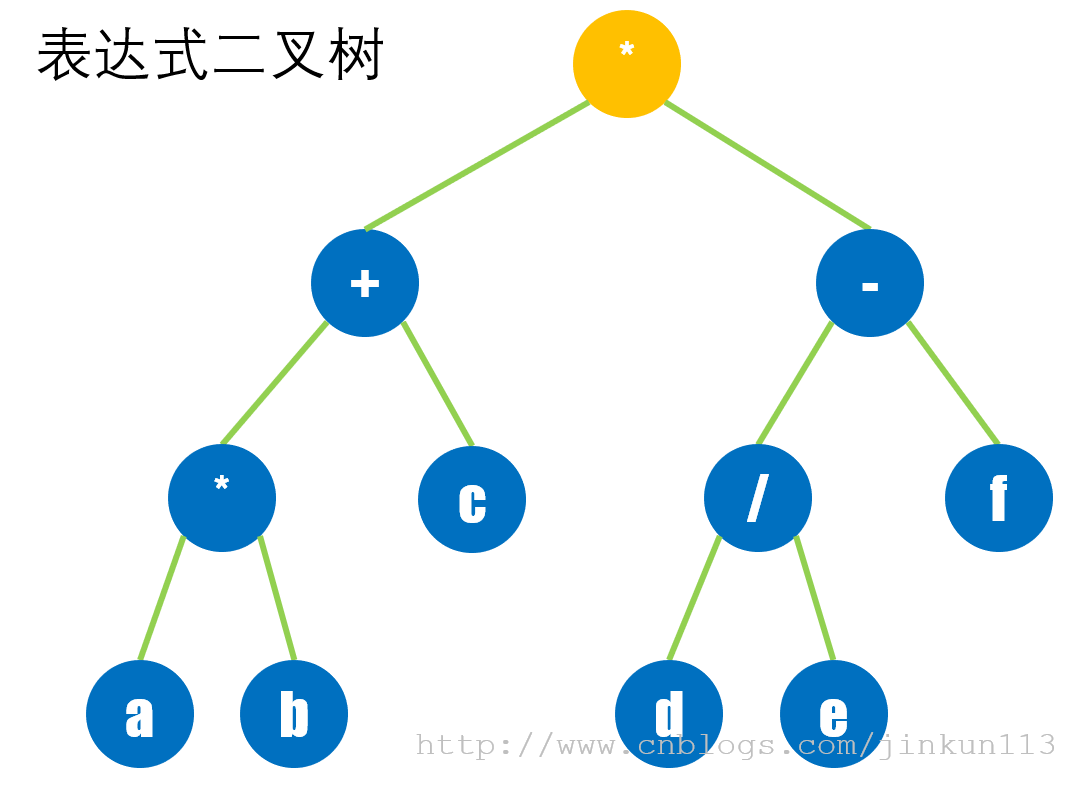
对这棵表达式二叉树分别进行三种遍历,得到的序列分别为:
先序遍历:*+*abc-/def(前缀表达式,波兰式)
中序遍历:a*b+c*d/e-f(中缀表达式)
后序遍历:ab*c+de/f-*(后缀表达式,逆波兰式)
三种表达式中,我们比较熟悉的是中缀表达式,即运算符放在操作数之间,但其实对于计算机,并不是一种合适的表达方式。可以看出我们给出的表达式和中缀表达式是有区别的 —— 中缀表达式没有括号,因为存在 * / 的优先级高于 + - 的问题,没有括号则意味着运算先后顺序是不同的。
但是,利用前缀和后缀表达式,计算机却能正确计算,计算过程略。
5、树的存储与遍历
将存储和遍历从二叉树扩展到树,又有什么不同?
① 树的存储
> 双亲表示法
对于每个结点,存储其权值和父亲结点指针,也就是说只能从下至上遍历。
> 孩子表示法
对于每个结点,存储其权值和所有儿子结点指针。不同于二叉树至多存在 2 个儿子,树的儿子结点个数不确定,故需要使用链表存储。也就是说只能从上至下遍历。
> 孩子兄弟(二叉链表)表示法
对于每个结点,存储其权值,大儿子结点指针和弟弟结点指针。树不一定是有序的,但是在读入时必然存在先后顺序,可以根据这个先后顺序来定义谁是大儿子,谁是谁的弟弟。
② 树的遍历
> 先序遍历
概念同二叉树,本质上是图论中的 DFS。
关于 DFS,请参见 3.1 DFS / BFS 搜索 和 8.2 图的存储与遍历。
> 后序遍历
概念同二叉树。
> 层次遍历
自上而下,自左而右访问每个结点,本质上是图论中的 BFS。
关于 BFS,请参见 3.1 DFS / BFS 搜索 和 8.2 图的存储与遍历 。
6、哈夫曼树
请参见:7.5 Huffman 哈夫曼树
7、树与图
关于图及其相关概念,请参见:8.1 图的简介与相关概念
其实将树归类于图论不无道理,如果已经了解了图是什么应该就知道,树本质上就是一种特殊的图。上面对树的介绍是以有根树为基础的,即规定了根结点,且有明确的单向父子关系。同理,还有一种无根树,没有固定结点,就可以完全认为是图了,并且存在一种等价的定义:由 n 个点,n - 1 条边组成的无向图。
所以在许多本质是树结构的题目中,一般并不会说是树,而是把其视作一种特殊的图,所以一旦题干声明了上述等价的定义,就可以认为是树了。
大多数情况下,对有根树的读入方式是给出“父亲-儿子”结点对,然后以图的方式进行存储。因为其相邻结点只有儿子结点和父亲结点两种情况,然后又给出了每个结点的父亲结点编号,所以遍历的时候进行一下特判就行了。
对无根树的读入方式则和图完全一样。




